Norm (mathematics)
![]()
This article is about norms in vector spaces, for norms in body theory see norm (body extension), for the norm of an ideal see ideal (ring theory).
In mathematics, a norm (from the Latin norma "guideline") is a mapping that assigns a number to a mathematical object, for example a vector, a matrix, a sequence or a function, that is intended to describe the size of the object in a certain way. The specific meaning of "magnitude" depends on the object under consideration and the norm used; for example, a norm may represent the length of a vector, the largest singular value of a matrix, the variation of a sequence, or the maximum of a function. A norm is symbolized by two vertical lines ‖ 
Formally, a norm is a mapping that associates a non-negative real number with an element of a vector space over the real or complex numbers and has the three properties of definiteness, absolute homogeneity, and subadditivity. A norm may (but need not) be derived from a scalar product. If a norm is assigned to a vector space, one obtains a normed space with important analytic properties, since every norm on a vector space also induces a metric and hence a topology. Two mutually equivalent norms induce the same topology, whereas on finite-dimensional vector spaces all norms are mutually equivalent.
Norms are studied in particular in linear algebra and functional analysis, but they also play an important role in numerical mathematics.
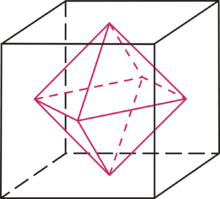
Sets of constant norm (norm spheres) of the maximum norm (cube surface) and the sum norm (octahedron surface) of vectors in three dimensions
Basic Terms
Definition
A norm is a mapping ‖ 




which for all vectors 

| (1) Definiteness: |
|
| (2) absolute homogeneity: |
|
| (3) Subadditivity or triangle inequality: |
|
Here 
This axiomatic definition of the norm was established by Stefan Banach in his 1922 dissertation. The standard symbol used today was first 


Example
The standard example of a norm is the Euclidean norm of a vector 


which corresponds to the descriptive length of the vector. For example, the Euclidean norm of the vector equal to

Basic properties
From the absolute homogeneity, by setting α follows 

thus the opposite direction of definiteness. Therefore, a vector has 


thus symmetry with respect to sign reversal. From the triangle inequality then follows by setting 
holds. Thus, every vector different from the zero vector has a positive norm. Furthermore, the inverse triangle inequality applies to norms

which can be shown by applying the triangle inequality to 
![t\in [0,1]](https://www.alegsaonline.com/image/31a5c18739ff04858eecc8fec2f53912c348e0e5.svg)

Standard balls
For a given vector 


or
open or closed norm sphere and the set
norm sphere around 






In any case, a norm sphere must be a convex set, otherwise the corresponding mapping would not satisfy the triangle inequality. Furthermore, a norm sphere must always be point symmetric with respect to 
Induced norms
→ Main article: Scalar product norm
A norm may, but need not necessarily, be 


i.e. the root of the scalar product of the vector with itself. In this case, one speaks of the norm induced by the scalar product or Hilbert norm. Every norm induced by a scalar product satisfies the Cauchy-Schwarz inequality
and is invariant under unitary transformations. According to the Jordan-von Neumann theorem, a norm is induced by a scalar product if and only if it satisfies the parallelogram equation. However, some important norms are not derived from a scalar product; in fact, historically, an essential step in the development of functional analysis was the introduction of norms not based on a scalar product. For every norm, however, there is an associated semi-inner product.
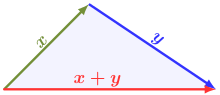
According to the triangle inequality, the length of the sum of two vectors is at most as great as the sum of their lengths; equality holds exactly when the vectors x and y point in the same direction.

Unit sphere (red) and sphere (blue) for the Euclidean norm in two dimensions
Norms on finite dimensional vector spaces
Number standards
Amount standard
→ Main article: Magnitude function
The magnitude of a real number 
The magnitude of a complex number 
where 



The absolute value norm is derived from the standard scalar product of two real or complex numbers
for 
induced.
Vector norms
In the following, real or complex vectors 





Maximum standard
→ Main article: Maximum standard
The maximum norm, Chebyshev norm or ∞-norm (infinity norm) of a vector is defined as
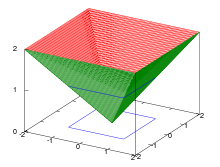
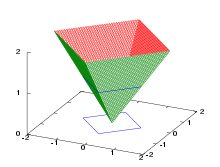
and corresponds to the magnitude of the largest component of the vector. The unit sphere of the real maximum norm has the shape of a square in two dimensions, the shape of a cube in three dimensions and the shape of a hypercube in general dimensions.
The maximum norm is not induced by a scalar product. The metric derived from it is called the maximum metric, Chebyshev metric, or, especially in two dimensions, the chessboard metric, since it measures the distance corresponding to the number of steps a king must take in chess to move from one square on the chessboard to another. For example, since the king can move diagonally, the distance between the centers of the two diagonally opposite corner squares of a chessboard in the maximum metric is equal to 
The maximum standard is a special case of the product standard
over the product space 




Euclidean norm
→ Main article: Euclidean norm
The Euclidean norm or 2-norm of a vector is defined as
and corresponds to the square root of the sum of the magnitude squares of the components of the vector. For real vectors, the magnitude dashes can be omitted in the definition, but not for complex vectors.
The unit sphere of the real Euclidean norm has the shape of a circle in two dimensions, the shape of a spherical surface in three dimensions and the shape of a sphere in general dimensions. In two and three dimensions, the Euclidean norm describes the descriptive length of a vector in the plane and in space, respectively. The Euclidean norm is the only vector norm that is invariant under unitary transformations, for example rotations of the vector around the zero point.
The Euclidean norm is given by the standard scalar product of two real or complex vectors 
resp
induced. A vector space provided with the Euclidean norm is called a Euclidean space. The metric derived from the Euclidean norm is called the Euclidean metric. For example, according to the Pythagorean theorem, the distance between the centers of the two diagonally opposite corner squares of a checkerboard in the Euclidean metric is equal to 
Sum standard
→ Main article: Sum standard
The sum norm, (more precisely) magnitude sum norm, or 1-norm (read: "one-norm") of a vector is defined as.
and corresponds to the sum of the magnitudes of the components of the vector. The unit sphere of the real sum norm has the shape of a square in two dimensions, an octahedron in three dimensions and a cross polytope in general dimensions.
The sum norm is not induced by a scalar product. The metric derived from the sum norm is also called the Manhattan metric or the taxi metric, especially in real two-dimensional space, because it measures the distance between two points like the driving distance on a grid-like city map on which one can only move in vertical and horizontal sections. For example, the distance between the centers of the two diagonally opposite corner squares of a checkerboard in the Manhattan metric is equal to 
p standards
→ Main article: p standard
In general, for real 

define. Thus, for 





All 


where in the case of the maximum norm the exponent 




Matrix standards
→ Main article: Matrix standard
In the following, we consider real or complex matrices 


with 
for all 
Matrix norms over vector norms
By writing all entries of a matrix one below the other, a matrix can also be viewed as a corresponding long vector of 


Where 
Matrix norms via operator norms
→ Main article: natural matrix norm
A matrix norm is called induced from a vector norm or natural matrix norm if it is derived as an operator norm, that is, if:

Descriptively, a matrix norm defined in this way corresponds to the largest possible stretching factor after applying the matrix to a vector. As operator norms, such matrix norms are always submultiplicative and compatible with the vector norm from which they were derived. In fact, among all matrix norms compatible with a vector norm, an operator norm is the one with the smallest value. Examples of matrix norms defined in this way are the row sum norm based on the maximum norm, the spectral norm based on the Euclidean norm, and the column sum norm based on the sum norm.
Matrix norms over singular values
Another way to derive matrix norms over vector norms is to consider a singular value decomposition of a matrix 









Examples of matrix norms defined in this way are the shadow norms defined over the 
absolute norm of a real number
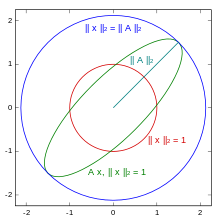
The spectral norm of a 2 × 2 matrix corresponds to the largest stretching of the unit circle by the matrix
Search within the encyclopedia