Newton's method

The Newton method, also Newton-Raphson method (named after Sir Isaac Newton 1669 and Joseph Raphson 1690), is a commonly used approximation algorithm in mathematics for the numerical solution of nonlinear equations and systems of equations. In the case of an equation with one variable, given a continuously differentiable function $f\colon \mathbb {R} \to \mathbb {R}$ Approximations to solutions of the equation f(x)=0 , i.e., find approximations of the zeros of this function. The basic idea of this procedure is to linearize the function in a starting point, i.e., to determine its tangent, and to use the zero of the tangent as an improved approximation of the zero of the function. The obtained approximation serves as a starting point for another improvement step. This iteration is done until the change in the approximate solution falls below a fixed bound. In the best case, the iteration procedure converges asymptotically with a quadratic order of convergence; the number of correct decimal places then doubles in each step.

Formally expressed, starting from an initial value $x_{0}$ the iteration

$x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}$

repeated until sufficient accuracy is achieved.

Newton method for real functions of a variable

Historical facts about the Newton method

Isaac Newton wrote in the period 1664 to 1671 the work "Methodus fluxionum et serierum infinitarum" (Latin for: Of the method of fluxions and infinite sequences). In it he explains a new algorithm for solving a polynomial equation using the example $y^{3}-2y-5=0$ . To do this, one can easily guess the point y=2 as a first approximation. Newton made the approximation y=2+p with assumed to be "small" and substituted this into the equation:

According to the binomial formulae

$y^{3}=(2+p)^{3}=8+12p+6p^{2}+p^{3}\$

$\ 2y=2(2+p)=4+2p$

$\Rightarrow \ 0=y^{3}-2y-5=-1+10p+6p^{2}+p^{3}$ .

Since is supposed to be "small", the higher order terms can be neglected with respect to the linear and constant ones, leaving 10p-1=0 or . p=0{,}1 We can now repeat this procedure and assume p=0{,}1+q , substitute into the second equation, omit higher terms and $q=-0{,}061/11{,}23=-0{,}0054\dots$ obtain

Joseph Raphson described this computational process formally in 1690 in the work "Analysis Aequationum universalis" and illustrated the formalism on the general equation of the third degree, finding the following iteration rule.

The abstract form of the method using the derivative $x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}$ comes from Thomas Simpson.

graph construction

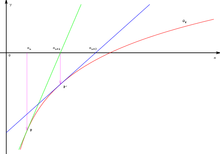
Descriptively, one arrives at this procedure as follows: Let $f\colon \mathbb {R} \to \mathbb {R}$ a continuously differentiable real function of which we know a point $x_{n}$ in the domain of definition with "small" function value. We want to $x_{n}$ find a point $x_{n+1}$ near that is an improved approximation of the zero. To do this, we linearize the function at the point , $x_{n}$ i.e., we replace it by its tangent at the point $P(x_{n}\,;\,f(x_{n}))$ with slope $f^{\prime }(x_{n})$ .

The tangent is $t(x_{n}+h):=f(x_{n})+f^{\prime }(x_{n})h$ given by the function Putting $h=x-x_{n}$ , we get.

$t(x):=f(x_{n})+f^{\prime }(x_{n})(x-x_{n})$ .

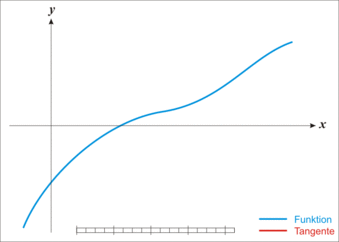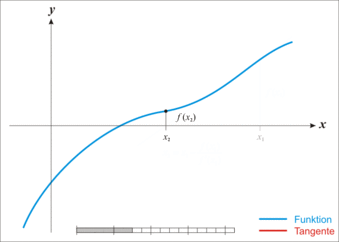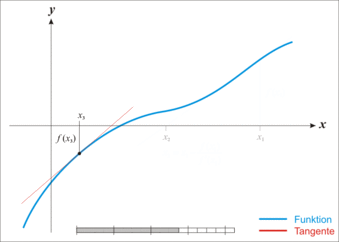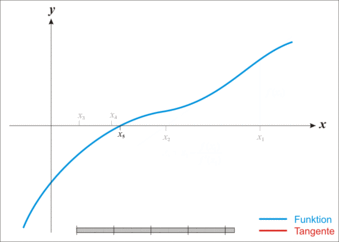
We choose as $x_{n+1}$ the single zero of this linear function,

$0=t(x_{n+1})=f(x_{n})+f^{\prime }(x_{n})(x_{n+1}-x_{n})\quad \Rightarrow \quad x_{n+1}=x_{n}-f(x_{n})/f'(x_{n})$ .

Applying this construction several times, we obtain from a first digit $x_{0}$ an infinite sequence of digits , which is $(x_{n})_{n\in \mathbb {N} }$ given by the recursion rule

$x_{n+1}:=N_{f}(x_{n}):=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}$

is defined. This prescription is also called Newton iteration, the function $N_{f}$ as Newton operator. Newton iteration is a special case of fixed point iteration if the sequence $\xi =\lim _{n\to \infty }x_{n}\,$ converges to ξ so ξ $\xi =N_{f}(\xi )=\xi -f(\xi )/f'(\xi )$ and therefore $f(\xi )=0$ .

The art of using Newton's method is to find suitable initial values . The $x_{0}$ more is known about the function , the smaller the necessary set of initial values can be designed.

Many nonlinear equations have multiple solutions, so a polynomial of -th degree has up to zeros. If one wants to find all zeros in a given domain $D\subseteq \mathbb {R}$ , then for each zero a suitable initial value in must be found for which the Newton iteration converges. To do this, one could, for example, determine sufficiently small isolating intervals to each zero by bisection.

First example

The square root of a number a>0 is the positive zero of the function $f(x)=1-a/x^{2}$ . This function has derivative $f^{\prime }(x)=2a/x^{3}$ , so the Newton iteration is done according to the rule.

$x_{n+1}:=N_{f}(x_{n})=x_{n}-{\frac {1-a/x_{n}^{2}}{2a/x_{n}^{3}}}=x_{n}-{\frac {x_{n}^{3}}{2a}}+{\frac {x_{n}}{2}}={\frac {x_{n}}{2}}\left(3-{\frac {x_{n}^{2}}{a}}\right)$

The advantage of this rule over Heron's root extraction (see below) is that it is division-free once the reciprocal of been determined. The starting value $x_{0}:=(1+a)/2$ chosen in the table was The iterates were truncated at the first imprecise location. It can be seen that after a few steps, the number of valid digits grows rapidly.

n	$x_{n}$ at	$x_{n}$ at	$x_{n}$ at
0
1
2
3
4
5
6
7
8

If we consider the difference $x_{n+1}-{\sqrt {a}}$ to the limit in the (n+1) -th step, then using the binomial formulas, the difference in the -th step can be split off twice:

$x_{n+1}-{\sqrt {a}}={\frac {3}{2}}x_{n}-{\frac {x_{n}^{3}}{2a}}-{\frac {3}{2}}{\sqrt {a}}+{\frac {{\sqrt {a}}^{3}}{2a}}=(x_{n}-{\sqrt {a}})\cdot \left({\frac {3}{2}}-{\frac {x_{n}^{2}+x_{n}{\sqrt {a}}+a}{2a}}\right)$

$=(x_{n}-{\sqrt {a}})\cdot {\frac {a-x_{n}^{2}+a-x_{n}{\sqrt {a}}}{2a}}=-(x_{n}-{\sqrt {a}})^{2}\cdot {\frac {x_{n}+2{\sqrt {a}}}{2a}}$

According to the inequality from the arithmetic and geometric mean, $0<{\sqrt {a}}\leq {\frac {1+a}{2}}$ , so the second factor can be usefully 3/2(1+a) constrained by If the difference in the -th step is a small number, the difference in the (n+1) -th step is proportional to the square of it, so it is much smaller. Thus, squaring an error $10^{{-m}}$ gives an error estimate proportional to $10^{{-2m}}$ . Therefore, the number of valid digits is said to approximately double in each step of Newton iteration.

Animation: Iteration with the Newtonian method

Convergence Considerations

The Newton method is a so-called locally convergent method. Convergence of the sequence generated in the Newton iteration to a zero is therefore only guaranteed if the starting value, i.e. the 0-th member of the sequence, is already "sufficiently close" to the zero. If the starting value is too far away, the convergence behavior is not fixed, i.e., both a divergence of the sequence and an oscillation (in which finitely many function values alternate) or a convergence to another zero of the function under consideration are possible.

If the starting value $x_{0}$ is chosen in such a way that the Newton method converges, then the convergence is quadratic, however, i.e. with the order of convergence 2 (if the derivative does not vanish at the zero point). The set of starting points for which the Newton method converges to a certain zero forms the catchment area of this zero. If you color the catchment areas of different zeros in the complex plane differently for a polynomial function with real or complex coefficients, you get a Newton fractal. In this fractal it can be seen that the catchment areas contain basins, i.e. circular disks around the zeros, from which the Newton iteration converges stably towards the zero in the centre. But it can also be seen that the edges of the catchment areas are "frayed", they even have a fractal structure. So small deviations in the starting point can lead to different zeros.

However, if there is $I={]a,b[}$ exactly one zero in the interval , in consistently $f'>0$ as well as $f''<0$ holds and the initial value $\xi \in I$ chosen to $x_{0}\in I$ the left of the zero ξ, then the sequence always converges in Newton's method, strictly monotonically increasing (see the figure below resp. the table above from n=1 ).

Examples of non-convergence

Oscillatory behavior results, among others, for the polynomial $f(x):=x^{3}-2x+2$ with $f^{\prime }(x)=3x^{2}-2$ . The point with and f^{\prime $f^{\prime }(0)=-2$ is mapped by the Newton operator to the point the point in turn, with and $f^{\prime }(1)=1$ , is mapped to , so Newton iteration with one of these points as the initial value yields a periodic sequence, these two points alternate cyclically. This cycle is stable, it forms an attractor of the Newton iteration. This means that there are environments around both points, so that starting points from these environments converge against the cycle and thus have one each of the points 0 and 1 as the limit of the subsequence with even index and that with odd index.
Divergence or arbitrary distance from the starting point results for $f(x)=\sin(x)$ with $f^{\prime }(x)=\cos(x)$ and $N(x)=x-\tan(x)$ . There exists a place $x_{0}\in \lbrack -\pi /2,0\rbrack$ with $\tan(x_{0})=-2\pi$ i.e. $x_{0}=\arctan(-2\pi )=-1{,}412965136506737759\dots$ One convinces oneself that then $x_{n}=x_{0}+2\pi n$ holds. This behavior is not stable, because when the initial value is slightly varied, such as by numerical computation, the Newton iteration moves further and further away from the ideal divergent sequence. Even with eventual convergence, the zero found will be very far from the initial value.

Local quadratic convergence

Let be a twice continuously differentiable real function and a simple zero of , in which the derivative thus has no zero. This means that the graph of the function is transversal, i.e. non-touching, intersecting the axis. Let be a point close to . Then the second degree Taylor formula (with Lagrangian remainder) can be

$0=f(a)=f(x)+f'(x)(a-x)+{\tfrac {1}{2}}f''(\xi )(a-x)^{2},\qquad \xi$ lies between and ,

(x-a) can be rearranged according to the difference

$x-a={\frac {f(x)}{f'(x)}}+{\frac {f''(\xi )}{2\,f'(x)}}(x-a)^{2}$ .

It is now rearranged so that the Newton operator appears on the right-hand side,

$N_{f}(x)-a=x-{\frac {f(x)}{f'(x)}}-a={\frac {f''(\xi )}{2\,f'(x)}}(x-a)^{2}$ .

Let be an interval around without zero of the derivative f'(x) and $m_{1}=\min _{x\in I}|f'(x)|$ and $M_{2}=\max _{x\in I}|f''(x)|$ bounds on the derivatives of . Then for all $x\in I$ the estimation follows

${\Bigl |}N_{f}(x)-a{\Bigr |}\leq {\frac {M_{2}}{2m_{1}}}|x-a|^{2}$ .

Let $K={\tfrac {M_{2}}{2m_{1}}}$ denote the constant factor. At each step the Newton iteration, the quantity $d_{n}=K\,|x_{n}-a|$ be smaller than the square of the same magnitude in the previous step, $d_{n}\leq K\cdot K|x_{n-1}-a|^{2}=d_{n-1}^{2}$ . After complete induction we get

$K\,|x_{n}-a|=d_{n}\leq d_{n-1}^{2}\leq d_{n-2}^{4}\leq \dotsb \leq d_{0}^{2^{n}}=(K\,|x_{0}-a|)^{2^{n}}$ .

Thus, if the starting point of the iteration can be guaranteed to be the estimate $|x_{0}-a|<{\tfrac {1}{K}}$ , e.g. by the interval length of being less than 1/K , then the sequence $(x_{n})$ of Newton iteration converges to the zero , because the sequence $(d_{n})_{n\in \mathbb {N} }$ and hence $(x_{n}={\tfrac {1}{K}}d_{n})_{n\in \mathbb {N} }$ is a zero sequence according to the given estimation. The shortening of the interval can be achieved by some iterations of a slower procedure for zero constraint, e.g., the bisection procedure or the regula falsi.

The convergence rate following from these estimates is called quadratic, the (logarithmic) precision or number of valid digits doubles in each step. The estimation of the distance $|x_{n}-a|$ to the zero is often given linearly in $|x_{0}-a|$ , e.g. the following holds

$|x_{n}-a|\leq \left({\tfrac {1}{2}}\right)^{2^{n}-1}\cdot |x_{0}-a|$ , if the length of the interval is less than ${\tfrac {1}{2K}}$ This gives an estimate of the valid digits in the binary system.
$|x_{n}-a|\leq \left({\tfrac {1}{10}}\right)^{2^{n}-1}\cdot |x_{0}-a|$ , if the length of the interval is less than ${\tfrac {1}{10K}}$ , i.e., close enough to zero results in a doubling of the valid decimal places in each step.

Local quadratic convergence with multiple zeros by modification

In the case that has a multiple zero of finite degree at , the rate of convergence can also be estimated and quadratic convergence can be enforced again by a slight modification.

If has a -fold zero, be written as $f(x)=(x-a)^{k}\cdot g(x)$ with $g(a)\neq 0$ .

Then by the product rule $f'(x)=k\cdot (x-a)^{k-1}\cdot g(x)+(x-a)^{k}\cdot g'(x)$ and hence the expression

${\frac {f(x)}{f'(x)}}={\frac {(x-a)^{k}\cdot g(x)}{k\cdot (x-a)^{k-1}\cdot g(x)+(x-a)^{k}\cdot g'(x)}}=(x-a){\frac {g(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}$ .

If we now insert this into the iteration, we get

$x_{\text{neu}}=x-{\frac {f(x)}{f'(x)}}=x-(x-a){\frac {g(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}$

and from it, after bilateral subtraction of , the iteration error

$(x_{\text{neu}}-a)=(x-a)-(x-a){\frac {g(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}=(x-a)\left[1-{\frac {g(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}\right]$ . (*)

Now when the expression (x-a) become very small, the summand $(x-a)\cdot g'(x)$ in the denominator becomes much smaller than $k\cdot g(x)$ , so that the back bracket in approaches (*) more and more the value $s=1-{\tfrac {1}{k}}$ . For the simple zero with k=1 , one has a small value , which becomes almost 0 so that $(x_{\text{neu}}-a)=(x-a)\cdot s$ . For k=2 , becomes about 0.5, so the distance to zero only about halves from step to step, and after about 10 steps one has increased the precision only in another three decimal places. For k=3 , becomes about 0.67, so that only after about 16 steps the accuracy increases by another three decimal places, and so on.

Therefore one can estimate the multiplicity of the zero by the convergence behaviour, if one does not know it for other reasons, and - as now still described - optimize the procedure.

For a -fold zero one modifies the Newtonian approximation method with a factor :

$x_{\text{neu}}=x-k\cdot {\frac {f(x)}{f'(x)}}$ (Newton method with -fold zero).

Thus (*) then becomes.

${\begin{aligned}(x_{\text{neu}}-a)&=(x-a)\left[1-{\frac {k\cdot g(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}\right]\\&=(x-a)\left[{\frac {k\cdot g(x)+(x-a)\cdot g'(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}-{\frac {k\cdot g(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}\right]\\&=(x-a){\frac {(x-a)\cdot g'(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}\\&=(x-a)^{2}{\frac {g'(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}\end{aligned}}$

Now if (x-a) again very small, then in the denominator the summand becomes $(x-a)\cdot g'(x)$ much smaller than $k\cdot g(x)$ , and one obtains

$(x_{\text{neu}}-a)=(x-a)^{2}{\frac {g'(x)}{k\cdot g(x)}}$ ,

where the right factor converges to a fixed value because of $g(a)\neq 0$ . As can be seen, quadratic convergence is now also present here.

An example shows the convergence behavior very nicely. The function $f(x)=x^{2}-2$ has the simple zero ${\sqrt {2}}$ . The left column of the table shows the rapid convergence for the starting value 1, after 4 steps the precision cannot be increased any more, at the error the number of zeros behind the decimal point doubles (at least). If we now square the function (middle column), the zero becomes a double one, and now we see the behavior explained above, that without modification the error is only about halved in each step. If we then modify this case with the factor k=2 the same behavior as for the simple zero occurs (right column).

n	$x_{n}$ for $f(x)=x^{2}-2$	Error	$x_{n}$ for $f(x)=(x^{2}-2)^{2}$ without factor	Error	$x_{n}$ for $f(x)=(x^{2}-2)^{2}$ with factor	Error
0
1
2
3
4		$0$				$0$
5		$0$				$0$
6		$0$				$0$
7		$0$				$0$
8		$0$				$0$
9		$0$				$0$
10		$0$				$0$

The Newton method for complex numbers

For complex numbers complex one writes the formula accordingly:

$(1)\,z_{1}=z_{0}-{\frac {f(z_{0})}{f\,'\,(z_{0})}}$

with the holomorphic function $f(z),\,z=x+iy,\,i^{2}=-1,\;x,y\in \mathbb {R}$ . The decomposition into real and imaginary part gives

$f(z)=u(x,y)+iv(x,y)$

The complex derivative is independent of the direction of the derivative at the point z i.e. it is valid

${\frac {d}{dz}}f(z)\;=\;{\frac {\partial }{\partial x}}f(z)\;=\;{\frac {\partial }{\partial \,(iy)}}f(z)\;=\;{\frac {\partial }{i\,\partial \,y}}\,f(z)$

Therefore the Cauchy-Riemann differential equations are valid

$(2)\,u_{x}=v_{y}$ and $v_{x}=-u_{y}.$

The complex equation (1) can be decomposed into real and imaginary parts:

$(3)\,{\frac {f(z)}{f\,'(z)}}\,=\,{\frac {f(z)\cdot {\overline {\,f\,'(z)}}}{f\,'(z)\,\cdot {\overline {f\,'(z)}}}}\,=\,{\frac {(u+iv)\cdot (u_{x}-iv_{x})}{u_{x}^{2}+v_{x}^{2}}}$ .

With the help of (2) it follows

${\frac {f(z)}{f\,'(z)}}\,={\frac {1}{u_{x}^{2}+v_{x}^{2}}}\cdot \left\{\left(u\cdot u_{x}+v\cdot v_{x}\right)+i\left(u\cdot u_{y}+v\cdot v_{x}\right)\right\}$

The geometric meaning of this equation is seen as follows. One determines the minimum of the magnitude $\vert f(z)\vert$ . The minimum is assumed to be . $f(z)=0$ This can be determined using the gradient method, i.e., the steepest descent method.

One introduces the term $b(x,y)=\vert f(z)\vert ={\sqrt {u^{2}\,+\,v^{2}}}$ Using the vector formula for this method is ${\vec {x}}\,=\left({\begin{array}{*{20}c}{x}\\{y}\\\end{array}}\right)$ :

$(4)\,{\vec {x}}_{1}\;=\;{\vec {x}}_{0}\;-\;{\frac {b(x_{0},y_{0})}{\left|\,-\nabla \,b(x_{0},y_{0})\right|^{2}}}\cdot -\nabla \,b(x_{0},y_{0}).$

This is identical to formula (1).

Comments

The local convergence proof can also be done in the same way in the multidimensional case, but it is then technically a bit more difficult since two- and three-level tensors are used for the first and second derivatives, respectively. Essentially, the constant K is given by $K={\tfrac {1}{2}}\,\sup _{x\in U}\|f'(x)^{-1}\|_{(1,1)}\,\sup _{x\in U}\|f''(x)\|_{(1,2)}$ be replaced with appropriate induced operator norms.
The local convergence proof assumes that an interval containing a zero is known. From his proof, however, there is no way to test this quickly. A proof of convergence which also provides a criterion for this was first given by Leonid Kantorovich and is known as Kantorovich's theorem.
To find a suitable starting point, one sometimes uses other ("coarser") methods. For example, one can determine an approximate solution with the gradient method and then refine it with the Newton method.
If the starting point is unknown, one can use a homotopy to deform the function of which one is looking for a zero, to a simpler function of which (at least) one zero is known. One then runs through the deformation backwards in the form of a finite sequence of only "slightly" differing functions. From the first function one knows one zero. As starting value of the Newton iteration to the just current function of the sequence one uses the approximation of a zero of the function preceding in the sequence. For the exact procedure see homotopy method.

As an example may serve the "flooding homotopy": with an arbitrary we form the initial function $g(x)=f_{0}(x):=f(x)-f(z)$ with known zero . We have f(z) flooded the "water level" from the "zero level" to the level Now we gradually lower the water level, $f_{n}(x):=f(x)-(f(z)-n\cdot h\cdot f(z))$ , h=1/N , $n=1\dots N$ . At each step, an approximation ξ $\xi ^{(n)}$ of a zero is determined, where $x_{0}:=\xi ^{(n-1)}$ set. It is $f_{N}=f$ and hence ξ $\xi ^{(N)}$ one of the approximate solutions we are looking for.

The Newtonian approximation method .

Newton's method for the polynomial $z^{3}-1$ over the complex numbers converges to one of the three zeros of the polynomial for starting values from the red, the green and the blue regions, respectively. For initial values from the light structure, the Newton fractal, the method does not converge.

Dynamics of Newton's method for the function $x^{3}-2x+2$ with starting values between -4 and 4: Each color-coded line shows the result of one step of the method, applied to the line above. The initial values are in the top row. Many initial values converge to the (only real-valued) zero of the polynomial at about -1.769, whose color is middle blue. However, there are also many initial values for which the method does not converge and oscillates between zero (black) and one (red). The set of these starting values that do not lead to zero contains open intervals, i.e. it is a set of positive measure and thus in particular not a zero set.

Questions and Answers

Q: What is Newton's method?

A: Newton's method is an algorithm for finding the real zeros of a function. It uses the derivative of the function to calculate its roots, and requires an initial guess value for the location of the zero.

Q: Who developed this method?

A: The method was developed by Sir Isaac Newton and Joseph Raphson, hence it is sometimes called the Newton–Raphson method.

Q: How does this algorithm work?

A: This algorithm works by repeatedly applying a formula which takes in an initial guess value (xn) and calculates a new guess (xn+1). By repeating this process, the guesses will approach a zero of the function.

Q: What is required to use this algorithm?

A: To use this algorithm, you must have an initial "guess value" for the location of the zero as well as knowledge about the derivative of your given function.

Q: How can we explain Newton's Method graphically?

A: We can explain Newton's Method graphically by looking at intersections between tangent lines with x-axis. First, a line tangent to f at xn is calculated. Next, we find intersection between this tangent line and x-axis and record its x-position as our next guess - xn+1.

Q: Is there any limitation when using Newton's Method?

A: Yes, if your initial guess value is too far away from actual root then it may take longer time or even fail to converge towards root due to oscillations around it or divergence away from it.