Mutual information

Transinformation or mutual information is a quantity from information theory that indicates the strength of the statistical correlation between two random variables. The transinformation is also called synentropy. In contrast to the synentropy of a first-order Markov source, which expresses the redundancy of a source and should therefore be minimal, the synentropy of a channel represents the average information content that reaches the receiver from the sender and should therefore be maximal.

Occasionally, the term relative entropy is also used, but this corresponds to the Kullback-Leibler divergence.

The transinformation is closely related to the entropy and the conditional entropy. Thus, the transinformation calculated as I(X;Y) follows:

Definition about the difference of source entropy and equivocation or receiving entropy and misinformation:

$I(X;Y)=H(X)-H(X\vert Y)=H(Y)-H(Y\vert X).$

Definition about probabilities:

$I(X;Y)=\sum _{{x}}{}\sum _{{y}}{}p(x,y)\cdot \log _{2}\left({\frac {p(x,y)}{p(x)p(y)}}\right).$

Definition via the Kullback-Leibler divergence:

$I(X;Y)=D(p(x,y)\|p(x)p(y)).$

Definition about the expected value:

$I(X;Y)=E\left\{\log _{2}\left({\frac {p(x,y)}{p(x)p(y)}}\right)\right\}.$

If the transinformation disappears, one speaks of statistical independence of the two random variables. The transinformation becomes maximum if one random variable can be calculated completely from the other.

Transinformation is based on the definition of information introduced by Claude Shannon using entropy (uncertainty, mean information content). If the transinformation increases, the uncertainty about one random variable decreases under the condition that the other is known. Consequently, if the transinformation is maximal, the uncertainty vanishes. As can be seen from the formal definition, the uncertainty of one random variable is reduced by knowledge of another. This is expressed in the transinformation.

Transinformation plays a role in data transmission, for example. It can be used to determine the channel capacity of a channel.

Accordingly, an entropy H(Z) can also depend on two different, again interdependent, entropies:

Different terms are used in the literature. Equivocation is also called "loss entropy" and misinformation is also called "irrelevance". The transinformation is also called "transmission" or "mean transinformation content".

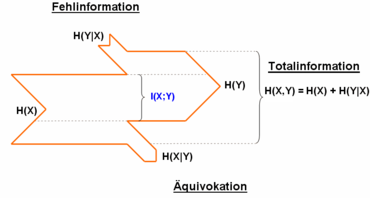
A memoryless channel connects the two sources X and Y. Transinformation flows from X to Y. The receiver source Y of the sender source X behaves like a source. No distinction is made between receiver and sender. The more the sources depend on each other, the more transinformation is present.

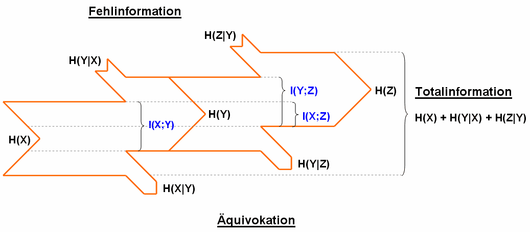
Two memoryless channels connect three sources. From the sender source X a transinformation of I(x;y) can be transmitted to the receiver source Y. If this transinformation is forwarded, the receiver source Z receives a transinformation of I(X;Z). One can see here clearly that the transinformation depends on the amount of equivocation.

Questions and Answers

Q: What is meant by mutual information?

A: Mutual information is a measure of how much more is known about one random value when given another.

Q: Can you give an example of how mutual information works?

A: Yes, for example, knowing the temperature of a random day of the year will not reveal what month it is, but it will give some hint, which is measured by mutual information.

Q: Does knowing what month it is reveal the exact temperature?

A: No, knowing what month it is will not reveal the exact temperature, but it can make certain temperatures more or less likely.

Q: What are the hints or changes in likelihood explained by?

A: The hints or changes in likelihood are explained and measured with mutual information.

Q: Can mutual information be used to measure other relationships between random values?

A: Yes, mutual information can be used to measure other relationships between random values.

Q: What is the practical use of mutual information?

A: The practical use of mutual information is in data analysis, where it can help identify important factors or variables that are related to each other.

Q: Is mutual information applicable only in data analysis or can it be used in other areas?

A: Mutual information can be used in various fields such as engineering, statistics, computer science, and machine learning, in addition to data analysis.