Monty Hall problem
![]()
This article is about the goat problem in probability theory. For the tethered goat problem, see Goat problem (geometry).
The Goat Problem, Three Door Problem, Monty Hall Problem, or Monty Hall Dilemma is a probability theory problem. The question is whether a choice, initially made at random among three a priori equally probable possibilities, should be changed when additional information is given.
The task is similar to the game show Let's Make a Deal hosted by Monty Hall, which became known in the German-speaking world in the variant Geh aufs Ganze! Two names mentioned above refer to the problem formulation, in which goats await the decision maker as consolation prizes behind two of three doors, if he has not chosen that door which stands for the main prize, a car.
Various understandings of the goat problem are often used as examples of how the human mind is prone to fallacies when it comes to determining probabilities, and have been the subject of long-running public debate.
The problem was posed by the biostatistician Steve Selvin, who presented it in a letter to the editor in the American Statistician in 1975. The problem became known to wider circles and the subject of controversial debate in 1990 through publication in Marilyn vos Savant's column "Ask Marilyn" in Parade magazine. This version was based on a letter to the editor that vos Savant had received from Craig F. Whitaker of Columbia, Maryland:
"Suppose you were on a game show and had a choice of three gates. Behind one of the gates is a car, behind the others are goats. You choose a gate, say gate number 1, and the emcee, who knows what is behind the gates, opens another gate, say number 3, behind which is a goat. He now asks you, 'Would you like gate number 2?' Is there any advantage in changing your choice of gate?"
The question in this form is underdetermined; the correct answer depends on what additional assumptions are made. Vos Savant gave the answer, "Yes, you should switch. The first gate chosen has a 1⁄3 chance of winning, but the second gate has a 2⁄3 chance of winning." Vos Savant's answer is correct, but only under the additional assumption that whether the car or a goat is behind the gate initially chosen by the contestant, the showmaster must open an unchosen gate with a goat and offer the switch in either case. Even under this additional assumption, it is counterintuitive to many people that the chance of winning actually increases to 2⁄3 instead of merely 1⁄2. As a result, by her own estimate, vos Savant received ten thousand letters, the vast majority of which doubted the accuracy of her answer.
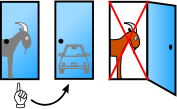
Hoping to win the car, the contestant chooses gate 1. The showmaster then opens gate 3, behind which is a goat, and offers the contestant to change gates. Is it advantageous for the candidate to change his first choice and choose gate 2?
The experiential response
If you ask the question to people who had not yet dealt with the problem, they often assume that the chances of winning for gates 1 and 2 are the same. The reason often given for this is that nothing is known about the motivation of the showmaster to open gate 3 with a goat behind it and to offer a change. Therefore, the indifference principle applies.
Intuition in understanding the letter to the editor assumes that the problem statement is a description of a unique game situation. In addition, the response evidences some familiarity with game shows such as Go for it, in which the showmaster (host) plays an active and unpredictable role. In contrast to the problem variants in which the presenter is reduced to a 'stooge' bound by fixed rules of behaviour, it may be realistically assumed that he is completely free to make his own decisions (Monty Hall: "I'm the man of the house!"). This freedom can be illustrated by a few examples, where before each game the car and goats were randomly redistributed behind the three gates. Because the candidates are familiar with this game show, for which they have applied as participants, they are naturally aware of the unpredictability of the host.
Game 1
Candidate Alfred chooses gate 1, the moderator opens gate 1 with a goat behind it; Alfred loses.
Game 2
Candidate Berta chooses gate 1, the presenter opens gate 2 with a goat behind it and offers Berta to change her choice. Berta wants to change, but the moderator does not open a gate, but offers 5000 euros for Berta to stay with her first choice. Berta does not change her choice and the moderator opens gate 3 with a goat behind it; Berta loses.
Game 3
Candidate Conny chooses gate 1, the presenter does not open a gate, but offers the candidate 1000 Euros in exchange for not opening the gate; Conny takes the money and wins 1000 Euros.
Game 4
Candidate Doris chooses gate 1, the presenter then opens gate 3 with a goat behind it and offers Doris to reconsider her choice ...
Given the various ways the moderator can behave, Doris should carefully consider her chances of winning. If she thinks the moderator is being nice to her and wants to distract her from her first wrong choice, then she should switch. However, if she thinks the moderator is not being kind to her and just wants to distract her from her first correct choice, then she should stay with Gate 1. If Doris can't gauge the moderator - no such clues are given in the letter to the editor either - then she has no way of correctly calculating her chances of winning. In particular, once the moderator intervenes, she can no longer invoke the indifference principle, and so the answer to the question "Is there an advantage to changing your choice of gate?" in her case is "Not necessarily."
Although this already answers the letter to the editor's question, the suggestion was made to support Doris in her decision and give her a real 50:50 chance of winning. This is done by assuming that she has the option of choosing one of the two remaining goals after tossing a fair coin. In this way, she can ensure that her probability of winning is exactly 1⁄2 regardless of the moderator's intentions.
Reply from Marilyn vos Savant
Due to Marilyn vos Savant's response to the letter to the editor, the problem achieved a high level of attention internationally, even outside the professional community, and led to heated controversy. Her response was:
"Yes, you should switch. The first gate you choose has a 1⁄3 chance of winning, but the second gate has a 2⁄3 chance of winning. Here's a good way to visualize what happens. Suppose there were 1 million gates and you chose gate number 1. Then the presenter, knowing what is behind the gates and always avoiding the one gate with the prize, opens all the gates except gate number 777777. You would immediately switch to that gate, wouldn't you?"
Marilyn vos Savant does not take into account any particular motivation of the host; according to the letter to the editor, it is not impossible that the host opens a goal gate only to distract the candidate from his first, successful election. Instead, vos Savant apparently takes the letter to the editor to mean that the game show follows the same pattern over and over again:
Course of the game show: The respective candidate chooses a gate, the presenter then always opens another gate with a goat behind it and then gives the candidate another choice between the two gates that are still closed. The candidate receives the car if it is behind the gate he last chose.
Thus, it obtains as a solution the average probability of winning all possible combinations of gates chosen by each candidate, which can then be opened by the moderator. Because the first choice of a candidate is considered arbitrary and the distribution of car and goats behind the gates is considered random, each of the nine possibilities may be considered equally probable:
| Gate 1 selected | Gate 2 | Gate 3 | Moderator opens ... | Result when changing | Retention result |
| Car | Goat | Goat | Gate 2 or Gate 3 | Goat | Car |
| Goat | Car | Goat | Gate 3 | Car | Goat |
| Goat | Goat | Car | Gate 2 | Car | Goat |
| Gate 1 | Gate 2 selected | Gate 3 | |||
| Car | Goat | Goat | Gate 3 | Car | Goat |
| Goat | Car | Goat | Gate 1 or Gate 3 | Goat | Car |
| Goat | Goat | Car | Gate 1 | Car | Goat |
| Gate 1 | Gate 2 | Gate 3 selected | |||
| Car | Goat | Goat | Gate 2 | Car | Goat |
| Goat | Car | Goat | Gate 1 | Car | Goat |
| Goat | Goat | Car | Gate 1 or Gate 2 | Goat | Car |
Three out of nine candidates win by sticking with their first choice, while six out of nine candidates get the car by switching. Thus, by switching, a candidate has an average chance of winning of p = 2⁄3.
This solution can also be illustrated graphically. In the pictures of the following table the chosen gate is arbitrarily shown as the left gate:
| Behind the first selected gate is the car | Behind the first chosen gate is a goat | |
| Probability 1⁄3 | Probability 2⁄3 | |
|
|
| |
| The moderator opens one of the gates with a goat (doesn't matter which one!) | The moderator can only open the other gate with goat | |
|
|
|
|
| Switching leads to the gain of a goat | Switching leads to winning the car | |
| Switching is disadvantageous with a probability of only 1⁄3 but advantageous in 2⁄3 | ||
Strategic solution
As a result, vos Savant's conception of gameplay can also be reproduced in the following way:
The respective candidate may determine two freely chosen gates, which the moderator must open, and receives the car if it is behind one of these two gates.
Procedure taking into account the switching strategy proposed by vos Savant:
For example, if a candidate wants to have gate 2 and gate 3 opened, he would first select gate 1, which remains locked. The candidate then moves to Gate 2 when the moderator has opened Gate 3, or vice versa. The candidate thus obviously has an average chance of winning of p = 2⁄3. Accordingly, it would always be advantageous for a candidate to switch gates.
Questions and Answers
Q: What is the Monty Hall problem?
A: The Monty Hall problem is a famous probability (chance) problem based on a television game show from the United States, Let's Make a Deal. It involves three doors, one of which has a car behind it and two of which have goats behind them.
Q: What does the host know?
A: The host knows what is behind each door and always chooses to open a door with a goat behind it.
Q: Does changing choices increase the chances of getting the car?
A: Yes, changing choices increases the chances of getting the car from 1/3 (one out of three) to 2/3 (two out of three).
Q: How does this probability work?
A: In the initial door choice, there is only a 1/3 chance that the player will pick the door with the car. There is then a 2/3 chance that if they switch their choice after seeing one of the other doors opened by the host, they will get a car.
Q: Are all options equal in terms of winning or losing?
A: No, there are three different options for winning or losing depending on whether or not you change your choice after seeing one of other doors opened by the host. If you pick correctly initially and then switch your choice, you will lose; if you pick incorrectly initially but switch your choice afterwards, you will win; and if you pick correctly initially but don't switch your choice afterwards, you will also win.
Q: Is it true that switching increases your chances to win two times out of three?
A: Yes, it is true that switching increases your chances to win two times out of three.
Search within the encyclopedia