Mersenne prime

A Mersenne number is a number of the form 2^n - 1 . Specifically, $M_{n}=2^{n}-1$ denotes the th Mersenne number. The first seven Mersenne numbers $M_{n}$ are

$1,3,7,15,31,63,127$ (sequence A000225 in OEIS).

The primes among the Mersenne numbers are called Mersenne primes. The first eight Mersenne primes $M_{p}$ are

$3,7,31,127,8191,131071,524287,2147483647$ (sequence A000668 in OEIS)

for exponents $p=2,3,5,7,13,17,19,31$ (sequence A000043 in OEIS).

When represented in the dual system, Mersenne numbers show up as columns of ones, i.e. numbers that consist exclusively of ones. The nth Mersenne number in the dual system is a number with (example: $M_{3}=7=111_{2}$ ). In the binary, Mersenne numbers belong to the number palindromes, Mersenne prime numbers accordingly to the prime number palindromes.

These prime numbers take their name from the French monk and priest Marin Mersenne (1588-1648), who claimed in the preface to his Cogitata Physico-Mathematica that for $p=2,3,5,7,13,17,19,31,67,127$ and $257$ the number $M_{p}$ is a prime number.

However, he was mistaken about the numbers $M_{{67}}$ and $M_{{257}}$ overlooked the Mersenne primes $M_{{61}}$ , $M_{{89}}$ and $M_{{107}}$ . That $M_{{67}}$ is not a prime number was shown by Édouard Lucas in 1876, but it was not until 1903 that the mathematician Frank Nelson Cole was able to name the prime factors of this number. To prove that $M_{{257}}$ is not a prime number, an early calculator was used in 1932. The number $M_{{67}}$ possibly a reading error on the part of Mersenne from his correspondence with Bernard Frénicle de Bessy and Pierre de Fermat, where he p=67 confused p=61 with

Mersenne numbers also occur in the Mersenne Twister, a pseudo-random number generator.

Postmark with the 23rd Mersenne prime found at UIUC by Donald B. Gillies in 1963.

History

Mersenne numbers were first studied in antiquity in connection with perfect numbers. A natural number is called perfect if it is equal to the sum of its real divisors (example: $6=1+2+3$ ). Euclid had already shown that the number $2^{n-1}(2^{n}-1)$ is perfect if 2^n-1 a prime number ( n=2 yields the number ). 2000 years later, the inverse was shown by Euler for even perfect numbers: every even perfect number is of the form $2^{n-1}(2^{n}-1)$ where $2^{n}-1$ is a prime number.

Odd perfect numbers have not yet been found, but their existence has not yet been proven or disproven.

The first four perfect numbers $6,28,496$ and $8128$ were already known in antiquity. The search for more perfect numbers motivated the search for more Mersenne primes. The most important property to note is the following:

If a compositenumber, then $M_{n}$ also a composite number. That is divided $2^{a\cdot b}-1$ by $2^{a}-1$ and by $2^{b}-1$ without remainder can be shown by polynomial division if and are natural numbers without the zero.

It follows immediately that the exponent of a Mersenne prime $M_{p}=2^{p}-1$ is itself a prime. This property facilitates the search for Mersenne primes, since only Mersenne numbers with prime exponent need to be considered.

However, the converse conclusion that $M_{p}$ if {p} prime is false because, for example, $M_{11}'=2047=23\cdot 89$ is not a prime number.

Mersenne primes are rare: so far (December 2018), only 51 of them have been found. Since there is a particularly efficient prime test for them, the largest known primes are Mersenne primes.

Year	Event
until 1536	It is believed that for all prime numbers p, 2p-1 is prime.
1536	The German arithmetician Ulrich Rieger (Latin Hudalrichus Regius) was the first to publish the fifth perfect number ^212-(^213-1) = 4096 - 8191 = 33550336 in print in his arithmetical book Utriusque Arithmetices epitome. Since the numbers 511 and 2047 do not appear in his tabular overview, one may assume that he recognised ^211-1 = 2047 = 23 - 89 as a composite, although he does not mention this specifically.
1555	Johann Scheubel publishes in his German translation of books VII-IX of Euclid's Elements the next two perfect numbers ^216-(^217-1) = 65536 - 131071 = 8589869056 and ^218-(^219-1) = 262144 - 524287 = 137438691328. The second factors are Mersenne's primes M17 and M19. However, he did not recognise ^211-1 = 2047 = 23 - 89, as well as ^215-1 = 32767 = 7 - 31 - 151 as composite, but ^{221-1 =} 2097151 = ^{72 -} 127 - 337. (However, he does not give the decompositions at this point.) He thus erroneously obtains nine perfect numbers in his work, instead of the correct seven.
1603	Pietro Cataldi (1548-1626) shows that 2p-1 is prime for p = 17, 19 and correctly conjectures this for p = 31. Incorrectly, he also believes it for p = 23, 29 and 37.
1640	Fermat refutes Cataldi for p = 23 and p = 37: ^223-1 = 47 - 178481 and ^237-1 = 223 - 616318177 are not prime numbers.
1644	Mersenne claims that 2p-1 is prime for p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 and 257, but not prime for all other natural numbers smaller than 257 (Preface to his work Cogitata Physico-Mathematica). We now know that this assertion is false, however, because 2p-1 is prime for p = 61 (Pervushin, 1883) as well as for p = 89 (Powers, 1911) and p = 107 (Powers and Fauquembergue, 1914); moreover, ^267-1 is composite (Lucas, 1876; Cole 1903).
1738	Euler refutes Cataldi for p = 29: ^229-1 = 233 - 1103 - 2089.
1750	Euler confirms that Cataldi was right for p = 31: ^231-1 is prime.
1870	Édouard Lucas (1842-1891) formulates the theoretical basis for the Lucas-Lehmer test.
1876	Lucas confirms Mersenne: ^2127-1 is prime and contradicts: ^267-1 is not prime, factors remain unknown.
1883	Ivan Michejowitsch Pervuschin (1827-1900), a Russian mathematician and Orthodox priest from Perm/Russia, shows that ^261-1 is prime (contradiction to Mersenne).
1903	Frank Nelson Cole names the prime factors of ^267-1 = 193707721 - 761838257287.
1911	Ralph Ernest Powers contradicts Mersenne for p = 89: 2p-1 is prime.
1914	Powers also contradicts Mersenne for p = 107: 2p-1 is prime. Almost simultaneously, E. Fauquembergue also comes to this statement.
1930	Derrick Henry Lehmer (1905-1991) formulates the Lucas-Lehmer test.
1932	Lehmer shows: M(149) and M(257) are not prime, he calculates for this two hours a day on a desk calculator for a year.
1934	Powers shows: M(241) is not prime.
1944	Horace S. Uhler shows: M(157) and M(167) are not prime.
1945	Uhler shows: M(229) is not prime.
1947	Uhler shows: M(199) is not prime.
1947	The range from 1 to 257 is now completely checked. One now knows the Mersenne primes M(p) for p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107 and 127.
1951	Start of the use of computers. The length of the largest known prime number increases from 39 digits to 687 decimal places by 1952.
1963	Donald Gillies discovers M(11,213) with 3,376 digits.
1996	Joel Armengaud and George Woltman discover with GIMPS M(1,398,269) with 420,921 digits.
1999	With M(6,972,593), which has 2,098,960 digits, a prime number with more than 1 million digits is known for the first time on 1 June.
2004	On 15 May, it is proved that M(24,036,583), a number with 7,235,733 digits, is prime.
2005	On 18 February, the GIMPS project discovers the 42nd Mersenne prime: M(25,964,951) has 7,816,230 digits. Also by the GIMPS project, the 43rd Mersenne prime number is discovered on 15 December: M(30,402,457) has 9,152,052 digits.
2006	On 4 September, the GIMPS project announces the discovery of the 44th Mersenne prime number M(32,582,657) with 9,808,358 digits.
2008	On 16 September, the 45th and 46th known Mersenne prime numbers are published by the GIMPS project: M(37,156,667) (discovered on 6 September) with 11,185,272 digits and M(43,112,609) (discovered on 23 August) with 12,978,189 digits.
2009	The 47th known Mersenne prime number M(42,643,801) is discovered by the GIMPS project on 12 April and published on 12 June.
2013	The 48th known Mersenne prime number M(57,885,161) is discovered by the GIMPS project on 25 January.
2016	The 49th known Mersenne prime number M(74,207,281) is discovered by the GIMPS project on 7 January.
2017	The 50th known Mersenne prime number M(77,232,917) is discovered by the GIMPS project on 26 December.
2018	The 51st known Mersenne prime number M(82,589,933) is discovered by the GIMPS project on 7 December.

Divisibility properties of the Mersenne numbers

In the course of their long history, many results have been found about Mersenne numbers. Besides the basic divisibility property already mentioned (the number then $M_{r}$ is divisor of $M_{n}$ ), there are, for example, the following results:

If is an even number and is prime, then is a divisor of $M_{n}$ e.g. $M_{10}=1023=3\cdot 11\cdot 31,M_{12}=4095=3^{2}\cdot 5\cdot 7\cdot 13$ .

If is an odd prime number and a prime factor of Mn, then $q\equiv 1\ mod\ 2n$ and $q\equiv \pm 1\ mod\ 8$ . Example: $M_{11}=2047=23\cdot 89$ and $23=2\cdot 11+1;89=4\cdot 2\cdot 11+1$ .

If a prime number with $p\equiv 3\ mod\ 4$ , then the following equivalence holds: $2p+1$ divides the Mersenne number $M_{p}$ exactly when $2p+1$ prime. Example: is prime and leaves a remainder of when divided by . Since $23$ (as the result of $2\cdot 11+1$ ) is prime, it follows: divides the Mersenne number $M_{11}=2047$ . This statement was formulated by Leonhard Euler, but only later proved by Joseph-Louis Lagrange (see also Sophie-Germain prime).

If $M_{p}>3$ prime number, then M p + $M_{p}+2$ prime number (namely by 3 {\displaystyle ). Mersenne primes are therefore not suitable as the smaller prime of a prime twin.

If $n=2^{m}$ with then $M_{n}$ the product of the Fermat numbers to $F_{m-1}$ . Example: $M_{16}=F_{0}\cdot F_{1}\cdot F_{2}\cdot F_{3}=3\cdot 5\cdot 17\cdot 257$ .

The search for Mersenne primes

For obtaining prime records, Mersenne primes are particularly well suited in several respects, because (a) composite exponents can be disregarded because they do not generate primes, and therefore a list of candidate exponents easily be generated with prime generators, (b) from this list, as described above, the Sophie-Germain primes with $p\equiv 3\ mod\ 4$ out (such as. e.g. p = 11 → divisor 23), (c) due to the functional connection, the magnitude of the prime number grows exponentially - namely to the base two - with the argument thus one quickly obtains very large numbers, (d) with the Lucas-Lehmer test described below, a simple and effective prime number test is available.

The Lucas-Lehmer test

→ Main article: Lucas-Lehmer test

This test is a prime number test specifically tailored to Mersenne numbers, based on work done by Édouard Lucas in the 1870-1876 period and supplemented in 1930 by Derrick Henry Lehmer.

It works as follows:

be odd and prime. $S(k)$ Let the sequence be defined by $S(1)=4,S(k+1)=S(k)^{2}-2$ .

Then: $M_{p}=2^{p}-1$ is a prime number if is $M_{p}$ divisible $S(p-1)$ by

GIMPS: The Great Internet Mersenne Prime Number Search

→ Main article: Great Internet Mersenne Prime Search

As of December 2018, 51 Mersenne primes are known. With computer help, they are trying to find more Mersenne primes. Since these are very large numbers - the 51st Mersenne prime has more than 24 million digits in the decimal system - the calculations are time-consuming and organisationally complex. Calculations with such large numbers are not inherently supported by computers. You have to store the numbers in large fields and programme the basic arithmetic operations required with them. This leads to long programme runtimes.

GIMPS (Great Internet Mersenne Prime Search) therefore tries to involve as many computers as possible in the calculations. The software required for this (Prime95) was created by George Woltman and Scott Kurowski and is available for a number of computer platforms (Windows, Unix, Linux ...).

Anyone can participate, provided they have a computer with (temporarily) free CPU capacity. To do this, you have to download the software from the website and then install it. Then you register with GIMPS and ask for a number to examine. When the calculations are done (usually after several months), you report the result back to GIMPS. In the course of the computer analysis, you are also told probabilities: the probability of finding a prime number (very small, less than 1 %); the probability of finding a factor (greater). This probability is supposed to make clear the chances of success for finding a prime number.

List of all known Mersenne primes

No.	p	Number of digits of M(p)	Year	Discoverer
1	2	1	- –	- –
2	3	1	- –	- –
3	5	2	- –	- –
4	7	3	- –	- –
5	13	4	1456	- –
6	17	6	1555	Johann Scheubel
7	19	6	1555	Johann Scheubel
8	31	10	1772	Leonhard Euler
9	61	19	1883	Ivan Pervushin
10	89	27	1911	Ralph E. Powers
11	107	33	1914	Powers
12	127	39	1876	Édouard Lucas
13	521	157	1952	Raphael M. Robinson
14	607	183	1952	Robinson
15	1279	386	1952	Robinson
16	2203	664	1952	Robinson
17	2281	687	1952	Robinson
18	3217	969	1957	Hans Riesel
19	4253	1281	1961	Alexander Hurwitz
20	4423	1332	1961	Hurwitz
21	9689	2917	1963	Donald B. Gillies
22	9941	2993	1963	Gillies
23	11.213	3376	1963	Gillies
24	19.937	6002	1971	Bryant Tuckerman
25	21.701	6533	1978	Landon Curt Noll, Laura Nickel
26	23.209	6987	1979	Noll
27	44.497	13.395	1979	David Slowinski, Harry L. Nelson
28	86.243	25.962	1982	Slowinski
29	110.503	33.265	1988	Walter Colquitt, Luther Welsh Jr.
30	132.049	39.751	1983	Slowinski
31	216.091	65.050	1985	Slowinski
32	756.839	227.832	1992	Slowinski, Paul Gage
33	859.433	258.716	1994	Slowinski, Paul Gage
34	1.257.787	378.632	1996	Slowinski, Paul Gage
35	1.398.269	420.921	1996	GIMPS / Joel Armengaud
36	2.976.221	895.932	1997	GIMPS / Gordon Spence
37	3.021.377	909.526	1998	GIMPS / Roland Clarkson
38	6.972.593	2.098.960	1999	GIMPS / Nayan Hajratwala
39	13.466.917	4.053.946	2001	GIMPS / Michael Cameron
40	20.996.011	6.320.430	2003	GIMPS / Michael Shafer
41	24.036.583	7.235.733	2004	GIMPS / Josh Findley
42	25.964.951	7.816.230	2005	GIMPS / Martin Nowak
43	30.402.457	9.152.052	2005	GIMPS / Curtis Cooper, Steven Boone
44	32.582.657	9.808.358	2006	GIMPS / Curtis Cooper, Steven Boone
45	37.156.667	11.185.272	2008	GIMPS / Hans-Michael Elvenich
46	42.643.801	12.837.064	2009	GIMPS / Odd M. Strindmo
47	43.112.609	12.978.189	2008	GIMPS / Edson Smith
48?	57.885.161	17.425.170	2013	GIMPS / Curtis Cooper
49?	74.207.281	22.338.618	2016	GIMPS / Curtis Cooper
50?	77.232.917	23.249.425	2017	GIMPS / Jonathan Pace
51?	82.589.933	24.862.048	2018	GIMPS / Patrick Laroche

As of 13 March 2020, it cannot be ruled out that there are other, as yet undiscovered Mersenne primes between p = 43,112,609 and p = 82,589,933; hence the numbering from No. 48 onwards is still uncertain (and marked with a "?").

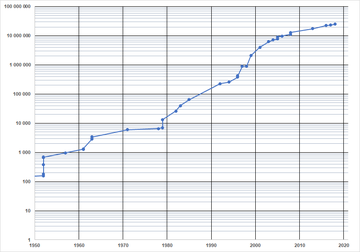
Graph of the number of digits in the largest known Mersenne primes versus year, from 1950, the most recent era of electronic calculating machines. Note: The vertical scale is a double logarithmic scale of the value of the Mersenne prime.

Open questions

As is so often the case in number theory, there are also unsolved problems concerning Mersenne numbers that are very easy to formulate:

Are there infinitely many Mersenne primes? Based on plausible heuristics, one suspects that there are $c\cdot \ln(x)$ many Mersenne primes $M_{p}$ with $p<x$ a positive constant c If this were true, there would indeed be infinitely many Mersenne primes.

More precisely, is the conjecture made by H. W. Lenstra and C. Pomerance independently made, correct, that asymptotically $e^{\gamma }\log _{2}(\log _{2}(x))+O(1)$ are many Mersenne primes less than or equal to ?
Conversely, are there infinitely many Mersenne numbers $M_{p}$ with prime that are not prime numbers? Again, one suspects the answer is yes. This would follow, for example, from the conjecture that there are infinitely many Sophie-Germain primes that are congruent 3 modulo 4.
Are all Mersenne numbers $M_{p}$ with square-free, i.e. does each prime factor occur exactly once in the prime factorisation of the number? So far, it has not even been possible to prove that this is true for infinitely many Mersenne numbers.
Does the "new Mersenne conjecture" apply? The sequence of Mersenne primes given by Mersenne suggests that he meant that a Mersenne number $M_{p}$ with } prime is prime exactly when $p=2^{k}\pm 1$ or $p=4^{k}\pm 3$ . Since this statement does not hold, P. Bateman, J. Selfridge and S. Wagstaff established the new Mersenne conjecture.

This states that from two of the following three statements the third already follows:

$n=2^{k}\pm 1$ or $n=4^{k}\pm 3$ ,
is a (Mersenne) prime number,
$(2^{n}+1)/3$ is a prime number (it is called a Wagstaff prime).

Are all members of the sequence $C(0)=2,C(k+1)=2^{C(k)}-1$ prime numbers? The stronger conjecture that all numbers $M_{M_{p}}$ are primes for which $M_{p}$ a prime was disproved by Raphael Robinson in 1957. (e.g. $M_{M_{13}}=M_{8191}$ not prime) These latter numbers are called double Mersenne numbers (OEIS, A077585). So far, double Mersenne primes are only $p=2,3,5,7$ known for (OEIS, A077586); small factors have been found for $p=13,17,19$ and Whether there are further or even infinitely many double Mersenne primes remains unknown.