Acceleration

This article describes the physical term. For the social science book, see Acceleration. The change of time structures in the modern age.

In physics, acceleration is the change in the state of motion of a body. As a physical quantity, acceleration is the instantaneous time rate of change of velocity. It is a vectorial, i.e. directed, quantity. Acceleration, along with location and velocity, is a central quantity in kinematics, a branch of mechanics.

In colloquial language, acceleration often refers only to an increase in "tempo", i.e. the amount of speed. In the physical sense, however, every change in a movement is an acceleration, e.g. also a decrease in the amount of speed - such as a braking process - or a pure change in direction with a constant amount of speed - such as when driving a car around a curve. In addition, there are terms in physics and technical mechanics such as centripetal acceleration or gravitational acceleration or similar, which are used to describe the acceleration that would occur in the movement of the body if only the force specified in the term were acting. Whether and how the body is actually accelerated, however, depends solely on the vector sum of all forces acting on it.

The SI unit of acceleration is m/s2. At an acceleration of 1 m/s2, the velocity changes by 1 m/s per second. In the geosciences, the unit Gal is also commonly used for 0.01 m/s2.

Accelerations occur in all real movement processes, e.g. of vehicles, aircraft or lifts. Due to the inertial force that occurs with them, they have a more or less significant effect on transported people and objects.

For circular movements, the angular acceleration is defined analogously as the change in angular velocity, i.e. the second time derivative of an angle.

Calculation

See also: Linear motion

The acceleration {\vec {a}} is the change in velocity per time interval. It is easiest to calculate when the acceleration is constant. If the velocities v(t_{1})at time t_{1}and v(t_{2})at time t_{2}known, the acceleration within the time interval Δ is \Delta t=t_{2}-t_{1}calculated from the difference of the velocities Δ accordance with \Delta v=v(t_{2})-v(t_{1})

a={\frac {\Delta v}{\Delta t}}.

For a constant acceleration that does not {\vec {v}}occur in the direction of the velocity vector , the difference in velocities Δ must be \Delta {\vec {v}}={\vec {v}}(t_{2})-{\vec {v}}(t_{1})determined vectorially, as illustrated in the figure. If the acceleration changes during the time period under consideration, the above calculation yields the mean acceleration, also called the average acceleration.

In order to calculate the acceleration for a specific point in time instead of for a time interval, one must go from the difference quotient to the differential quotient. The acceleration is then the first time derivative of the velocity with respect to time:

{\vec {a}}(t)={\frac {\mathrm {d} {\vec {v}}(t)}{\mathrm {d} t}}={\dot {\vec {v}}}(t)

Since velocity is the derivative of location with respect to time, acceleration can also be {\vec {r}}represented as the second derivative of the location vector

{\vec {a}}(t)={\frac {\mathrm {d} ^{2}{\vec {r}}(t)}{\mathrm {d} t^{2}}}={\ddot {\vec {r}}}(t)

The time derivative of the acceleration (i.e., the third derivative of the location vector with respect to time) is called jerk : {\vec {j}}

{\vec {j}}(t)={\dot {\vec {a}}}(t)={\frac {\mathrm {d} ^{3}{\vec {r}}(t)}{\mathrm {d} t^{3}}}

Examples of calculation via speed

A car is moving at time t_{1}=0\,\mathrm {s} with a speed of v_{1}=10\,\mathrm {\tfrac {m}{s}} across the road (which is 36 km/h). Ten seconds later, at time t_{2}=10\,\mathrm {s} , the speed is v_{2}=30\,\mathrm {\tfrac {m}{s}} (which is 108 km/h). The average acceleration of the car in this time interval was then

{\displaystyle a={\frac {v_{2}-v_{1}}{t_{2}-t_{1}}}=2\,\mathrm {\frac {m}{s^{2}}} }.

The speed has thus increased by an average of 2 m/s (i.e. by 7.2 km/h) per second.

A passenger car driving before the red light within Δ {\displaystyle \Delta t=3\,\mathrm {s} }of "speed 50" ( {\displaystyle v_{1}=50\,\mathrm {\tfrac {km}{h}} \approx 14\,\mathrm {\tfrac {m}{s}} }) is decelerated to zero, the acceleration undergoes

{\displaystyle a={\frac {0-v_{1}}{\Delta t}}\approx -5\,\mathrm {\frac {m}{s^{2}}} }.

Unit of acceleration

The standard unit of measurement for specifying an acceleration is the unit meter per square second (m/s2), i.e. (m/s)/s. In general, loads on technical equipment or the specification of load limits can be expressed as g-force, i.e. as "force per mass". This is given as a multiple of the normal acceleration due to gravity (standard acceleration due to gravity) g = 9.80665 m/s2. In the geosciences, the unit Gal = 0.01 m/s2 is also commonly used.

Acceleration of motor vehicles

For motor vehicles, the achievable positive acceleration is used as an essential parameter for classifying the performance. An average value is usually given in the form "In ... seconds from 0 to 100 km/h" (also 60, 160 or 200 km/h).

Numerical example:

For the Tesla Model S (type: Performance), it is stated that acceleration from 0 to 100 km/h can be achieved in 2.5 seconds. This corresponds to an average acceleration value of

{\displaystyle a={\frac {\Delta v}{\Delta t}}={\frac {27{,}8\,\mathrm {\frac {m}{s}} }{2{,}5\,\mathrm {s} }}=11\,\mathrm {\frac {m}{s^{2}}} }.

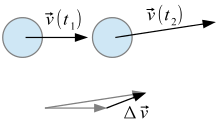
Geometric construction of the difference of velocity vectorsZoom
Geometric construction of the difference of velocity vectors

Acceleration measurement

In principle, there are two ways of measuring or specifying accelerations. The acceleration of an object can be considered kinematically with respect to a path (space curve). For this purpose, the instantaneous velocity is determined, and its rate of change is the acceleration. The other possibility is to use an accelerometer. This determines the inertial force with the aid of a test mass, from which the acceleration is then inferred with the aid of Newton's basic equation of mechanics.

Questions and Answers

Q: What is acceleration?


A: Acceleration is a measure of how fast velocity changes.

Q: How is acceleration measured?


A: Acceleration is the change of velocity divided by the change of time.

Q: What type of quantity is acceleration?


A: Acceleration is a vector, and therefore includes both a size and a direction.

Q: How is speed defined?


A: Speed is how fast you are moving, and is measured as distance traveled divided by time taken.

Q: What is the difference between speed and velocity?


A: Velocity is a vector quantity and refers to how quickly your position is changing and in what direction.

Q: What is displacement?


A: Displacement is how much your position has changed in what direction.

Q: What is jerk?


A: Jerk is the measurement of how fast acceleration changes.

AlegsaOnline.com - 2020 / 2023 - License CC3