Mandelbrot set

The Mandelbrot set, named after Benoît Mandelbrot, is the set of complex numbers for which the set of complex numbers given by the iteration

${\begin{aligned}z_{0}&=0\\z_{n+1}&=z_{n}^{2}+c\end{aligned}}$

defined sequence $(z_{n})_{n\in \mathbb {N} }$ is bounded.

Interpreted geometrically as part of the complex number plane, the Mandelbrot set is a fractal, often called the apple man in common parlance. Images of it can be generated by placing a grid of pixels on the number plane and thus assigning a value of each pixel. If the sequence is bounded by the corresponding , i.e., it belongs to the Mandelbrot set, the pixel will be colored black, for example, and white otherwise. If instead the color is determined according to how many sequence elements have to be calculated until it is determined that the sequence is not bounded, a so-called velocity image of the Mandelbrot set is created: The color of each pixel indicates how fast the sequence with the respective tends towards infinity.

The first computer graphic representations were presented by Robert Brooks and Peter Matelski in 1978. In 1980, Benoît Mandelbrot published a paper on the subject. It was later systematically studied by Adrien Douady and John Hamal Hubbard in a series of fundamental mathematical papers. The mathematical foundations for it were worked out as early as 1905 by the French mathematician Pierre Fatou.

Mandelbrot set (black) with colored environment. Each pixel is assigned a complex number Color coded is the number of necessary iterations $z_{n+1}=z_{n}^{2}+c$ , so that It increases by 1 from color stripe to color stripe. The point in the center of the image has the value 0 in the real and imaginary part of the set.

Definition

Definition via recursion

The Mandelbrot set $\mathbb {M}$ is the set of all complex numbers for which the recursively defined sequence of complex numbers $z_{0},z_{1},z_{2},\dotsc$ with the formation law

$z_{n+1}=z_{n}^{2}+c$

and the initial member

$z_{0}=0$

remains bounded. That is, a complex number is an element of the Mandelbrot set $\mathbb {M}$ if the amounts of $z_{n}$ computed with this not grow beyond any limit, no matter how large becomes. This can be written as follows:

$z_{0}=0,z_{n+1}=z_{n}^{2}+c;\;\;c\in \mathbb {M} \iff \exists g\in \mathbb {R} :\limsup _{n\to \infty }|z_{n}|\leq g$ .

One can easily show that the magnitude of $z_{n}$ grows over any limit when a $z_{n}$ with $|z_{n}|>2$ thus this definition is equivalent to:

$z_{0}=0,z_{n+1}=z_{n}^{2}+c;\;\;c\in \mathbb {M} \iff \limsup _{n\to \infty }|z_{n}|\leq 2$ .

Definition about complex quadratic polynomials

The Mandelbrot set can also be described by complex quadratic polynomials:

$P_{c}:\mathbb {C} \to \mathbb {C} ,\,z\mapsto z^{2}+c$

with a complex parameter . For each the sequence

$(P_{c}^{0}(0),\;P_{c}^{1}(0),\,P_{c}^{2}(0),\,\dotsb )=(\,P_{c}^{n}(0)\,)_{n\in \mathbb {N} }$

iteratively computed, where $P_{c}^{n}$ the -fold successive execution of the iteration, i.e.

$P_{c}^{0}(z)=z$

$P_{c}^{n+1}(z)=P_{c}(P_{c}^{n}(z)),\;n\in \mathbb {N}$ .

Depending on the value of the parameter this sequence then either grows unbounded, so that not an element of the Mandelbrot set, or it remains within a range around the origin of the number plane, and is an element of the Mandelbrot set.

The Mandelbrot set is a subset of the complex numbers with the definition

$\mathbb {M} =\lbrace c\in \mathbb {C} \;|\;\exists s\in \mathbb {R} :\forall n\in \mathbb {N} :|P_{c}^{n}(0)|\leq s\rbrace$

or equivalent

$\mathbb {M} =\lbrace c\in \mathbb {C} \;|\;\forall n\in \mathbb {N} :|P_{c}^{n}(0)|\leq 2\rbrace$ .

Some properties and examples are given for explanation:

Based on the previously described observation, can be set. Here the value gives the radius around the origin within which an element of $\mathbb {M}$ can lie. Outside this circle no elements of $\mathbb {M}$ found.
Because of the magnitude function, $\mathbb {M}$ symmetric about the real axis.
To graphically represent the set $\mathbb {M}$ graphically, the values of the parameter must all be calculated individually up to a self-determined number of iterations.
If $c=-2$ then the sequence is $0,-2,2,2,2,2,\dotsc$ and is bounded. Therefore, $c=-2$ element of $\mathbb {M}$ .
For the iterative sequence $0,2,6,38,\dotsc$ Divergence and is not an element of $\mathbb {M}$ .

Definition about Julia sets

The Mandelbrot set $\mathbb {M}$ was originally introduced by Benoît Mandelbrot to classify Julia sets, which were already studied by the French mathematicians Gaston Maurice Julia and Pierre Fatou in the early 20th century. The Julia set $J_{c}$ to a given complex number is defined as the edge of the set of all initial values $z_{0}$ , for which the above sequence of numbers remains bounded. It can be proved that the Mandelbrot set is $\mathbb {M}$ exactly the set of values for which the associated Julia set $J_{c}$ contiguous.

This principle is developed in many results on the behavior of the Mandelbrot set $\mathbb {M}$ in more depth. For example, Shishikura shows that the boundary of the Mandelbrot set $\mathbb {M}$ has Hausdorff dimension 2, as does the associated Julia set $J_{c}$ An unpublished manuscript by Jean-Christophe Yoccoz served as the basis for John Hamal Hubbard's results on locally connected Julia sets $J_{c}$ and locally connected Mandelbrot sets $\mathbb {M}$ .

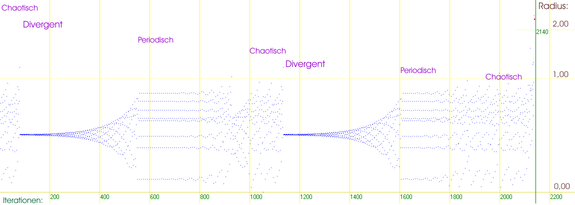
Relation to chaos theory

The law of formation, which is the basis of the sequence, is the simplest nonlinear equation, on the basis of which the transition from order to chaos can be provoked by variation of a parameter. For this purpose it is sufficient to consider real number sequences.

They are obtained when restricted to the values of the axis of $\mathbb {M}$ is constrained. For values $-0{,}75\leq c\leq 0{,}25$ , that is, inside the cardioid, the sequence converges. On the "antenna" extending to $c=-2$ the sequence behaves chaotically. The transition to chaotic behavior now occurs via an intermediate stage with periodic limit cycles. In this process, the period increases gradually toward the chaotic region by a factor of two, a phenomenon known as period doubling and bifurcation. Each to a certain period corresponds to one of the circular "buds" on the -axis.

The period doubling starts with the "head" and continues in the sequence of "buds" towards the "antenna". The ratio of the lengths of successive parameter intervals and thus that of the bud diameters to different periods thereby tends towards the Feigenbaum constant δ $\delta \approx 4{,}669$ , a fundamental constant of chaos theory. This behavior is typical of the transition of real systems to chaotic dynamics. The conspicuous gaps in the chaotic domain correspond to islands of periodic behavior, to which the satellites on the "antenna" are assigned in the complex plane.

For certain complex values, limit cycles occur which lie on a closed curve, but whose points are not covered periodically, but chaotically. Such a curve is known in chaos theory as a so-called strange attractor.

The Mandelbrot set is therefore an elementary object for chaos theory, on which fundamental phenomena can be studied. For this reason, it is sometimes compared to straight lines in Euclidean geometry in terms of its importance for chaos theory.

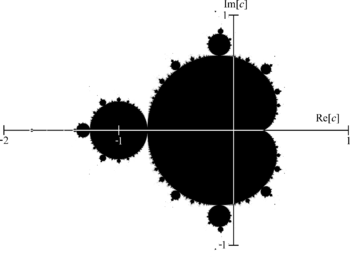
The Mandelbrot set (black) in the complex plane

The upper panel shows limit cycles of the logistic equation corresponding to real values of the Mandelbrot set. Convergence turns into chaos via bifurcation.

Behavior of the number sequence

The various structural elements of $\mathbb {M}$ closely related to certain behaviors of the sequence of numbers underlying $\mathbb {M}$ based on. Depending on the value of one of the following four possibilities results:

It converges to a fixed point.
It converges to a periodic limit cycle consisting of two or more values. This also includes the cases in which the sequence behaves periodically from the beginning.
It never repeats, but remains limited. Some values show chaotic behavior with alternation between almost periodic limit cycles and seemingly random behavior.
It diverges towards infinity (certain divergence).

All values that do not diverge determinately belong to $\mathbb {M}$ .

The following table shows examples of these four limiting behaviors of iteration $z_{n+1}=z_n^2+c$ for z_0=0 :

Parameter	Sequence members $z_{2},z_{3},z_{4},z_{5},\ldots$	Boundary behavior
On the real axis ...
$c=-3$	$6,\,33,\,1086,\,1179393,\,\dotsc$	certain divergence against $+\infty$
$c=-2$	$2,\,2,\,2,\,2,\,\dotsc$	immediate convergence to fixed point
$c=-1{,}75$	${\tfrac {21}{16}},\,-{\tfrac {7}{256}},\,-{\tfrac {114639}{65536}},\,\dotsc$	Convergence against triple limit cycle $-1{,}74697\ldots ,\,1{,}30193\ldots ,\,-0{,}54958\ldots$
$c=-1{,}5$	${\tfrac {3}{4}},\,-{\tfrac {15}{16}},\,-{\tfrac {159}{256}},\,-{\tfrac {73023}{65536}},\,\dotsc$	chaotic behavior
$c=-1{,}4$	$0{,}56,\,-1{,}0864,\,-0{,}21973504,\,\dotsc$	Convergence against 32 limit cycle
$c=-1{,}25$	${\tfrac {5}{16}},\,-{\tfrac {295}{256}},\,{\tfrac {5105}{65536}},\,\dotsc$	Convergence against alternating limit cycle $-1{,}20710\ldots ,\,0{,}20710\ldots$
$c=-1$	$-1,\,0,\,-1,\,0,\,-1,\,0,\,\dotsc$	instantaneous convergence against alternating limit cycle $-1,\,0$
$c=-0{,}75$	$-{\tfrac {3}{16}},\,-{\tfrac {183}{256}},\,-{\tfrac {15663}{65536}},\,\dotsc$	very slow convergence to fixed point $-\tfrac12$
$c=-0{,}5$	$-{\tfrac {1}{4}},\,-{\tfrac {7}{16}},\,-{\tfrac {79}{256}},\,-{\tfrac {26527}{65536}},\,\dotsc$	Convergence to fixed point ${\tfrac {1}{2}}-{\sqrt {\tfrac {3}{4}}}$
$c=-0{,}25$	$-{\tfrac {3}{16}},\,-{\tfrac {55}{256}},\,-{\tfrac {13359}{65536}},\,\dotsc$	Convergence to fixed point ${\tfrac {1}{2}}-{\sqrt {\tfrac {1}{2}}}$
$c=0$	$0,\,0,\,0,\,0,\,0,\,0,\,\dotsc$	immediate convergence to fixed point $0$
$c=+0{,}25$	${\tfrac {5}{16}},\,{\tfrac {89}{256}},\,{\tfrac {24305}{65536}},\,\dotsc$	Convergence against fixed point $\tfrac12$
$c=+1$	$2,\,5,\,26,\,677,\,458330,\,\dotsc$	certain divergence against $+\infty$
In the complex number plane ...
$c=-\mathrm {i}$	$-1-\mathrm {i} ,\,\mathrm {i} ,\,-1-\mathrm {i} ,\,\mathrm {i} ,\,\dotsc$	instantaneous convergence against alternating limit cycle $-1-\mathrm {i} ,\,\mathrm {i}$
$c=-{\tfrac {1}{8}}+{\tfrac {3}{4}}\mathrm {i}$	$-{\tfrac {43}{64}}+{\tfrac {9}{16}}\mathrm {i}$	Convergence vs. triple limit cycle

Geometric assignment

Convergence exists precisely for the values of that form the interior of the cardioids, the "body" of $\mathbb {M}$ , as well as for countably many of its boundary points. Periodic limit cycles are found in the (approximately) circular "buds" as in the "head", in the cardioids of the satellites, and also on countably many boundary points of these components. A fundamental conjecture is that there is a limit cycle for all interior points of the Mandelbrot set. The sequence is genuinely pre-periodic for countably many parameters, often called Misiurewicz-Thurston points (after Michał Misiurewicz and William Thurston). These include the "aerial peaks" such as the point $z=-2$ the far left and branching points of the Mandelbrot set.

In the uncountably many remaining points of the Mandelbrot set, the sequence can behave in many different ways, each of which generates very different dynamical systems and some of which are the subject of intensive research. Depending on the definition of the word, "chaotic" behavior can be found.

Periodic behavior

The circular structures

Each circular "bud" and each satellite cardioid is characterized by a certain periodicity of the limit cycle against which the sequence tends for the associated values. The arrangement of the "buds" on the associated cardioid follows the following rules, from which the periodicities can be read directly. Each "bud" touches exactly one base body, namely a larger "bud" or a cardioid.

The periodicity of a "bud" is the sum of the periodicities of the two nearest larger "neighboring buds" in both directions on the same basic body, if there are any. If there are only smaller "buds" at the edge of the base body up to the point of contact with its base body or up to the notch of the cardioid, then instead of the periodicity of a "neighboring bud", that of the base body itself contributes to the sum. The following properties are derived directly from this:

In tendency, the greater the periodicity of the "buds" or cardioids, the smaller they are.
The periodicity of the largest "bud" on a base body is always double, like the "chignon" with period on the "head".
The periodicity of a satellite "bud" is the product of the periodicity of the satellite cardioids and that of the corresponding "bud" of the main cardioids.

Furthermore, this rule explains the occurrence of certain sequences of "buds" such as from the "head" towards the cardioid notch with a periodicity increase towards the next "bud" by the value or from the "arm" towards the "head" by the value .

Attractive cycles

If for a there is a sequence member with the property $z_{n}=z_{0}=0$ , then the sequence repeats strictly periodically from the beginning with period . Since obtained $z_{n}$ by applying the iteration rule times, squaring at each step, it can be formulated as a polynomial of degree $2^{n-1}$ The values for periodic sequences of period are therefore obtained over the $2^{n-1}$ zeros of this polynomial are obtained. It turns out that any sequence of numbers converges to this number cycle provided one of its sequence members is sufficiently close to this cycle; these are called attractors. This leads to the fact that all number sequences converge to some neighborhood of the value, which represents the attractor, against a stable cycle of period Each circular "bud" and each cardioid of a satellite represents exactly such an environment. As an example, consider the regions with periods to :

Period 1: The cardioid of the main male apple. The edge of this cardioid is given by points of the form $c={\tfrac {1}{2}}z-{\tfrac {1}{4}}z^{2}$ with .
Period 2: The "head". The 2nd zero corresponds to the main cardioid which, because of period naturally occurs as a zero when determining all higher periods. This consideration shows that the number of attractors with period can be most 2 n $2^{n-1}-1$ , and that only if n {\displaystyle prime number. The head itself is a circular disk with center and radius ${\tfrac {1}{4}}$ , i.e., the edge of this circular disk is given by points of the form $c=-1+{\tfrac {1}{4}}z$ with .
Period 3: The "buds" corresponding to the "arms" and the cardioids of the largest satellite on the "head antenna". The fourth zero omitted again.

The number of attracting cycles with exact period , i.e. $z_{n}=z_{0}$ and is minimal with this property, is the sequence A000740 in OEIS.

Iteration gallery

The following gallery gives an overview of the values of $z_{n}$ for some values of . Here $z_{n}$ on the parameter whose real part ranges from -2.2 to +1 in the images from left to right, and whose imaginary part ranges from -1.4 to +1.4.

The iteration z → z² + c after n steps

Iterations	Description
	n = 1After the first step, $z_{1}(c)=c$ . Thus, the image is a colored representation of the complex numbers which are located in the area shown. Zero is shown in white and infinity in black. Therefore, the farther a point is from the origin, the darker it appears. The color of a point gives information about its argument, i.e. about the angle it has with the positive-real axis (red). The negative real axis is colored turquoise.
	n = 2After two steps $z_{2}(c)=c^{2}+c=c\cdot (c+1)$ This expression becomes zero for as well as for . The newly added left zero is at the center of the head of the Mandelbrot set, while the old one on the right is the heart of the Leib cycloid.
	n = 3The number of zeros has doubled - as after each iteration step. The real zero on the left is in the heart of the small antenna satellite. The first complex-valued zeros above and below the real axis appear. These zeros lie in the center of the respective little arm.
	n = 4The chignon has arisen: it belongs to the zero to the left of the head zero at -1. The represented function $z_{4}(c)=\left((c^{2}+c)^{2}+c\right)^{2}+c$ becomes more and more confusing. However, it is easy to calculate that if a zero of $z_{n}$ , is a zero of $z_{k\cdot n}$ Therefore, $z_{4}$ "inherits" the zeros of $z_{2}$ . This relationship is the cause of the periodic behavior of the buds explained below.

Iterations	Description
	n = 5Since is a prime number, there are no old known zeros - except the zero known from $z_{1}$ Since the degree of the polynomial equal to $z_{n}(c)$ $2^{n-1}$ , $z_{n}$ grows faster and faster toward infinity as grows. Thus the boundary between the Mandelbrot set and its exterior becomes clearer and clearer.
	n = 9Meanwhile there are already $256$ zeros which are also distributed within the Mandelbrot set. Since is a divisor of , the arm buds and the small antenna satellite are again in line with a zero, and therefore light up brightly.
	n = 17Another prime number.
	n = 18With $n=18$ and $2^{17}=131072$ zeros this series of images ends. could still be increased arbitrarily, which would increase the number of new buds.

From the series of images above, it can be seen for iteration level $n=18$ that the zero $c=-1$ an interior point of $\mathbb {M}$ . Thus, it depends on the number of iterations whether zeros within $\mathbb {M}$ are present or not.

Repulsive cycles

Besides attractive cycles, there are repulsive ones, which are characterized by sequences of numbers in their vicinity moving increasingly away from them. They can be achieved, however, since every $z_{n}$ apart from the situation $z_{n-1}=0$ has two potential predecessors in the sequence, differing only by their sign, because of the square in the iteration rule. values for which the associated sequence eventually enters such an unstable cycle via such a second antecedent of a period member are, for example, the "hubs" of wheel- or spiral-shaped structures as well as the endpoints of the widely used antenna-like structures, which can be formally interpreted as "hubs" of "wheels" or spirals with a single spoke. Such values are called Misiurewicz points.

A Misiurewicz point further has the property that $\mathbb {M}$ in its immediate vicinity is nearly congruent with the same section of the associated Julia set $J_{c}$ The closer to the Misiurewicz point, the better the match becomes. Since Julia sets for values inside $\mathbb {M}$ are contiguous and outside $\mathbb {M}$ Cantor sets of infinitely many islands with total area zero, they are particularly filigree in the transition zone at the edge of $\mathbb {M}$ particularly delicate. However, each Misiurewicz point is just a boundary point of $\mathbb {M}$ , and any section of the boundary of $\mathbb {M}$ , which contains points both inside $\mathbb {M}$ as well as outside of it, contains infinitely many of them. Thus the entire richness of forms of all Julia sets of this filigree type in the neighborhood of Misiurewicz points in $\mathbb {M}$ represented.

Satellites

Another structural element which accounts for the richness of forms of the Mandelbrot set are the reduced copies of itself which are found in the filigree structures of its edge. Thereby, the behavior of the number sequences within a satellite corresponds to that of the sequences in the main body in the following way. Within a satellite, all number sequences converge to limit cycles whose periods differ from those at the corresponding places in the main body of differ $\mathbb {M}$ by a factor If, for a given value from the satellite, only every -th sequence member is considered, the result is a sequence that, except for a spatial scale factor, is nearly identical to that obtained for the corresponding value in the main body of $\mathbb {M}$ . The mathematical justification for this is deep; it comes from the work of Douady and Hubbard on "polynomial mappings".

The additional structural elements in the immediate vicinity of a satellite are a consequence of the fact that between two of the considered sequence elements with the index distance there can be one with the value $z_{n}=0$ , which thus establishes a periodic course with the period However, the corresponding sequence outside the main body diverges since it has no such intermediate elements.

The Mandelbrot set itself is a universal structure which can appear in completely different nonlinear systems and classification rules. However, the basic prerequisite is that the functions involved are angle-faithful. If such systems are considered which depend on a complex parameter and classify their behavior with respect to a certain property of the dynamics depending on , then small copies of the Mandelbrot set are found in the parameter level under certain circumstances. An example is the question for which third-degree polynomials Newton's iterative method for determining zeros with a certain initial value fails and for which it does not.

As in the adjacent picture, the Mandelbrot set can appear distorted, for example, the arm buds are located in a slightly different place. Otherwise, however, the Mandelbrot set is completely intact, including all buds, satellites, filaments and antennae. The reason for the appearance of the Mandelbrot set is that the considered function families in certain areas - apart from rotations and displacements - agree quite well with the function family

$\{f_{c}\colon z\mapsto z^{2}+c\mid c\in \mathbb {C} \}$ ,

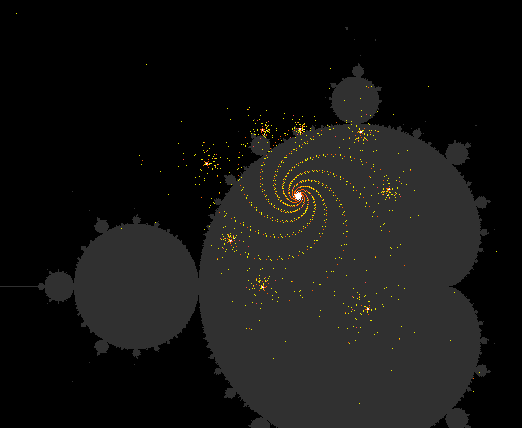
which defines the Mandelbrot set, coincide. Deviations are allowed within a certain range, and nevertheless the Mandelbrot set crystallizes. This phenomenon is called structural stability and is, in effect, responsible for the appearance of the satellites in the neighborhood of $\mathbb {M}$ , because subsequences of the iterated functions locally exhibit the same behavior as the total family.

Intermediate changeable behavior

Due to the possibility of the sequence of numbers to repeatedly get into the immediate vicinity of a repulsive cycle, and in turn to almost get into another cycle during the subsequent tending divergent or chaotic behavior, intermediately very complicated behaviors of the sequence can be formed until the final character of the sequence is revealed, as the two figures demonstrate. The environment of the associated values in $\mathbb {M}$ is correspondingly rich in structure.

The representation of the following points even in the complex plane shows greater complexity in these cases. The quasiperiodic behavior in the neighborhood of a repulsive cycle in these cases often leads to spiral structures with several arms, where the following points orbit the center while the distance to it increases. The number of arms is therefore equal to the period. The point clusters at the ends of the spiral arms in the figure above are the result of the two associated near-captures by repulsive (unstable) cycles.

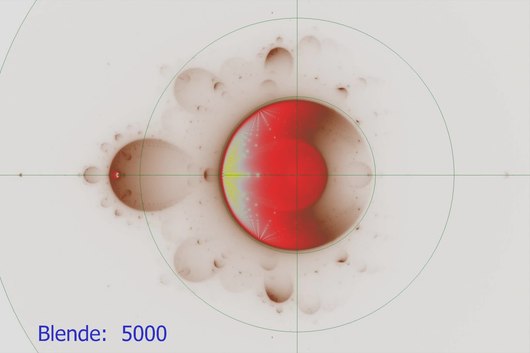
Density distribution of the sequence members

The adjacent picture shows how often a pixel is hit by an intermediate result of all iterations. In the range of |Z|<2.0 each pixel is hit at least once and added up. Within M, values up to 30000 can occur in this image. However, at a contrast of 1:30000, subtleties in the M edge can no longer be easily seen. At apertures up to 1000, structures can be seen that lie far outside the M. These are generated by the intermediate results of the periodic iterations of satellite sets.

In the orbit image all iteration results were filtered out which are not contained in the selection range at point 1. So you can see that these orbits start from a satellite of period 3 (point S). In the next pictures these 4 orbit summations are shown zoomed. This example is valid for all satellites. However, for most satellites a much higher iteration limit is needed (here only 100). This increases the generated contrast considerably, making such subtleties increasingly difficult to show.

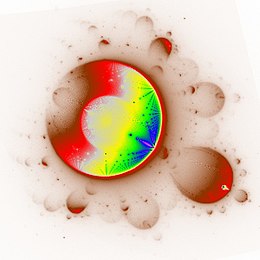
Figure 3 of the orbit

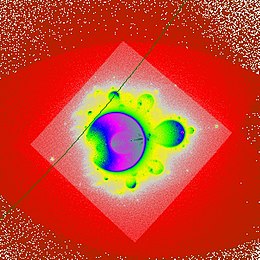
Figure 2 of the orbit

Figure 1 of the orbit

Orbit origin in satellite (S)

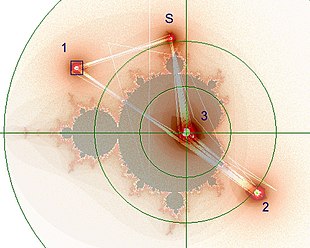
Orbit image

Play media file

Accumulated density distribution of the sequence members for all values in a color-coded plot.

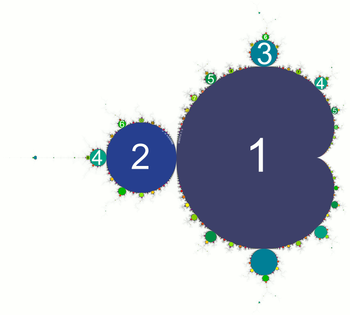
Mandelbrot set with color-coded period length of limit cycles

Analysis of the behavior of Newton's method to a family of cubic polynomials.

Representation of the amount of the sequence members as a function of the iteration step for a value with particularly varied behavior of the sequence. The conspicuous breaks in the behavior result from near catches in repulsive cycles, which temporarily leads to quasiperiodic behavior.

Display the sequence members to the value of the previous graph as points in the complex plane with a background Mandelbrot set for orientation. The brightness of a pixel is a measure of how many points of the sequence it was hit by.