Magnetic reluctance

The magnetic resistance or reluctance $R_{\text{m}}$ is the proportionality factor between the magnetic voltage $U_{\text{m}}$ and the magnetic flux $\Phi$ in the form:

$U_{\text{m}}=R_{\text{m}}\cdot \Phi$

The equation is called Hopkinson's law or Hopkin's law after John Hopkinson and has a similar form to Ohm's law for the electric circuit if the magnetic flux $\Phi$ analogous to the electric current and the magnetic voltage $U_{\text{m}}$ analogous to the electric voltage . The magnetic resistance is not to be confused with the magnetoresistive effect, which describes an electrical resistance that is influenced by a magnetic flux.

Due to the historically conditioned term formation, the magnetic voltage $U_{\text{m}}$ sometimes also referred to in the $\Theta$ technical literature as magnetic flux with the formula symbol

The magnetic resistance for an element with uniform magnetic flux corresponds to the size:

$R_{\text{m}}={\frac {l}{\mu _{0}\cdot \mu _{\text{r}}\cdot A}}$

Thereby corresponds

the length of the magnetic circle in metres,

$\mu _{0}$ the permeability of vacuum ( $4\pi \cdot 10^{-7}$ Henry per metre),

$\mu _{\text{r}}$ the relative permeability of the material (dimensionless),

the cross-sectional area of the magnetic conductor in square metres.

For magnetic circuits with sectionally constant magnetic conductance values, cross-sections and lengths, magnetic partial resistances can be determined according to the above relationship. The calculation rules for combining these resistors are analogous to those for the series and parallel connection of electrical resistors.

The total resistance in the magnetic circuit is also decisive for its inductance and magnetic flux density .

Magnetic resistors are used in the theory of magnetic circuits developed by John Hopkinson and his son Edward Hopkinson at the end of the 19th century. The ideas developed at that time were a basis for the construction of electrical machines and are still used today to understand simple magnetic circuits.

The reciprocal of the magnetic resistance is the magnetic conductance or permeance $G_{\text{m}}$ .

The unit of magnetic resistance $R_{\text{m}}$ in the International System of Units (SI) is the reciprocal of the unit Henry and can be expressed as H-1. The unit of magnetic conductance $G_{\text{m}}$ is the Henry.

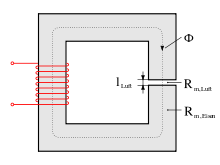
Iron core with air gap Rm = Rm,iron + Rm,air

Questions and Answers

Q: What is magnetic reluctance?

A: Magnetic reluctance is a measurement used in the analysis of magnetic circuits, similar to resistance in an electrical circuit.

Q: What does magnetic reluctance do?

A: It stores magnetic energy instead of dissipating it.

Q: How does a magnetic field affect magnetic flux?

A: A magnetic field causes magnetic flux to follow the path of least magnetic reluctance.

Q: Is reluctance a scalar or a vector quantity?

A: Reluctance is a scalar quantity.

Q: Is reluctance an extensive or intensive quantity?

A: Reluctance is an extensive quantity.

Q: How is reluctance typically represented?

A: Reluctance is usually represented by the symbol ℜ.

Q: What is the relationship between magnetic and electrical resistance?

A: While magnetic reluctance is similar to electrical resistance, it pertains to the storage and flow of magnetic energy, whereas electrical resistance pertains to the storage and flow of electrical energy.