Magnetic moment

In physics, the magnetic dipole moment (or magnetic moment) $\vec{m}$ is a measure of the strength of a magnetic dipole and is defined analogously to the electric dipole moment.

A magnetic dipole in an external magnetic field of flux density ${\vec {B}}$ acted upon by a torque

${\vec D}_{{{\vec m}}}={\vec m}\times {\vec B}\,,$

by which it is rotated in the field direction ( $\times$ : cross product). Its potential energy therefore depends on the setting angle θ $\theta$ between field direction and magnetic moment:

$E_{{{\text{pot}}}}=-{\vec m}\cdot {\vec B}\equiv -m\,B\cos \theta .$

Important examples are the compass needle and the electric motor.

The unit of measurement of the magnetic moment in the International System of Units (SI) is A-m2. Often the product of $\vec{m}$ and the magnetic field constant μ $\mu _{0}$ used; this has the SI unit T-m3.

Equality within a set or structure

A magnetic moment can be the result of an electric current:

The current density distribution ${\vec {\jmath }}\,({\vec r})$ has a magnetic moment

${\vec {m}}={\frac {1}{2}}\int \limits _{\mathbb {R} ^{3}}\mathrm {d} ^{3}r\left[{\vec {r}}\times {\vec {\jmath }}\,({\vec {r}})\right].$

For a plane current loop this results in

$m=I\cdot A$

where the area flowed around by the current

In electrical engineering, this is the basis for generators, motors and electromagnets, for example.

Particles with intrinsic angular momentum (spin) ${\vec {s}}$ have magnetic momentum

${\vec {m}}=\gamma {\vec {s}}.$

$\gamma$ is called gyromagnetic ratio. Examples include electrons, which give rise to the ferromagnetism of iron group elements and rare earth elements due to the parallel position of their magnetic moments. Ferromagnetic materials are used as permanent magnets or as iron cores in electromagnets and transformers.

Examples

Plane conductor loop

The following applies to a closed conductor loop

$\int {\vec {\jmath }}\,({\vec {r}})\;{\mathrm {d}}^{3}r=\int I\;{\mathrm {d}}{\vec {r}}.$

Thereby denotes

${\vec {\jmath }}\,({\vec {r}})$ the current density at location ${\vec {r}}$
$\int {\mathrm {d}}^{3}r$ a volume integral
the current through the conductor loop
$\int {\mathrm {d}}{\vec {r}}$ a path integral along the conductor loop.

Thus it follows for the magnetic dipole moment:

${\vec {m}}={\frac {I}{2}}\int _{C}({\vec {r}}\times {\mathrm {d}}{\vec {r}})=I\cdot {\vec {A}}=I\cdot A\cdot {\vec {n}}_{A}$

with the normal vector ${\vec {n}}_{A}$ on the plane surface . The vector ${\vec {n}}_{A}$ is oriented so that it points upward when the current is flowing counterclockwise.

Current carrying long coil

The magnetic moment of a current-carrying coil is the product of the number of turns , current and area :

${\vec {m}}=n\cdot I\cdot {\vec {A}}.$

Where ${\vec {A}}={\vec {n}}_{A}A$ the vector belonging tothe surface

Charged particle on a circular path

Classic

If the circular current is caused by a particle with mass and charge orbiting on a circular path (radius , orbital period ), this formula yields

${\vec {m}}=IA\;{\vec {n}}_{A}={\frac {Q}{T}}\cdot \pi r^{2}\;{\vec {n}}_{A}\equiv {\frac {Q}{2M}}{\vec L}\quad .$

The magnetic moment is thus fixed with the angular momentum

${\vec {L}}=\omega Mr^{2}\;{\vec {n}}_{A}$

linked. The constant factor γ $\gamma ={\tfrac {Q}{2M}}$ is the gyromagnetic ratio for moving charge on the circular path. (In the conversion, the angular velocity ω $\omega ={\tfrac {2\pi }{T}}$ used).

Quantum mechanical

The classical formula plays a major role in atomic and nuclear physics, because it is also valid in quantum mechanics, and a well-determined angular momentum belongs to each energy level of a single atom or nucleus. Since the angular momentum of spatial motion (orbital angular momentum, unlike spin) can only be integer multiples of the constant $\hbar$ (Planck's constant), the magnetic orbital momentum also has a smallest "unit" called a magneton:

$\mu ={\frac {Q\hbar }{2M}}\quad .$

If the elementary charge substituted for , the Bohr magneton μ $\mu _{\mathrm {B} }={\tfrac {e\hbar }{2m_{\mathrm {e} }}}$ , for the proton the nuclear magneton μ $\mu _{\mathrm {K} }={\tfrac {e\hbar }{2m_{\mathrm {p} }}}$ . Since the proton mass $m_{\mathrm {p} }$ is nearly 2000 times larger than the electron mass $m_{{\mathrm e}}$ , the nuclear magneton is smaller than the Bohr magneton by the same factor.

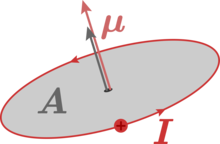
Magnetic dipole moment of a surface with current flowing around it

The magnetic moment of particles and nuclei

Particles and atomic nuclei with a spin ${\vec {s}}$ have a magnetic spin moment μ ${\vec {\mu }}_{s}$ , which is parallel (or antiparallel) to their spin, but has a different magnitude relative to spin than if it came from an orbital angular momentum of the same magnitude. This is expressed by the anomalous Landé factor of spin $g_{s}{\mathord {\neq }}1$ One writes for electron ( $\mathrm {e} ^{-}$ ) and positron ( $\mathrm {e} ^{+}$ )

${\vec {\mu }}_{s}=g_{e}\,\mu _{\mathrm {B} }\,{\frac {\vec {s}}{\hbar }}$ with the Bohr magneton μ \mu $\mu _{\mathrm {B} }$ ,

for proton (p) and neutron (n)

${\vec {\mu }}_{s}=g_{p,n}\,\mu _{\mathrm {K} }\,{\frac {\vec {s}}{\hbar }}$ with the nuclear magneton μ $\mu _{\mathrm {K} }$ ,

and correspondingly for other particles. The dipole moments of the atomic nuclei and their effects like the hyperfine structure are very weak and difficult to observe compared to the fine structure splitting based on electron dipole moments.

For the muon, instead of the mass of the electron, that of the muon is used in the magneton, and for the quarks, their respective constituent mass and third-integer electric charge.

If the magnetic moment is antiparallel to the spin, the g-factor is negative. However, this sign convention is not universally applied, so that often the g-factor of e.g. the electron is given as positive.

Particle	Spin-g factor
Electron $e^{-}$	$-2{,}002\,319\,304\,362\,56(35)$
Muon μ $\mu ^{-}$	$-2{,}002\,331\,8418(13)$
Proton	$+5{,}585\,694\,6893(16)$
Neutron	$-3{,}826\,085\,45(90)$

The bracketed numbers indicate the estimated standard deviation.

According to Dirac theory, the Landé factor of fundamental fermions is exactly $g_{s}{\mathord =}\pm 2$ , quantum electrodynamics $g_{s}{\mathord =}\pm 2{,}0023$ predicts a value of about Precise measurements on the electron and positron, respectively, and on the muon are in excellent agreement with this, including the predicted small difference between the electron and muon, thus confirming Dirac theory and quantum electrodynamics. The strongly deviating g-factors for the nucleons can be explained, albeit with deviations in the percentage range, by their construction from three constituent quarks each.

If the particles (e.g., electrons bound to an atomic nucleus) additionally exhibit orbital angular momentum, the magnetic moment is the sum of μ ${\vec {\mu }}_{s}$ , the magnetic moment of the spin considered above, and μ ${\vec {\mu }}_{\ell }$ , that of the orbital angular momentum:

${\vec {\mu }}={\vec {\mu }}_{s}+{\vec {\mu }}_{\ell }$ .

Magnetic field of a magnetic dipole

A magnetic dipole $\vec{m}$ at the coordinate origin leads to a magnetic flux density at location ${\vec {r}}$

${\vec {B}}({\vec {r}})\,=\,{\frac {\mu _{0}}{4\pi }}\,{\frac {3{\vec {r}}({\vec {m}}\cdot {\vec {r}})-{\vec {m}}r^{2}}{r^{5}}}$ .

In it μ $\mu _{0}$ the magnetic field constant. Except at the origin, where the field diverges, both the rotation and the divergence of this field vanish everywhere. The corresponding vector potential is given by

${\vec {A}}({\vec {r}})\,=\,{\frac {\mu _{0}}{4\pi }}\,{\frac {{\vec {m}}\times {\vec {r}}}{r^{3}}}$ ,

where ${\vec {B}}=\nabla \times {\vec {A}}$ . With magnetic field strength the magnetic scalar potential is ${\vec {H}}=-\nabla \psi$

$\psi ({\vec {r}})\,=\,{\frac {1}{4\pi }}\,{\frac {{\vec {m}}\cdot {\vec {r}}}{r^{3}}}$ .

Force and moment action between magnetic dipoles.

Force effect between two dipoles

The force exerted by dipole 1 on dipole 2 is

${\vec {F}}=\nabla \left({\vec {m}}_{2}\cdot {\vec {B}}_{1}\right)$

It results

${\mathbf {F}}({\vec {r}},{\vec {m}}_{1},{\vec {m}}_{2})={\frac {3\mu _{0}}{4\pi r^{4}}}\left[{\vec {m}}_{2}({\vec {m}}_{1}\cdot {\vec {r}}_{n})+{\vec {m}}_{1}({\vec {m}}_{2}\cdot {\vec {r}}_{n})+{\vec {r}}_{n}({\vec {m}}_{1}\cdot {\vec {m}}_{2})-5{\vec {r}}_{n}({\vec {m}}_{1}\cdot {\vec {r}}_{n})({\vec {m}}_{2}\cdot {\vec {r}}_{n})\right],$

where ${\vec {r}}_{n}$ is the unit vector pointing from dipole 1 to dipole 2 and is the distance between the two magnets. The force on dipole 1 is reciprocal.

Torque effect between two dipoles

The torque exerted by dipole 1 on dipole 2 is

${\vec {M}}={\vec {m}}_{2}\times {\vec {B}}_{1}$

where ${\vec {B}}_{1}$ is the field generated by dipole 1 at the location of dipole 2 (see above). The torque on dipole 1 is reciprocal.

In the presence of multiple dipoles, the forces or moments can be superimposed. Since soft magnetic materials form a field-dependent dipole, these equations are not applicable.

Questions and Answers

Q: What is the magnetic moment of a magnet?

A: The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it.

Q: Which objects have magnetic moments?

A: A loop of electric current, a bar magnet, an electron, a molecule, and a planet all have magnetic moments.

Q: How can both the magnetic moment and magnetic field be considered?

A: Both the magnetic moment and magnetic field may be considered to be vectors having a magnitude and direction.

Q: Which direction does the magnetic moment point in a magnet?

A: The direction of the magnetic moment points from the south to north pole of a magnet.

Q: What is the relationship between the magnetic moment and magnetic field of a magnet?

A: The magnetic field produced by a magnet is proportional to its magnetic moment.

Q: What does the term magnetic moment normally refer to?

A: More precisely, the term magnetic moment normally refers to a system's magnetic dipole moment, which produces the first term in the multipole expansion of a general magnetic field.

Q: How does the dipole component of an object's magnetic field behave as distance from the object increases?

A: The dipole component of an object's magnetic field is symmetric about the direction of its magnetic dipole moment, and decreases as the inverse cube of the distance from the object.