Lorenz system
The Lorenz attractor is the strange attractor of a system of three coupled nonlinear ordinary differential equations:
The system was formulated around 1963 by the meteorologist Edward N. Lorenz (1917-2008), who developed it as an idealization of a hydrodynamic system. Based on a work by Barry Saltzman (1931-2001), Lorenz was concerned with modelling the conditions in the Earth's atmosphere for the purpose of long-term forecasting. However, Lorenz emphasized that the system he developed provides 
Closely connected with the Lorenz attractor is the catchword of the butterfly effect (metaphor from chaos research). The system of differential equations was repeatedly in the public eye, which tried to explain real-world phenomena with the chaotic behavior of mathematical equations: Thus, the Lorenz system was supposed to illustrate that in the atmospheric flow pattern, small causes can have a large effect.
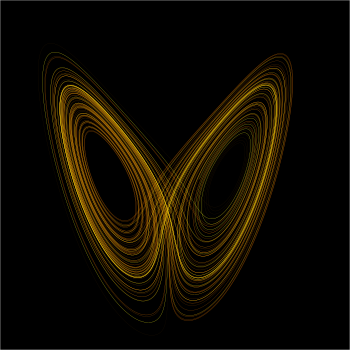
Graphical representation of a Lorenz-Attractor

Animated Lorenz attractor; click to start animation
Derivation
To derive the Lorenz equation as a description of convection currents, the following model was considered, which was investigated experimentally by the French physicist Henri Bénard at the turn of the century and described theoretically by the British Nobel Prize winner Lord Rayleigh in 1916:
A viscous incompressible fluid (liquid) is located between two plates with a small distance. While small temperature differences between the top and bottom of the layer can still be compensated for by heat conduction, when a critical temperature difference is exceeded, fluid movement sets in and convection rolls are formed, through which more efficient heat transport is realized. In this process, fluid elements heated from below rise due to their lower density and colder fluid volumes sink.
The mathematical description of the model by the Navier-Stokes equations leads via various simplifications, for example finitely broken row representations, to the system of equations given above.
Hermann Haken showed that the Lorenz system can also be used to model processes in lasers, since the system is equivalent to the Maxwell-Bloch equations.
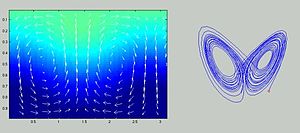
Convection model, assigned point in phase space.
Chaos Theory
The numerical solution of the system shows deterministically chaotic behavior for certain parameter values, the trajectories follow a strange attractor. Thus the Lorenz attractor plays a role for mathematical chaos theory, because the equations represent probably one of the simplest systems with chaotic behavior.
The typical parameter setting with chaotic solution is: 



After the clarification of the physical-technical basics by the physicists and meteorologists mentioned above, numerous well-known mathematicians dealt with the problem in the second half of the 20th century, among them the American mathematician John Guckenheimer. The proof that the Lorenzattractor is a so-called strange attractor was provided only in 1999 by the mathematician Warwick Tucker.
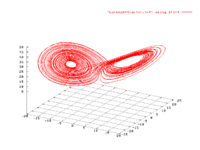
Butterfly graph: A 3D representation of 2900 points of the Lorenz attractor computed numerically using a fixed step size Runge-Kutta method.
Search within the encyclopedia
