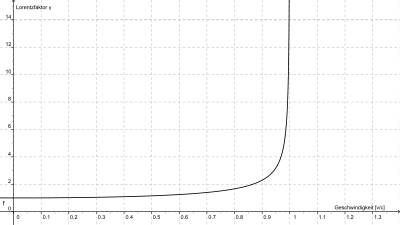
Lorentz factor

The dimensionless Lorentz factor γ $\gamma$ (gamma) describes in special relativity the time dilation as well as the reciprocal of the length contraction in the coordinate transformation between inertial systems moving relative to each other. It was developed by Hendrik Antoon Lorentz within the framework of the Lorentz transformation he devised, which forms the mathematical basis of special relativity.

The Lorentz factor is defined as:

$\gamma ={\frac {1}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}\geq 1$

denotes the relative velocity of two reference systems.
The speed of light is a natural constant independent of the reference frame.

The following applies to reference systems at rest relative to each other

$v=0\Rightarrow \gamma =1.$

If $v\neq 0$ but still small compared to the speed of light

$v \ll c \Leftrightarrow \frac{v}{c} \ll 1,$

Thus, through a Taylor development

$\gamma =1+{\frac {1}{2}}{\frac {v^{2}}{c^{2}}}+{\frac {3}{8}}{\frac {v^{4}}{c^{4}}}+{\mathcal {O}}\left({\frac {v^{6}}{c^{6}}}\right)$

At which order the evolution can be terminated in classical physics cannot be answered in general. For most applications, γ $\gamma$ can be assumed to be constant one, for the kinetic energy the first order proportional to $v^{2}$ decisive.

Lorentz factor γ $\gamma$ as a function of in units of i.e. as a function of ${\tfrac {v}{c}}$

Lorentz factor for accelerations

The time derivative of γ $\gamma$ is interesting to formulate the relativistic form of Newton's second law $\vec F = m \vec a$ for accelerations in the direction of motion, since the relativistically correct relation is ${\vec {F}}={\tfrac {\mathrm {d} }{\mathrm {d} t}}{\vec {p}}$ over momentum. It holds: ${\vec p}=\gamma m{\vec v}$ .

It follows directly:

${\vec {F}}=\left({\frac {\mathrm {d} }{\mathrm {d} t}}\gamma \right)m{\vec {v}}+\gamma m{\frac {\mathrm {d} }{\mathrm {d} t}}{\vec {v}}+\gamma {\vec {v}}{\frac {\mathrm {d} }{\mathrm {d} t}}m$

and one obtains for the time derivative of the Lorentz factor:

${\frac {\mathrm {d} }{\mathrm {d} t}}\gamma =\gamma ^{3}{\frac {\vec {v}}{c}}\cdot {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\vec {v}}{c}}$

and thus for the correct relationship between force and acceleration:

${\vec {F}}=m\gamma ^{3}\left({\frac {\vec {v}}{c}}\cdot {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\vec {v}}{c}}\right){\vec {v}}+\gamma m{\frac {\mathrm {d} }{\mathrm {d} t}}{\vec {v}}+\gamma {\vec {v}}{\frac {\mathrm {d} }{\mathrm {d} t}}m.$

Lorentz factor as a function of momentum p

The Lorentz factor can also be expressed as:

$\gamma ={\sqrt {1+\left({\frac {\vec {p}}{mc}}\right)^{2}}}$

with

the relativistic momentum ${\vec {p}}$ of the object under consideration
its mass

This notation is mainly found in theoretical physics.

The equivalence can be proven by an equation with the "normal" Lorentz factor, which yields the relativistic momentum.

${\vec {p}}^{2}=\underbrace {(\gamma ^{2}-1)c^{2}} _{\left({\frac {1}{1-\beta ^{2}}}-{\frac {1-\beta ^{2}}{1-\beta ^{2}}}\right)c^{2}=\beta ^{2}c^{2}\gamma ^{2}}m^{2}=\gamma ^{2}v^{2}m^{2}$

Lorentz factor as a function of kinetic energy

The Lorentz factor can also be expressed as:

$\gamma ={\frac {E_{\mathrm {kin} }}{E_{0}}}+1$

with

the kinetic energy $E_{\mathrm {kin} }$ of the considered object
of its rest energy $E_{0}.$

Questions and Answers

Q: What is the Lorentz factor?

A: The Lorentz factor is a factor by which time, length, and mass change for an object moving at relativistic speeds (close to the speed of light).

Q: Who is it named after?

A: The Lorentz factor is named after Dutch physicist Hendrik Lorentz.

Q: What equation describes the Lorentz factor?

A: The equation for the Lorentz factor is gamma = 1/(sqrt(1-(v/c)^2)), where v is the speed of the object and c is the speed of light.

Q: What does (v/c) represent in this equation?

A: In this equation, (v/c) represents beta (beta), or the ratio between an object's velocity and that of light.

Q: How can we rewrite this equation?

A: We can rewrite this equation as gamma = 1/(sqrt(1-beta^2)).