Linear map

A linear mapping (also called linear transformation or vector space homomorphism) is an important type of mapping between two vector spaces over the same body in linear algebra. In a linear mapping, it is irrelevant whether one first adds two vectors and then maps their sum, or first maps the vectors and then forms the sum of the images. The same applies to the multiplication with a scalar from the basic body.

The illustrated example of a reflection on the Y-axis illustrates this. The vector is the sum of the vectors and and its image is the vector {c'} . {c'} However, also obtained by adding the images {a'} and {b'} of the vectors and

It is then said that a linear mapping is compatible with the links vector addition and scalar multiplication. Thus, the linear mapping is a homomorphism (structure-preserving mapping) between vector spaces.

In functional analysis, when considering infinite-dimensional vector spaces carrying a topology, one usually speaks of linear operators instead of linear mappings. Formally, the terms are synonymous. However, for infinite-dimensional vector spaces the question of continuity is significant, while continuity always exists for linear mappings between finite-dimensional real vector spaces (each with the Euclidean norm) or, more generally, between finite-dimensional Hausdorff topological vector spaces.

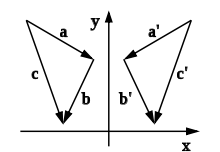
Axis mirroring as an example of a linear mapping

Definition

Let and be vector spaces over a common ground body . A mapping $f\colon V \to W$ is called a linear mapping if for all $x,y \in V$ and $a \in K$ the following conditions hold:

is homogeneous:

$f\left(a x\right) = a f\left(x\right)$

is additive:

$f\left(x+y\right)=f\left(x\right)+f\left(y\right)$

The two conditions above can also be combined:

$f\left(ax + y\right) = af\left(x\right) + f\left(y\right)$

For y = 0_V this transitions into the condition for homogeneity and for a = 1_K into that for additivity. Another equivalent condition is the requirement that the graph of the mapping is a subvector space of the sum of the vector spaces and

Explanation

A mapping is linear if it is compatible with the vector space structure. That is, linear mappings are compatible with both the underlying addition and scalar multiplication of the domain of definitions and values. Compatibility with addition means that the linear mapping $f\colon V\to W$ preserves sums. If we $v_{1},v_{2},v_{3}\in V$ have a sum $v_{3}=v_{1}+v_{2}$ with the domain of definition, then $f(v_{3})=f(v_{1})+f(v_{2})$ and thus this sum is preserved after the mapping in the range of values:

$\forall v_{1},v_{2},v_{3}\in V{\Big (}v_{3}=v_{1}+v_{2}\implies f(v_{3})=f(v_{1})+f(v_{2}){\Big )}$

This implication can be shortened by $f(v_{3})=f(v_{1})+f(v_{2})$ substituting the premise $v_{3}=v_{1}+v_{2}$ into Thus, we obtain the requirement $f(v_{1}+v_{2})=f(v_{1})+f(v_{2})$ . Analogously, compatibility can be described by scalar multiplication. This is satisfied if from the relation ${\tilde {v}}=\lambda v$ with the scalar λ $\lambda \in K$ and $v\in V$ in the domain of definition it follows that also $f({\tilde {v}})=\lambda f(v)$ holds in the domain of values:

$\forall {\tilde {v}},v\in V\,\forall \lambda \in K{\Big (}{\tilde {v}}=\lambda v\implies f({\tilde {v}})=\lambda f(v){\Big )}$

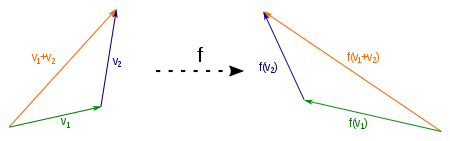
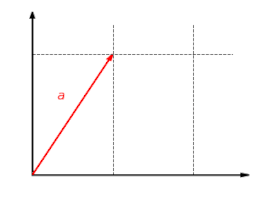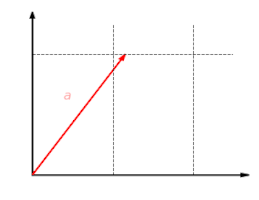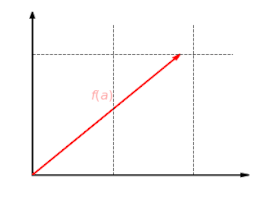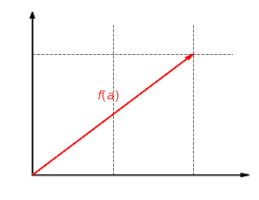
After substituting the premise ${\tilde {v}}=\lambda v$ into the conclusion $f({\tilde {v}})=\lambda f(v)$ we obtain the claim $f(\lambda v)=\lambda f(v)$ .

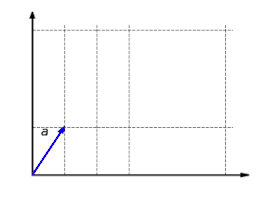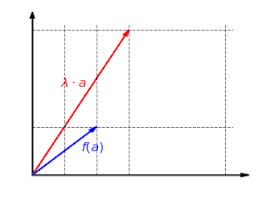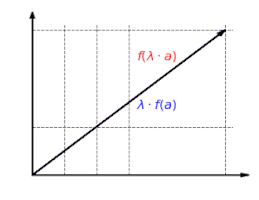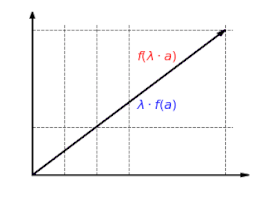
Visualization of compatibility with vector addition: each vector given by $v_{1}$ , $v_{2}$ and $v_{3}=v_{1}+v_{2}$ addition triangle is preserved by the linear mapping Also $f(v_{1})$ , $f(v_{2})$ and $f(v_{1}+v_{2})$ forms an addition triangle and it holds that $f(v_{1}+v_{2})=f(v_{1})+f(v_{2})$ .

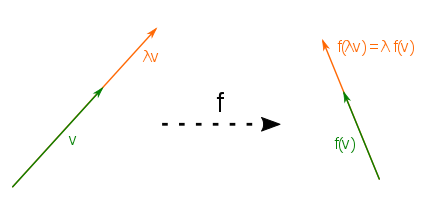
For mappings that are not compatible with addition, there are vectors $v_{1}$ , $v_{2}$ and $v_{3}=v_{1}+v_{2}$ , so that $f(v_{1})$ , $f(v_{2})$ and $f(v_{1}+v_{2})$ not form an addition triangle because $f(v_{1}+v_{2})\neq f(v_{1})+f(v_{2})$ . Such a mapping is not linear.

Visualization of compatibility with scalar multiplication: any scaling λ $\lambda v$ preserved by a linear mapping and it holds $f(\lambda v)=\lambda f(v)$ .

If a mapping is not compatible with scalar multiplication, then there is a scalar λ $\lambda$ and a vector , such that the scaling λ $\lambda v$ not $\lambda f(v)$ map to the scaling λ Such a mapping is not linear.

Examples

For any linear mapping has the form $V = W = \R$ with $m \in \R$ .
Let $V=\mathbb {R} ^{n}$ and $W = \R^m$ . Then, for each $m\times n$ -matrix using matrix multiplication, we obtain a linear mapping
$f \colon \R^n \to \R^m$
by

defined. Any linear mapping from $f(x)=A\,x={\begin{pmatrix}a_{{11}}&\dots &a_{{1n}}\\\vdots &&\vdots \\a_{{m1}}&\dots &a_{{mn}}\end{pmatrix}}{\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}$ $\mathbb {R} ^{n}$ to $\mathbb {R} ^{m}$ can be represented in this way.
If $I\subset \mathbb {R}$ an open interval, $V = C^1(I,\R)$ the $\mathbb {R}$ -vector space of continuously differentiable functions on and $W = C^0(I,\R)$ of $\mathbb {R}$ -vector space of continuous functions on , then the mapping
$D \colon C^1(I,\R) \to C^0(I,\R)$ , $f \mapsto f'$ ,
which assigns to
each function $f \in C^1(I,\R)$ its derivative, linear. The same holds for other linear differential operators.

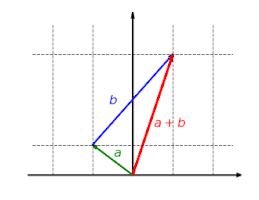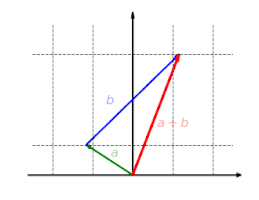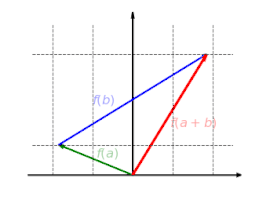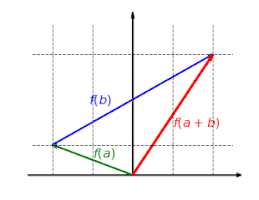
The stretch $f(x,y)=(2x,y)$ is a linear mapping. In this mapping, the component is stretched by a factor of .

This mapping is additive: it doesn't matter if you first add vectors and then map them, or if you first map the vectors and then add them: f(a+b)=f(a)+f(b) .

This mapping is homogeneous: it does not matter whether you first scale a vector and then map it, or whether you first map the vector and then scale it: $f(\lambda a)=\lambda f(a)$ .

Image and core

Two sets important in considering linear mappings are the image and the kernel of a linear mapping $f\colon V \to W$ .

The image $\mathrm {im} (f)$ the mapping is the set of image vectors under , that is, the set of all with from . Therefore, the image set is also notated by The image is a subvector space of .

The kernel $\mathrm{ker}(f)$ the mapping is the set of vectors from , which are mapped by to the zero vector of It is a subvector space of . The mapping is injective exactly if the kernel contains only the zero vector.

Properties

A linear mapping between the vector spaces and maps the zero vector of to the zero vector of
, because $f\left(0_{V}\right)=f\left(0\cdot 0_{V}\right)=0\cdot f\left(0_{V}\right)=0_{W}.$
A relation between kernel and image of a linear mapping $f\colon V\to W$ is described by the homomorphism : The factor space $V / \mathrm {ker} (f)$ is isomorphic to the image $\mathrm{im}(f)$ .

Linear mappings between finite dimensional vector spaces.

Base

A linear mapping between finite-dimensional vector spaces is uniquely determined by the images of the vectors of a basis. If the vectors form $b_1, \dotsc, b_n$ a basis of the vector space and are $w_1, \dotsc, w_n$ vectors in , then there exists exactly one linear mapping $f\colon V\to W$ , which maps $b_{1}$ to w_1 , b_2 on $w_{2}$ , ..., b_{n}} $b_{n}$ w_n maps to If is any vector from , then it can be uniquely represented as a linear combination of the basis vectors:

$v = \textstyle\sum\limits_{j=1}^n v_j b_j$

Here are $v_{1},\ldots ,v_{n}$ the coordinates of the vector with respect to the basis $\{b_{1},\dotsc ,b_{n}\}$ . Its image f(v) is given by

$f(v)=\textstyle \sum \limits _{{j=1}}^{n}v_{j}f(b_{j})=\sum \limits _{{j=1}}^{n}v_{j}w_{j}.$

The mapping is injective if and only if the image vectors $w_1, \dotsc, w_n$ the basis are linearly independent. It is surjective if and only if $w_1, \dotsc, w_n$ span the target space

If one assigns to each element $b_1, \dotsc, b_n$ a basis of vector $w_1, \dotsc, w_n$ from arbitrarily, then one can use the above formula to continue this assignment uniquely to a linear mapping $f\colon V\to W$ .

Representing the image vectors w_j with respect to a basis of leads to the matrix representation of the linear mapping.

Mapping matrix

→ Main article: Mapping matrix

If and are finite dimensional, $\dim V = n$ , $\dim W = m$ , and are bases $B = \{b_1, \dotsc, b_n\}$ of and $B' = \{b_1', \dotsc, b_m'\}$ of given, then any linear mapping $f\colon V\to W$ $M^B_{B'}(f)$ be represented by an $m\times n$ matrix This is obtained as follows: For each basis vector $b_{j}$ from the image vector $b_1', \dotsc, b_m'$ represented f(b_j) as a linear combination of the basis vectors

$f(b_j) = \sum_{i=1}^m a_{ij} b_i'$

The $a_{ij}$ , $i = 1, \dotsc, m$ , $j = 1, \dotsc, n$ form the entries of the matrix $M^B_{B'}(f)$ :

$M^B_{B'}(f) = \begin{pmatrix} a_{11} & \dots & a_{1j} & \dots & a_{1n} \\ \vdots & & \vdots & & \vdots \\ a_{m1} & \dots &a_{mj} & \dots & a_{mn} \end{pmatrix}$

Thus, in the -th column are the coordinates of f(b_j) respect to the base .

Using this matrix, one can $v = v_1 b_1 + \dotsb + v_n b_n \in V$ calculate the image vector f(v) of each vector

$f(v) = \sum_{j=1}^n v_j f(b_j) = \sum_{j=1}^n v_j \left(\sum_{i=1}^m a_{ij} b_i' \right) = \sum_{i=1}^m \left(\sum_{j=1}^n a_{ij} v_j \right)b_i'$

Thus, for the coordinates $w_{1},\dotsc ,w_{m}$ of with respect to f(v) following holds true

$w_i = \sum_{j =1}^n a_{ij} v_j$ .

This can be expressed using matrix multiplication:

${\begin{pmatrix}w_{1}\\\vdots \\w_{m}\end{pmatrix}}={\begin{pmatrix}a_{{11}}&\dots &a_{{1n}}\\\vdots &&\vdots \\a_{{m1}}&\dots &a_{{mn}}\end{pmatrix}}\,{\begin{pmatrix}v_{1}\\\vdots \\v_{n}\end{pmatrix}}$

The matrix $M^B_{B'}(f)$ is called the mapping matrix or representation matrix of . Other notations for $M^B_{B'}(f)$ are $_{B'}f_B$ and $_{B'}[f]_B$ .

Dimension formula

→ Main article: Rank set

Image and core are related by the dimension theorem. This states that the dimension of is equal to the sum of the dimensions of the image and the core:

$\dim V=\dim \mathrm {ker} (f)+\dim \mathrm {im} (f)$

Summary of the properties of injective and surjective linear mappings

Linear mappings between infinite-dimensional vector spaces.

→ Main article: Linear operator

Especially in functional analysis one considers linear mappings between infinite-dimensional vector spaces. In this context, the linear mappings are usually called linear operators. The considered vector spaces usually carry the additional structure of a normalized complete vector space. Such vector spaces are called Banach spaces. In contrast to the finite dimensional case, it is not sufficient to study linear operators only on one basis. According to the Bairean category theorem, a basis of an infinite-dimensional Banach space has overcountably many elements and the existence of such a basis cannot be justified constructively, that is, only by using the axiom of selection. Therefore, one uses a different notion of bases, such as orthonormal bases or, more generally, Schauder bases. With this, certain operators such as Hilbert-Schmidt operators can be represented with the help of "infinite matrices", in which case infinite linear combinations must also be allowed.

Special linear mappings

Monomorphism

A monomorphism between vector spaces is a linear mapping $f\colon V\to W$ , which is injective. This is true exactly if the column vectors of the representation matrix are linearly independent.

Epimorphism

An epimorphism between vector spaces is a linear mapping $f\colon V\to W$ , which is surjective. This is the case exactly if the rank of the representation matrix is equal to the dimension of

Isomorphism

An isomorphism between vector spaces is a linear mapping $f\colon V\to W$ , which is bijective. This is exactly the case if the representation matrix is regular. The two spaces and then called isomorphic.

Endomorphism

An endomorphism between vector spaces is a linear mapping where the spaces and equal: $f\colon V\to V$ . The representation matrix of this mapping is a square matrix.

Automorphism

An automorphism between vector spaces is a bijective linear mapping where the spaces and are equal. Thus, it is both an isomorphism and an endomorphism. The representation matrix of this mapping is a regular matrix.

Vector space of linear mappings

The set L(V,W) of linear mappings from a -vector space to a -vector space is a vector space over , more precisely: a subvector space of the -vector space of all mappings from to . This means that the sum of two linear mappings and , component-wise defined by

$(f+g)\colon x\mapsto f(x)+g(x),$

is again a linear mapping and that the product

$(\lambda f) \colon x \mapsto \lambda f(x)$

of a linear mapping with a scalar λ $\lambda \in K$ is also a linear mapping again.

If has dimension and dimension and if a base and a base the mapping is

$L(V,W)\to K^{{m\times n}},\ f\mapsto M_{C}^{B}(f)$

into the matrix space $K^{m\times n}$ is an isomorphism. Thus the vector space L(V,W) has dimension $m \cdot n$ .

If we consider the set of linear self-mappings of a vector space, i.e. the special case V=W , these form not only a vector space, but with the concatenation of mappings as multiplication, an associative algebra, L(V) denoted briefly by

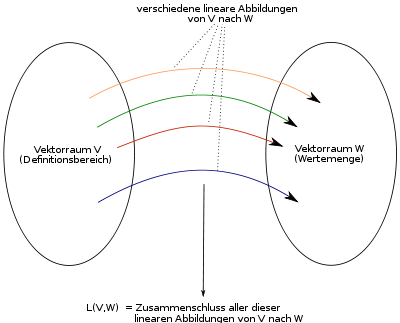
Formation of the vector space L(V,W)

Generalization

A linear mapping is a special case of an affine mapping.

Replacing the body by a ring in the definition of the linear mapping between vector spaces, we obtain a moduli homomorphism.