Linear independence

In linear algebra, a family of vectors of a vector space is called linearly independent if the zero vector can only be generated by a linear combination of the vectors in which all coefficients of the combination are set to the value zero. Equivalently (unless the family consists only of the zero vector), none of the vectors can be represented as a linear combination of the other vectors in the family.

Otherwise they are called linearly dependent. In this case, at least one of the vectors (but not necessarily each) can be represented as a linear combination of the others.

For example, in the three-dimensional Euclidean space $\mathbb {R} ^{3}$ the vectors (1,0,0) , (0,1,0) and (0,0,1) linearly independent. The vectors (2,{-1},1) (1,0,1) and (3,{-1},2) , on the other hand, are linearly dependent because the third vector is the sum of the first two, i.e. the difference between the sum of the first two and the third is the zero vector. The vectors (1,2,{-3}) , ({-2},{-4},6) and (1,1,1) are $2\cdot (1,2,{-3})+({-2},{-4},6)=(0,0,0)$ also linearly dependent because of but here the third vector cannot be represented as a linear combination of the other two.

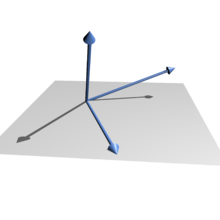
Linear independent vectors in ℝ3

Linear dependent vectors in a plane in ℝ3

Definition

Let be a vector space over the body and an index set. A family indexed by $({\vec {v}}_{i})_{i\in I}$ is called linearly independent if every finite subfamily contained in it is linearly independent.

A finite family ${\vec {v}}_{1},{\vec {v}}_{2},\dots ,{\vec {v}}_{n}$ of vectors from is called linearly independent if the only possible representation of the zero vector is as a linear combination

$a_{1}{\vec {v}}_{1}+a_{2}{\vec {v}}_{2}+\dotsb +a_{n}{\vec {v}}_{n}={\vec {0}}$

with coefficients $a_{1},a_{2},\dots ,a_{n}$ from the basic body is the one where all coefficients $a_{i}$ equal to zero. If, on the other hand, the zero vector can also be generated non-trivially (with coefficients not equal to zero), then the vectors are linearly dependent.

The family $({\vec {v}}_{i})_{i\in I}$ is thus linearly dependent if and only if there $J\subseteq I$ exists a finite non-empty subset and coefficients $(a_{j})_{j\in J}$ at least one of which is not equal to 0, so that

$\sum _{j\in J}a_{j}{\vec {v}}_{j}={\vec {0}}.$

The zero vector ${\vec {0}}$ is an element of the vector space . In contrast, 0 is an element of the body .

The term is also used for subsets of a vector space: A subset $S\subseteq V$ of a vector space is called linearly independent if every finite linear combination of pairwise different vectors from can represent the zero vector only if all coefficients in this linear combination have the value zero. Note the following difference: if, for example, $({\vec {v}}_{1},{\vec {v}}_{2})$ is a linearly independent family, then $({\vec {v}}_{1},{\vec {v}}_{1},{\vec {v}}_{2})$ obviously a linearly dependent family. However, the set $\{{\vec {v}}_{1},{\vec {v}}_{1},{\vec {v}}_{2}\}=\{{\vec {v}}_{1},{\vec {v}}_{2}\}$ is then linearly independent.

Other characterisations and simple properties

The vectors ${\vec {v}}_{1},\ldots ,{\vec {v}}_{n}$ are (unless and ${\vec {v}}_{1}={\vec {0}}$ ) are linearly independent exactly when none of them can be represented as a linear combination of the others.
This statement does not apply in the more general context of moduli over rings.

A variant of this statement is the dependence lemma: If ${\vec {v}}_{1},\ldots ,{\vec {v}}_{n}$ are linearly independent and ${\vec {v}}_{1},\ldots ,{\vec {v}}_{n},{\vec {w}}$ linearly dependent, then ${\vec {w}}$ as a linear combination of ${\vec {v}}_{1},\ldots ,{\vec {v}}_{n}$ .

If a family of vectors is linearly independent, then each subfamily of this family is also linearly independent. If, on the other hand, a family is linearly dependent, then every family that contains this dependent family is also linearly dependent.

Elementary transformations of the vectors do not change the linear dependence or the linear independence.

If the zero vector is one of the ${\vec {v}}_{i}$ (here: let ${\vec {v}}_{j}={\vec {0}}$ ), they are linearly dependent - the zero vector can be generated by $a_{i}=0$ setting all except for $a_{j}$ which, as a coefficient of the zero vector ${\vec {v}}_{j}$ may be arbitrary (i.e. in particular also non-zero).

In a -dimensional space, a family of more than vectors is always linearly dependent (see barrier lemma).

Determination by means of determinant

If one has given an -dimensional vector space as row or column vectors with respect to a fixed basis, one can check their linear independence by combining these row or column vectors into an $n\times n$ matrix and then calculating its determinant. The vectors are linearly independent if the determinant is not equal to 0.

Basis of a vector space

→ Main article: Basis (vector space)

The concept of linearly independent vectors plays an important role in the definition and handling of vector space bases. A base of a vector space is a linearly independent generating system. Bases make it possible to calculate with coordinates, especially for finite-dimensional vector spaces.

Examples

Single vector

${\vec {v}}$ Let the vector be an element of the vector space over . Then the single vector $\mathbf {v}$ linearly independent by itself exactly if it is not the zero vector.

For it follows from the definition of the vector space that if

$a\,\mathbf {v} =0$ with $a\in K$ , $\mathbf {v} \in V$

can only be a=0 or $\mathbf {v} =\mathbf {0}$ !

Vectors in the plane

The vectors $\mathbf {u} ={\begin{pmatrix}1\\1\end{pmatrix}}$ and $\mathbf {v} ={\begin{pmatrix}-3\\2\end{pmatrix}}$ are linearly independent in $\mathbb {R} ^{2}$ linearly independent.

Proof: For $a,b\in \mathbb {R}$ hold

$a\,\mathbf {u} +b\,\mathbf {v} =\mathbf {0} ,$

i.e.

$a\,{\begin{pmatrix}1\\1\end{pmatrix}}+b\,{\begin{pmatrix}-3\\2\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}}$

Then applies

${\begin{pmatrix}a-3b\\a+2b\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}},$

$a-3b=0\ \wedge \ a+2b=0.$

This system of equations is only valid for the solution a=0 , b=0 (the so-called trivial solution); i.e. and are linearly independent.

Standard basis in n-dimensional space

In the vector space $V=\mathbb {R} ^{n}$ consider the following elements (the natural or standard basis of ):

$\mathbf {e} _{1}=(1,0,0,\dots ,0)$

$\mathbf {e} _{2}=(0,1,0,\dots ,0)$

$\dots$

$\mathbf {e} _{n}=(0,0,0,\dots ,1)$

Then the vector family $(\mathbf {e} _{i})_{i\in I}$ with is $I=\{1,2,\dots ,n\}$ linearly independent.

Proof: For $a_{1},a_{2},\dots ,a_{n}\in \mathbb {R}$ apply

$a_{1}\,\mathbf {e} _{1}+a_{2}\,\mathbf {e} _{2}+\dotsb +a_{n}\,\mathbf {e} _{n}=\mathbf {0} .$

But then also

$a_{1}\,\mathbf {e} _{1}+a_{2}\,\mathbf {e} _{2}+\dots +a_{n}\,\mathbf {e} _{n}=(a_{1},a_{2},\ \dots ,a_{n})=\mathbf {0} ,$

and it follows that $a_{i}=0$ for all $i\in \{1,2,\dots ,n\}$ .

Functions as vectors

Let be the vector space of all functions $f\colon \mathbb {R} \to \mathbb {R}$ . The two functions $\mathrm {e} ^{t}$ and $\mathrm {e} ^{2t}$ in are linearly independent.

Proof: Let $a,b\in \mathbb {R}$ and let it hold

$a\,\mathrm {e} ^{t}+b\,\mathrm {e} ^{2t}=0$

for all $t\in \mathbb {R}$ . If one derives this equation according to , then one obtains a second equation

$a\,\mathrm {e} ^{t}+2b\,\mathrm {e} ^{2t}=0$

By subtracting the first equation from the second equation, we obtain

$b\,\mathrm {e} ^{2t}=0$

Since this equation must hold t=0 for all and thus in particular also for follows by substituting t=0 that b=0 must be. Substituting the calculated in this way back into the first equation yields

$a\,\mathrm {e} ^{t}+0=0$

It follows again that (for t=0 ) a=0 must be.

Since the first equation is only solvable for a=0 and b=0 , the two functions $\mathrm {e} ^{t}$ and $\mathrm {e} ^{2t}$ linearly independent.

Rows

Let be the vector space of all real-valued continuous functions $f\colon (0,1)\to \mathbb {R}$ on the open unit interval. Then it is true that

${\frac {1}{1-x}}=\sum _{n=0}^{\infty }x^{n},$

but nevertheless are ${\tfrac {1}{1-x}},1,x,x^{2},\ldots$ linearly independent. Linear combinations of powers of are in fact only polynomials and not general power series, so in particular they are restricted near 1, so that ${\tfrac {1}{1-x}}$ be represented as a linear combination of powers.

Rows and columns of a matrix

Another interesting question is whether the rows of a matrix are linearly independent or not. Here, the rows are regarded as vectors. If the rows of a square matrix are linearly independent, the matrix is called regular, otherwise singular. The columns of a square matrix are linearly independent exactly when the rows are linearly independent. Example of a sequence of regular matrices: Hilbert matrix.

Rational independence

Real numbers that are linearly independent over the rational numbers as coefficients are called rationally independent or incommensurable. The numbers $\lbrace 1,\,{\tfrac {1}{\sqrt {2}}}\rbrace$ are therefore rationally independent or incommensurable, the numbers $\lbrace 1,\,{\tfrac {1}{\sqrt {2}}},1+{\sqrt {2}}\rbrace$ on the other hand are rationally dependent.

Generalisations

The definition of linearly independent vectors can be applied analogously to elements of a module. In this context, linearly independent families are also called free (see also: free module).

The notion of linear independence can be further generalised to a consideration of independent sets, see Matroid.