Linear function (calculus)

This article is about functions in elementary calculus. For linear functions in linear algebra, see Linear mapping.

A linear function is often called (especially in school mathematics) a function $f\colon \mathbb {R} \to \mathbb {R}$ of the form

$f(x)=m\cdot x+n;\quad m,n\in \mathbb {R} ,$

i.e. a polynomial function of at most first degree.

However, this is not a linear mapping in the sense of linear algebra, but an affine mapping, since the linearity condition is generally not fulfilled. This is why it is also referred to as an affine-linear function. It is a linear mapping or linear function in the sense of linear algebra only in the special case , n=0 so $f(x)=mx.$ Such functions are also called homogeneous linear functions or proportional functions. Following this name, the function for the case is $n\neq 0$ also called a general linear function or a linear-inhomogeneous function. In this article, the frequently used term linear function is retained.

Linear functions are among the relatively simple functions in mathematics. They are continuous and differentiable. Many problems can be easily solved for linear functions; therefore, one often tries to approximate complicated problems by linear relationships.

Graph

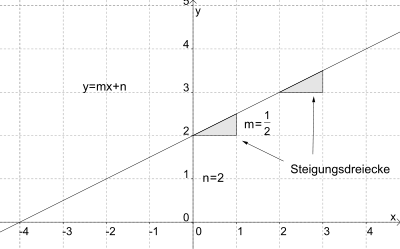
The graph of a linear function is a straight line. In Cartesian coordinates following applies (x|y)

$y=m\cdot x+n$

with real numbers and where (the abscissa) is an independent variable and (the ordinate) is the dependent variable.

There are numerous other naming conventions for the function term, such as ax+b, mx+c, mx+b or mx+t. In Austria, y=kx+d is often used, but in Switzerland, y=mx+q. In Belgium, one also finds y=mx+p or y=kx+t.

This representation is also called the normal form of a linear function. Its two parameters can be interpreted as follows:

The number indicates the slope of the line.
The number is the y-axis or ordinate intercept, inhomogeneity, or displacement constant.

The graph of a linear function is never parallel to the y-axis, because this would mean that one would have more than one associated with it, which would contradict the definitionally required (right-)uniqueness of a function.

Slope triangles on the graph of the linear function $x\mapsto {\tfrac {1}{2}}x+2$

Determination of the function term from two points

It is assumed that the points $(x_{1}|y_{1})$ and lie $(x_{2}|y_{2})$ on the graph of the linear function and are distinct from each other.

The slope can be calculated with

$m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}.$

The y-axis intercept is given by

$n=y_{1}-m\cdot x_{1}$ or $n=y_{2}-m\cdot x_{2}.$

The function term f(x) is given by

$f(x)={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot x+\left(y_{1}-{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot x_{1}\right)$

or more simply by

$f(x)={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot (x-x_{1})+y_{1}.$

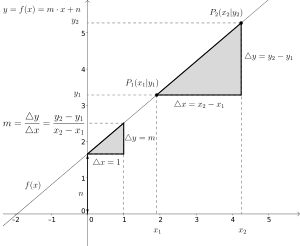
Slope of a linear function through two given points

Questions and Answers

Q: What is a linear function in basic mathematics?

A: A linear function in basic mathematics is a function whose graph is a straight line in 2-dimensions (2D).

Q: Can you provide an example of a linear function?

A: An example of a linear function is y=2x-1.

Q: What does a linear function refer to in higher mathematics?

A: In higher mathematics, a linear function often refers to a linear mapping.

Q: Is a linear function always represented by a straight line?

A: Yes, a linear function is always represented by a straight line.

Q: Can a linear function have multiple solutions?

A: No, a linear function can have only one solution because it is a straight line.

Q: Is y=3x+2 a linear function?

A: Yes, y=3x+2 is a linear function because its graph is a straight line.

Q: In how many dimensions is the graph of a linear function represented?

A: The graph of a linear function is represented in 2 dimensions (2D).