Linear equation

This article discusses linear equations in linear algebra; for linear equations in analytic geometry, see straight line equation.

A linear equation is a mathematical equation of determination in which only linear combinations of the unknowns occur. Characteristic for a linear equation is that each unknown is only in the first power, i.e. it is not squared (see quadratic equation). Typically, the unknowns of a linear equation are scalars, usually real numbers. In the simplest case of a scalar unknown a linear equation has the form

$a \cdot x = b$ ,

where and are constants. However, there are also linear equations with several unknowns and with other mathematical objects as unknowns, for example sequences (linear difference equations), vectors (linear systems of equations) or functions (linear differential equations). In the general case, a linear equation has the form

T(x) = b ,

where is a linear mapping.

Homogeneous linear equations are special linear equations where the constant term of the equation is zero. The solutions of a homogeneous linear equation form a subvector space of the vector space of unknowns and thus possess special properties such as the validity of the superposition principle. The solutions of an inhomogeneous linear equation, on the other hand, form an affine subspace, so each solution of an inhomogeneous linear equation can be represented as the sum of the solution of the associated homogeneous equation and a particular solution. The solution space of a linear equation can be characterized by the kernel and the kokernel of the linear mapping.

Linear equations and their solutions are studied especially in linear algebra and linear functional analysis, but they also play a role in number theory.

Scalar linear equations

Often the unknowns in linear equations are scalars (mostly real or complex numbers). Such linear equations are then special algebraic equations of degree 1.

Linear equations with one unknown

A scalar equation with one unknown is called linear if it can be transformed by equivalent transformations (see Solving Equations) into the form

$a \cdot x = b$

can be brought. Here, and are are constants which do not depend on

If $a\neq 0$ , the value of the unknown , with which the equation is satisfied, can be determined by dividing on both sides by

$x = \frac{b}{a}$

If a=0 and $b\neq 0$ , the equation has no solution. If a=0 and b=0 , there are infinitely many solutions, because then every satisfies the equation.

Examples

The solution of the linear equation

$3 \cdot x = 24$

is obtained by dividing both sides by 3, so that on the left side only the unknown remains:

$x = \frac{24}{3} = 8$ .

The linear equation

$0 \cdot x = 7$

has no solution, while the linear equation

$0 \cdot x = 0$

is satisfied for each

Linear equations with two unknowns

A scalar equation with two unknowns and is called linear if it can be transformed by equivalent transformations into the form

$a \cdot x + b \cdot y = c$

where and are constants. The solutions form straight lines in two-dimensional space unless both a=0 and b=0 hold. One speaks then also of the coordinate form of a straight line equation. Otherwise the solution set is either the whole two-dimensional space (c=0) or empty $(c \neq 0)$ .

The solution of such an equation is often given in parameter representation. To do this, one solves the equation according to one of the unknowns, for example , which, provided $b \neq 0$ ,

$y = (c - a \cdot x) / b$

and takes the other unknown as a free parameter . Thus, the solution can be written as

and x = t with $y = (c - a \cdot t) / b$ $t \in \mathbb{R}$

in the equation. In this way it becomes visible that, although the equation contains two unknowns, the solution space is only one-dimensional, i.e. it depends only on one parameter The parameter representation itself is not unique. If $a\neq 0$ , one can also resolve the equation to and choose as a free parameter. Other parameterizations are also possible, nevertheless the same solution set is described by them.

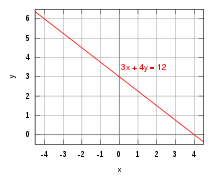
Example

The solution set for the linear equation

$3 \cdot x + 4 \cdot y = 12$

is obtained by resolving to as

and x = t with $y = (12 - 3 \cdot t)/4$ $t \in \mathbb{R}$

is given. The function graph of the described straight line is then obtained via the straight line equation

$f(x) = (12 - 3 \cdot x)/4 = -(3/4) \cdot x + 3$ .

Linear equations with several unknowns

In general, a scalar equation with unknowns $x_1, x_2, \dotsc, x_n$ called linear if it can be transformed by equivalent transformations into the form

$a_{1}x_{1}+a_{2}x_{2}+\dotsb +a_{n}x_{n}=b$

where $a_{1},a_{2},\dotsc ,a_{n}$ and are constants. Thus, only linear combinations of the unknowns may occur. The solutions of such equations are in general (n-1) -dimensional subsets (hyperplanes) of the corresponding -dimensional space. If $a_{1}=a_{2}=\dotsb =a_{n}=0$ solution set is either the whole -dimensional space (b = 0) or empty $(b \neq 0)$ .

The parameter representation of the solution set is again obtained in the general case by solving the equation for one of the unknowns, for example $x_{n}$ if $a_n \neq 0$ , resolves,

$x_n = (b - a_1 x_1 -\;\cdots \; - a_{n-1} x_{n-1})/a_n$ ,

and the other unknowns as free parameters $t_{1}$ to $t_{n-1}$ . Thus the solution set is given as

with $x_{1}=t_{1},\dotsc ,x_{n-1}=t_{n-1},x_{n}=(b-a_{1}t_{1}-\dotsb -a_{n-1}t_{n-1})/a_{n}$ $t_{1},\dotsc ,t_{n-1}\in \mathbb {R}$ .

Because n-1 parameters are freely selectable, the solution space (n-1) -dimensional. Again, the parameter representation is not unique, one can also solve the equation for one of the other unknowns, provided the associated coefficient is not zero, or choose a different parameterization.

Example

The solution set of the linear equation with three unknowns

$3\cdot x_{1}+2\cdot x_{2}+x_{3}=7$

is a plane in three-dimensional space with representation

with $x_1 = t_1, \; x_2 = t_2, \; x_3 = 7 - 3 \cdot t_1 - 2 \cdot t_2$ $t_1, t_2 \in \mathbb{R}$ .

The solution set of the linear equation $3x+4y=12$

The solution of a real linear equation with three unknowns is generally a plane.

General linear equations

Linear mappings

In general, linear equations are defined in terms of linear mappings. An equation of the form

T(x) = b

is called linear if a linear mapping and if is independent of The mapping $T\colon V\to W$ thereby maps from a vector space into a vector space where $x\in V$ and $b\in W$ defined over a common body A mapping is linear if for constants λ $\lambda, \mu \in K$

$T\left(\lambda x + \mu y\right) = \lambda T\left( x \right) + \mu T\left( y\right)$

applies.

Example

If $V = \mathbb{R}^n$ and $W = \mathbb{R}$ , then $x=(x_{1},\dotsc ,x_{n})\in \mathbb {R} ^{n}$ a real vector and $b \in \mathbb{R}$ is a real number. If we now choose for the linear mapping

$T(x) = a \cdot x$

with constant vector $a=(a_{1},\dotsc ,a_{n})\in \mathbb {R} ^{n}$ , where $( \cdot )$ is the standard scalar product of the two vectors, then we obtain the linear vector equation

$a \cdot x = b$ ,

which is equivalent to the above scalar linear equation with unknowns. The linearity of follows directly from the linearity of the scalar multiplication

$T(\lambda x+\mu y) = a \cdot (\lambda x+\mu y) = \lambda(a \cdot x)+\mu(a \cdot y) = \lambda T(x)+\mu T(y)$ .

Homogeneity

A linear equation is called homogeneous if b=0 , i.e. if it has the form

T(x) = 0

otherwise a linear equation is called inhomogeneous. Homogeneous linear equations have at least the zero vector

x=0

as a solution, since

$T(0) = T(0 \cdot 0) = 0 \cdot T(0) = 0$

holds. Conversely, inhomogeneous linear equations are never satisfied by the trivial solution.

Example

The solution of the homogeneous linear equation with two unknowns $x_{1}$ and $x_{2}$

$3x_{1}+4x_{2}=0$

is a straight line in two-dimensional space passing through the zero point. The solution of the inhomogeneous equation

$3x_{1}+4x_{2}=12$

is a straight line parallel to it, but it does not contain the zero point.

Superposition

→ Main article: Superposition (mathematics)

Homogeneous linear equations have the superposition property: If $\hat{x}$ and ${\bar {x}}$ two solutions of a homogeneous linear equation, then is also $\hat{x}+\bar{x}$ a solution of this equation. In general, it is even true that all linear combinations $c\hat{x}+d\bar{x}$ of solutions of a homogeneous linear equation with constants and solve this equation, since

$T(c\hat{x}+d\bar{x}) = T(c\hat{x})+T(d\bar{x}) = cT(\hat{x}) + dT(\bar{x}) = 0 + 0 = 0$

holds. By including x=0 and the superposition property, the solutions of a homogeneous linear equation form a subvector space of .

Furthermore, the solution of an inhomogeneous equation can be represented as the sum of the solution of the associated homogeneous equation and a particular solution: Let ${\bar {x}}$ be a concrete solution of an inhomogeneous linear equation and let the general solution of the associated homogeneous problem, then is $y+\bar{x}$ the general solution of the inhomogeneous equation, since

$T(y+\bar{x}) = T(y) + T(\bar{x}) = 0 + b = b$

holds. The solutions of an inhomogeneous linear equation thus form an affine subspace over the vector space of the associated homogeneous equation.

Conversely, if $\hat{x}$ and are ${\bar {x}}$ two solutions of an inhomogeneous linear equation, then solves $\hat{x} - \bar{x}$ the corresponding homogeneous equation, since

$T(\hat{x}-\bar{x}) = T(\hat{x}) - T(\bar{x}) = b - b = 0$

applies.

Example

A concrete solution of the inhomogeneous equation

x_1 - 2 x_2 = 10

$\bar{x}_1 = 4, \bar{x}_2 = -3$ .

Now, if are y = (y_1, y_2) the solutions of the corresponding homogeneous equation

y_1 - 2 y_2 = 0 ,

so all with y_1 = 2 y_2 , then the inhomogeneous equation is generally solved by

with $x = y + \bar{x} = (y_1 + \bar{x}_1, y_2 + \bar{x}_2) = (2 y_2 + 4, y_2 - 3) = (2t + 4, t - 3)$ $t \in \mathbb{R}$ .

Dimension of the solution space

The solution space of a homogeneous linear equation is called the kernel $\mathrm{ker}(T)$ the linear mapping, its dimension is also called the defect. Due to the rank theorem, the dimension of the solution space of a finite-dimensional homogeneous linear equation is

$\mathrm{dim}(\mathrm{ker}(T)) = \dim(V) - \mathrm{rang}(T)$ .

Here $\mathrm{rang}(T)$ the rank of the mapping, i.e. the dimension of its image. The image of a mapping is the set of values that T(x) $x\in V$ can take for

Due to the superposition property, the dimension of the solution space of an inhomogeneous linear equation is equal to that of the corresponding homogeneous equation, provided that a particular solution exists. This is the case exactly if the right-hand side the image of the mapping, i.e., $b \in T(V)$ holds. The coker of the linear mapping $\mathrm{coker}(T)=W / T(V)$ describes just the space of conditions that the right-hand side of a linear equation must satisfy for the equation to be solvable. Its dimension is

$\mathrm{dim}(\mathrm{coker}(T)) = \mathrm{dim}(W) - \mathrm{rang}(T)$ .

Examples

If we choose as vector spaces $V = \mathbb{R}^3$ and $W = \mathbb{R}$ and as a linear mapping

T(x) = a_1x_1 + a_2x_2 + a_3x_3 ,

where at least one of the coefficients is a_1, a_2, a_3 nonzero, then the image of the whole space and thus

$\mathrm{dim}(\mathrm{ker}(T)) = \dim(\mathbb{R}^3) - \dim(\mathbb{R}) = 3 - 1 = 2$ .

Thus, the solution space of the homogeneous linear equation T(x)=0 has dimension 2 and is a plane in three-dimensional space. The solution space of the inhomogeneous equation T(x)=b is also a plane here, since if, for example, $a_1 \neq 0$ , the equation has the particle solution (b/a_1, 0, 0) The cokernel here has dimension 0, so the equation is solvable for any

If you choose instead

T(x) = 0x_1 + 0x_2 + 0x_3 ,

then all vectors from are mapped to the zero and the following applies

$\mathrm{dim}(\mathrm{ker}(T)) = \dim(\mathbb{R}^3) - \dim(\{ 0 \}) = 3 - 0 = 3$ .

The solution space of the corresponding homogeneous linear equation is therefore the entire three-dimensional space. The solution space of the inhomogeneous equation is empty in this case, since the equation has a solution only for b=0 The cokernel has dimension 1.

Linear equation

Scalar linear equations

Linear equations with one unknown

Linear equations with two unknowns

Linear equations with several unknowns

General linear equations

Linear mappings

Homogeneity

Superposition

Dimension of the solution space

Search by letter