Limit of a sequence

The limit of a sequence of numbers is a number to which the members of the sequence come arbitrarily close, in such a way that almost all the members of the sequence lie in each vicinity of the limit. If a sequence has such a limit, it is said to be convergent; otherwise it is said to be divergent. An example of a convergent sequence is $a_{n}={\tfrac {1}{n}}$ , as n increases it approaches 0, so this is its limit. Such a sequence is also called a zero sequence. The constant sequence $a_{n}=c$ also converges, its limit is just the number . On the other hand, the sequence $a_{n}=(-1)^{n}$ , since it does not just approximate a number, but alternates ("jumps back and forth") between the two values -1 and 1. The limit of the sequence of partial sums of a series is called the limit of the series for short; convergence and divergence of a series are defined accordingly.

The limit of a sequence is defined not only for sequences of numbers, but just as well for sequences, whose members belong to a metric space, i.e. that between them a real valued distance is defined. In a further generalization a topological space is sufficient too; there the notion of environment, which is used here, can be defined without metric too. See the sections Limit of a sequence of elements of a metric space and of a topological space.

Convergence is a fundamental concept in modern calculus. In a more general sense, it is treated in topology.

In ancient Greek philosophy and mathematics the concept of limit was not yet available, see for example Achilles and the tortoise. The modern formulation of the concept of limit value ("for every deviation, however small, there is a first index ...") first appeared in 1816 with Bernard Bolzano, later further formalized by Augustin-Louis Cauchy and Karl Weierstrass.

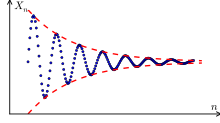
Example of a sequence that tends towards a limit value at infinity

Limit of a real number sequence

Explanation and definition

Each member $a_{n}$ of a sequence $(a_{n})_{n\in \mathbb {N} }$ real numbers has index . The number $a\in \mathbb{R}$ is the limit of this sequence if for every ε $\varepsilon >0$ all members with sufficiently large index "around " lie in the open interval $(a-\varepsilon ,a+\varepsilon )$ . So then also only finitely many sequence members lie outside the interval, and these all have a smaller index. The interval $(a-\varepsilon ,a+\varepsilon )$ is thereby the environment of the limit mentioned in the introductory text; more precisely, this is called the ε $\varepsilon$ -environment of a, and then $U_{\varepsilon }(a)$ written. The speech " $(a_{n})_{n\in \mathbb {N} }$ has limit a" and " $(a_{n})_{n\in \mathbb {N} }$ converges to a" are exactly equivalent.

This concretization can be well reconciled with the descriptive interpretation of convergence as "approximation to the limit": No matter how one $\varepsilon$ chooses the ε , above a certain index all members always lie in $(a-\varepsilon ,a+\varepsilon )$ , where its distance from is less than ε . $\varepsilon$ This gives the exact definition:

The number $a\in \mathbb{R}$ is called the limit of the sequence $(a_{n})_{n\in \mathbb {N} }$ , if for every ε $\varepsilon >0$ exists a natural number such that $\left|a_{n}-a\right|<\varepsilon$ , if $n\geq N.$

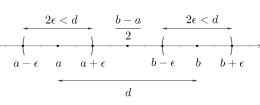
Thus, this definition requires: for every ε $\varepsilon >0$ , there exists an index with the property that all sequence members with index or greater less than ε $\varepsilon$ are away from .

This is to be understood in such a way that as ε $\varepsilon$ an arbitrarily small positive number may be given, and that it is then always possible to specify a sufficiently large such a way that $a_{N}$ and all following members satisfy the condition. We then say that almost all sequence members, that is, all but finitely many sequence members, satisfy the condition.

Note 1: If the convergence of a sequence is to be proved with this definition, the limit value must be known in advance. However, there are also criteria with which the convergence of a sequence can be proven without the limit value being known: see convergence criteria.

Note 2: The conspicuous (by the frequency of their use) designation of "small" numbers by the letter ε $\varepsilon$ has become generally accepted and is caricatured as epsilontics.

Illustration

Example of a sequence converging to the limit

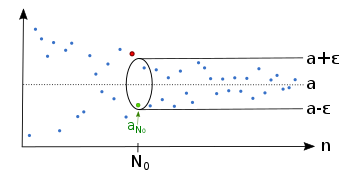
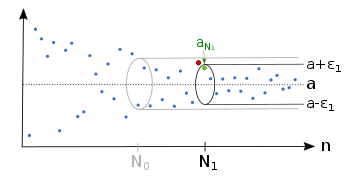
If we specify an ε $\varepsilon >0$ , there is a minimum index $N_{0}$ such that from this index onwards the sequence is in the epsilon hose . $(a-\varepsilon ,a+\varepsilon )$

Also, for a smaller ε $\varepsilon _{1}>0$ , there is a minimum index $N_{1}$ , after which the sequence is completely in the epsilon tube.

No matter which ε $\varepsilon >0$ we specify, only finitely many sequence members lie outside the epsilon hose $(a-\varepsilon ,a+\varepsilon )$ .

Uniqueness of the limit value

The limit of a sequence $(a_{n})$ , if it exists, is uniquely determined.

This statement follows directly from the definition by means of a proof of contradiction. If a sequence $(a_{n})$ had two different limits $a \neq b$ then these would have a distance $d=|a-b|>0$ . Now consider $\epsilon$ -environments with $\epsilon <{\tfrac {d}{2}}$ to the two limits, that is, in the real case, the intervals $(a-\epsilon ,a+\epsilon )$ and $(b-\epsilon ,b+\epsilon )$ , then these do not have a common point. However, by the definition of the limit, above a certain index all sequence members must lie in the $\epsilon$ -environment of the limit, and thus the $\epsilon$ -environments of and have infinitely many common points. This contradiction can only be resolved if and no positive distance, i.e. a=b holds.

Notation

For the limit of a sequence $(a_{n})_{n\in \mathbb {N} }$ there is a separate symbol, one writes: $\lim _{{n\to \infty }}a_{n}=a$ .

Besides this notation, the notation $a_{n}\to a$ for $n\to \infty$ , read as $a_{n}\;$ converges to $a\;$ for to infinity, or briefly $a_{n}\to a$ common.

With this notation, the definition of the limit of a sequence can be shortened: $\lim _{{n\to \infty }}a_{n}=a\quad \Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in {\mathbb {N}}\;\forall n\geq N:\;\left|a_{n}-a\right|<\varepsilon$ .

Using the ambient notation, the definition is: $\lim _{n\to \infty }a_{n}=a\quad \Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in \mathbb {N} \;\forall n\geq N:\;a_{n}\in U_{\varepsilon }(a)$ .

Examples

The definition of the limit value is to be made clear by means of an example, after which further limit values are listed.

To prove that the sequence ${\tfrac {1}{n}}$ $0$ converges to , choose $\varepsilon$ as some natural number to given ε {\displaystylewhich is greater than ${\tfrac {1}{\varepsilon }}$ (the existence of such an is ensured by Archimedes' axiom). Then for all $n\geq N$ :

$|a_{n}-0|={\frac {1}{n}}\leq {\frac {1}{N}}<\varepsilon$

The first inequality follows from $n\geq N$ , the second from $N>{\tfrac {1}{\varepsilon }}$ . Hereby the required existence of the index is shown, the number $0$ is limit of the sequence $a_{n}={\tfrac {1}{n}}$ .

Sequences that converge to zero, like this very example ${\tfrac {1}{n}}$ are called zero sequences.

The constant sequence with a fixed real number converges to .
The sequence $(1;1{,}4;1{,}41;1{,}414;1{,}4142;1{,}41421;\dotsc )$ of the terminating decimal fraction expansions of ${\sqrt {2}}$ converges to ${\sqrt {2}}$ .
The sequence $(e_{n})$ with $e_{n}=\left(1+{\tfrac {1}{n}}\right)^{n}$ is convergent to Euler's number . The sequence $\left(1+{\tfrac {r}{n}}\right)^{n}$ converges to $e^{r}$ . This sequence of numbers occurs in the continuous interest problem (see calculus of interest).
The sequence $(c_{n})$ with $c_{n}=(-1)^{n}+{\tfrac {1}{n}}$ is not convergent, but has two convergent subsequences for even and odd .

Calculation rules

The following calculation rules apply to limit values:

If the limit exists. $\lim _{{n\to \infty }}a_{n}=a$ , then for any $c\in \mathbb{R} \;$ the following limits also exist and can be computed as indicated:

$\lim _{{n\to \infty }}ca_{n}=ca,$
$\lim _{{n\to \infty }}\left(c+a_{n}\right)=c+a,$
$\lim _{{n\to \infty }}\left(c-a_{n}\right)=c-a.$

Additionally, if $a\neq 0$ then also $a_n\neq 0$ above some index $N_{0}\;$ and for the subsequence of $n>N_{0}\;$ holds

$\lim _{{n\to \infty }}{\frac {c}{a_{n}}}={\frac {c}{a}}.$

If the values lim $\lim _{{n\to \infty }}a_{n}=a$ and exist. $\lim _{{n\to \infty }}b_{n}=b$ , then the following limits also exist and can be computed as indicated:

$\lim _{{n\to \infty }}\left(a_{n}+b_{n}\right)=a+b,$
$\lim _{{n\to \infty }}\left(a_{n}-b_{n}\right)=a-b,$
$\lim _{{n\to \infty }}\left(a_{n}\cdot b_{n}\right)=a\cdot b.$

Additionally, if $b\neq 0$ , then also $b_{n}\neq 0$ above some index $N_{0}\;$ and for the subsequence of $n>N_{0}\;$ , then

$\lim _{{n\to \infty }}{\frac {a_{n}}{b_{n}}}={\frac {a}{b}}$ .

With the help of these calculation rules, in many cases further limit values can be easily calculated from known limit values. For example, for the limit of the sequence ${\tfrac {2n^{2}-1}{n^{2}+1}}$

$\lim _{{n\to \infty }}{\frac {2n^{2}-1}{n^{2}+1}}=\lim _{{n\to \infty }}{\frac {2-{\frac {1}{n^{2}}}}{1+{\frac {1}{n^{2}}}}}={\frac {\lim _{{n\to \infty }}\left(2-{\frac {1}{n^{2}}}\right)}{\lim _{{n\to \infty }}\left(1+{\frac {1}{n^{2}}}\right)}}={\frac {2-\lim _{{n\to \infty }}{\frac {1}{n^{2}}}}{1+\lim _{{n\to \infty }}{\frac {1}{n^{2}}}}}={\frac {2-0}{1+0}}=2.$

Boundary value of a bounded convergent sequence

Monotonicity is not assumed for the sequences considered here.

If a convergent sequence $(a_{n})$ real numbers has an upper bound σ $\sigma$ (i.e. for all $a_{n}$ holds: $a_{n}\leq \sigma$ ), then $\lim _{n\to \infty }a_{n}=a\leq \sigma$ .

(Indirect)Proof: Assume $a>\sigma$ . Then a $0<\epsilon =a-\sigma$ given, and for almost all $a_{n}$ holds (see above section "Explanation and Definition"):

$a_{n}>a-\epsilon =a-(a-\sigma )=\sigma$ (Contradiction).

If a convergent sequence $(a_{n})$ real numbers has a lower bound σ $\sigma$ (i.e. for all $a_{n}$ holds: $a_{n}\geq \sigma$ ), then $\lim _{n\to \infty }a_{n}=a\geq \sigma$ .

(Indirect)Proof: Assumption: $a<\sigma$ . Then a $0<\epsilon =\sigma -a$ given, and for almost all $a_{n}$ holds (see above section "Explanation and Definition"):

$a_{n}<a+\epsilon =a+(\sigma -a)=\sigma$ (contradiction).

Important limit values

$\lim _{{n\to \infty }}{\frac {1}{n}}=0$
$\lim _{{n\to \infty }}{\sqrt[ {n}]{n}}=1$
$\lim _{{n\to \infty }}\left(1+{\frac {z}{n}}\right)^{n}=e^{z}$ for complex (and thus especially for real) numbers .
$\lim _{{n\to \infty }}n(a^{{{\frac 1{n}}}}-1)=\ln a$ for real
$\lim _{n\to \infty }\left(\sum _{i=1}^{n}{\frac {1}{i}}-\ln n\right)=\gamma$ (Euler-Mascheroni constant)

Limit value formation and function evaluation

The calculation rules can be seen as a special case of the following laws:

If $f\colon \mathbb {R} \to \mathbb {R}$ continuous at the point and if $a_{n}$ converges to then

$\lim _{n\to \infty }f\left(a_{n}\right)=f\left(\lim _{n\to \infty }a_{n}\right)=f(a)$ ;

If $g\colon \mathbb{R} ^{2}\to \mathbb{R}$ continuous at the point and if $a_{n}$ converges to and $b_{n}$ converges to , then

$\lim _{n\to \infty }g\left(a_{n},b_{n}\right)=g\left(\lim _{n\to \infty }a_{n},\lim _{n\to \infty }b_{n}\right)=g(a,b)$ .

For continuous functions, therefore, limit value formation and function evaluation are interchangeable. The calculation rules given above thus follow directly from the continuity of addition, subtraction, multiplication and, if the denominator is not equal to zero, division.

In the real numbers, the converse also holds: if the function $f\colon \mathbb {R} \to \mathbb {R}$ is given and holds for all sequences $(a_{n})_{n\in \mathbb {N} }$ with $a_{n}\to a$ also $\lim _{n\to \infty }f\left(a_{n}\right)=f(a)$ , then is continuous at the point .

The corresponding holds for any function $g\colon \mathbb{R} ^{2}\to \mathbb{R}$ : For all sequences $(a_{n})_{n\in \mathbb {N} }$ , $\left(b_{n}\right)_{n\in \mathbb {N} }$ with $a_{n}\to a$ and $b_{n}\to b$ also $\lim _{{n\to \infty }}g\left(a_{n},b_{n}\right)=g(a,b)$ , then is continuous at the point (a,b) .

Convergence criteria

In the definition of convergence given above, the limit $a\;$ is used in the definition. Thus, the limit value must be known or at least suspected in order for this definition to prove the convergence of the sequence. However, there are also convergence criteria that can be used to prove the convergence of a sequence without knowing the limit.

The monotonicity criterion states that a monotonically growing sequence converges exactly when it is bounded above. The limit of the sequence is then less than or equal to the upper bound. Formally, then, holds:

$a_{n}\leq a_{{n+1}}{\text{ und }}a_{n}\leq A{\text{ für alle }}n\quad \Rightarrow \quad a_{n}{\text{ konvergiert und }}\lim _{{n\to \infty }}a_{n}\leq A$ .

Similarly, a monotonically decreasing and downward bounded sequence converges.

The Cauchy criterion is based on the notion of Cauchy sequence: sequence $(a_{n})_{{n\in {\mathbb {N}}}}$ is called a Cauchy sequence if holds:

$\forall \varepsilon >0\ \exists N\in \mathbb {N} :\ \forall n,m\in \mathbb {N} ,n\geq N,m\geq N:|a_{m}-a_{n}|<\varepsilon$ .

The Cauchy criterion now states that a sequence in the real numbers converges exactly if it is a Cauchy sequence. This criterion plays an important role in particular in the construction of the real numbers from the rational numbers and in the extension of the notion of limit to metric spaces.

Determination of limit values

Once the convergence of a sequence is proved, the limit can be approximated in many cases by substituting a large n into the sequence and estimating the remainder. For example, for the limit $\lim _{{n\to \infty }}\left(1+{\frac 1{n}}\right)^{n}=e$ because of the estimate $\left(1+{\frac 1{n}}\right)^{n}<e<\left(1+{\frac 1{n}}\right)^{{n+1}}$ for n=1000 the estimation $2{,}7169\dotso <e<2{,}7196\dotso$

However, there is no general procedure for the exact determination of limit values. In many cases, de l'Hospital's rule can be applied. Sometimes it is useful to convert the limit value into a certain integral. Often, however, only refined decompositions and transformations lead further.

Certain divergence

In the real numbers, we distinguish between definite divergence and indefinite divergence:

Certain divergence against $+\infty$ (or $-\infty$ ) exists if a sequence xn exceeds every real number at some point and then stays above it (or falls below every real number and then stays below it). That is,

$\forall M\in {\mathbb {R}}\ \exists N\in {\mathbb {N}}\quad \forall n>N:x_{n}>M$

respectively

$\forall M\in {\mathbb {R}}\ \exists N\in {\mathbb {N}}\quad \forall n>N:x_{n}<M$ .

One then writes

$\lim _{{n\to \infty }}x_{n}=\infty$

respectively

$\lim _{{n\to \infty }}x_{n}=-\infty$

and says the sequence certainly diverges against $\infty$ or against $-\infty$ . The values $\infty$ and $-\infty$ are often called improper limits in this context, respectively, the determinate divergence is called improper convergence. That these values are also regarded as limits in a somewhat broader sense is justified in that the improper limits in the extended real numbers ${\bar {\mathbb{R} }}:=\mathbb{R} \cup \{-\infty ,+\infty \}$ , provided with a suitable topology, are real limits in the sense of the general topological limit notion described below.

Indeterminate divergence occurs when the sequence neither converges nor diverges determinately.

Examples

The sequence of natural numbers diverges determined against $\infty$ .
The sequence $(+1;-1;+1;-1;\dotsc )$ diverges indefinitely.
The sequence $(1;-2;3;-4;5;-6;\dotsc )$ diverges indefinitely.

Limit value and accumulation point

A term closely related to the limit of a sequence is the clustering point or also the clustering value of a sequence. The formal definitions differ only in the position of the existential or all-quantors:

While the limit value as

$\left(\lim _{{n\to \infty }}a_{n}=a\right)\quad :\Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in {\mathbb {N}}\;\forall n>N:\;\left|a_{n}-a\right|<\varepsilon$

is defined, "only" the following applies to the accumulation point

$a\;$ is cluster point of $a_{n}:\Longleftrightarrow \quad \forall \varepsilon >0\;\forall N\in {\mathbb {N}}\;\exists n>N:\;\left|a_{n}-a\right|<\varepsilon$ .

Thus, the definition of limit requires that in each neighborhood of the limit, starting from a certain index, all sequence members lie; the definition of clustering point requires only that in each neighborhood infinitely many sequence members lie.

Analogous to the improper limits, the improper clustering points are occasionally defined:

$+\infty \;$ is improper cluster point of $a_{n}\Longleftrightarrow \forall M\in {\mathbb {R}}\ \forall N\in {\mathbb {N}}\quad \exists n>N:\quad x_{n}>M$ ,

$-\infty \;$ is improper cluster point of $a_{n}\Longleftrightarrow \forall M\in {\mathbb {R}}\ \forall N\in {\mathbb {N}}\quad \exists n>N:\quad x_{n}<M$ .

Also the definition of the improper clustering point differs from the definition of the improper limit only by the position of the existential or all-quantors.

If a sequence has a proper (or improper) limit, then this limit is also a proper (or improper) cluster point. But while a sequence has at most one limit, it can have several clustering points. For each proper (or improper) clustering point there is a subsequence that converges (or diverges) against this clustering point. Conversely, if a sequence contains a convergent (or definitely divergent) subsequence, then the (proper or improper) limit of this sequence is a (proper or improper) cluster point of the sequence.

According to the theorem of Bolzano-Weierstrass every bounded real sequence contains a convergent subsequence. If the sequence is unbounded upwards, it contains a subsequence $+\infty$ determined to be divergent towards , if it is unbounded downwards, it contains a $-\infty$ subsequence determined to be divergent towards Thus, every real sequence has at least one proper or improper clustering point. The largest of these clustering points is called the limes superior, the smallest the limes inferior. For a formal definition, see the article Limes superior and Limes inferior. If the limes superior and the limes inferior coincide, then this value is also the proper or improper limit and the sequence is convergent or definitely divergent. If the limes superior and the limes inferior are different, the sequence is indefinitely divergent.

Illustration of the limit value of a sequence

$(a-\epsilon ,a+\epsilon )\cap (b-\epsilon ,b+\epsilon )=\emptyset$

Limit of a rational number sequence

The limit of a sequence of rational numbers is formally defined like the limit of a sequence of real numbers:

$\left(\lim _{{n\to \infty }}a_{n}=a\right)\quad \Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in {\mathbb {N}}\;\forall n>N:\;\left|a_{n}-a\right|<\varepsilon$

While this is $\varepsilon \;$ not a particular restriction for $a_{n}\;$ and ε , it has a $a\;$ substantial effect for the limit Thus there is no rational number against which the above sequence (1, 1.4, 1.41, 1.414, 1.4142, 1.41421, ...) of truncating decimal fractions of √2 converges. The sequence is thus divergent in the rational numbers, even though it is both monotonically increasing and bounded, thus satisfying the monotonicity criterion, and a Cauchy sequence, thus also satisfying the Cauchy criterion. The rational numbers thus have "gaps".

These "gaps" were already known to Euclid in antiquity; but it was not until the 19th century that these "gaps" were successfully closed by the systematic introduction of the real numbers. A frequently used way of the systematic introduction of the real numbers is to first consider Cauchy sequences of rational numbers, to regard as equivalent those Cauchy sequences whose differences form a zero sequence, and, building on this, to define the real numbers as classes of equivalent sequences. In this extension of the number-range then the above given criterion of monotonicity and Cauchy hold; in particular that now every Cauchy-sequence is convergent.

Thus, to say whether a sequence converges, it is important to know which range of numbers is being considered; a sequence that is convergent in the real numbers may be divergent in the rational numbers. If nothing else is said, however, limit values above the real numbers are usually considered, since these are the more suitable model for most applications.