Laplace's equation

This article explains the differential equation. For the equation about the pressure conditions in liquids, see Young-Laplace equation.

The Laplace equation (after Pierre-Simon Laplace) is the elliptic partial differential equation of second order

$\Delta \Phi =0$

for a scalar function $\Phi$ in a domain Ω $\Omega\subset\R^n$ , where Δ $\Delta$ the Laplace operator. Thus it is the homogeneous Poisson equation, that is, the right-hand side is zero. The Laplace equation is the prototype of an elliptic partial differential equation.

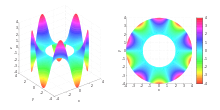
Solution of Laplace's equation on a circular ring with Dirichlet boundary values u(r=2)=0 and u(r=4)=4sin(5*θ).

Definition

The mathematical problem is to find a scalar, twofold continuously differentiable function $\Phi$ that satisfies Eq.

$\Delta \Phi =0$

is satisfied. The solutions of this differential equation $\Phi$ are called harmonic functions.

The Laplace operator Δ $\Delta$ for a scalar function is generally defined as:

$\Delta \Phi =\operatorname {div}\left(\operatorname {grad}\,\Phi \right)=\nabla ^{2}\Phi =\nabla \cdot \nabla \Phi$

Coordinate Plots

Given a particular coordinate system, one can calculate the representation of Laplace's equation in those coordinates. In the most commonly used coordinate systems, the Laplace equation can be written as:

In Cartesian coordinates

$\Delta =\sum _{{k=1}}^{n}{\frac {\partial ^{2}}{\partial x_{k}^{2}}}$ ,

from which in three-dimensional space accordingly:

${\frac {\partial ^{2}\Phi }{\partial x^{2}}}+{\frac {\partial ^{2}\Phi }{\partial y^{2}}}+{\frac {\partial ^{2}\Phi }{\partial z^{2}}}=0$

results.

In polar coordinates,

${\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}\left(\rho {\frac {\partial \Phi }{\partial \rho }}\right)+{\frac {1}{\rho ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}=0$

In cylindrical coordinates,

${\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}\left(\rho {\frac {\partial \Phi }{\partial \rho }}\right)+{\frac {1}{\rho ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial z^{2}}}=0$

In spherical coordinates,

${\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial \Phi }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\partial \Phi \over \partial \theta }\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}=0$ .

Laplace's equation

Definition

Coordinate Plots

Search by letter