Kinetic energy

Kinetic energy (from the ancient Greek κίνησις kínēsis, German 'Bewegung'), or kinetic energy, or rarely velocity energy, is the energy contained in an object due to its motion. It corresponds to the work that must be expended to move the object from rest to instantaneous motion. It depends on the mass and speed of the moving body.

The formula symbol for kinetic energy is often or $E_{\mathrm {kin} }$ . The SI unit of kinetic energy is the joule.

The concept of kinetic energy as a quantity that is conserved in elastic collisions and many other mechanical processes was introduced as vis viva ('living force') by Gottfried Wilhelm Leibniz, who, in dispute with the followers of René Descartes, saw in it the correct conservation quantity in mechanics (1686). However, this quantity was larger by a factor of 2 than the kinetic energy valid today. The factor ^1⁄2 in the formula for kinetic energy is found as early as 1726 by Daniel Bernoulli. However, the actual concept of energy did not form until the 19th century, particularly in the school of applied mathematics in France and with the advent of thermodynamics. It did not yet play a major role in 18th century mechanics, whose main object of investigation was celestial mechanics.

Kinetic energy in classical mechanics

Mass point

In classical mechanics, the kinetic energy of a mass point depends on its mass and its velocity :

$E_{{\mathrm {kin}}}={\frac {1}{2}}mv^{2}$

For example, if a car of mass traveling $m=1000\,\mathrm {kg}$ at a speed of $v=100\,\mathrm {km} /\mathrm {h}$ , it therefore has a kinetic energy of $E={\frac {1}{2}}\cdot 1000\,\mathrm {kg} \cdot \left(100\,{\frac {\mathrm {km} }{\mathrm {h} }}\right)^{2}\approx {\frac {1}{2}}\cdot 1000\,\mathrm {kg} \cdot \left(27{,}78\,{\frac {\mathrm {m} }{\mathrm {s} }}\right)^{2}=385\,800\,\mathrm {J}$ (the joule, $\mathrm{J}$ , is the SI unit of energy).

If the state of motion of the body is not described by its velocity , but by its momentum , as is usual in Hamiltonian mechanics, among other things, then the following applies to the kinetic energy (because p = m v ):

$E_{\mathrm {kin} }={\frac {p^{2}}{2m}}$

Simple derivation

If a body of mass is accelerated from rest to velocity , the acceleration work must be added for it. If the force is constant, then:

W = Fs ,

where is the distance travelled in the direction of the force. The force imparts uniform acceleration the body. , according to the basic equation of mechanics, F=ma . After a time , the velocity v=at , and the distance has been $s={\tfrac {1}{2}}at^{2}$ traveled. Putting everything in above gives the acceleration work

$W=ma\cdot {\frac {1}{2}}at^{2}={\frac {1}{2}}mv^{2}$ .

Since the kinetic energy at rest has the value zero, it reaches exactly this value after the acceleration process. Consequently, for a body of mass with velocity :

$E_{\mathrm {kin} }={\frac {1}{2}}mv^{2}$

Movement in a coordinate system

If one describes the motion of a body in a coordinate system, the kinetic energy can be calculated like this, depending on the choice of the coordinate system:

Cartesian coordinates (x, y, z):

$E_{\mathrm {kin} }={\frac {1}{2}}m\left({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}\right)$

Plane polar coordinates ( $r, \varphi$ ):

$E_{\mathrm {kin} }={\frac {1}{2}}m\left({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2}\right)$

Spherical coordinates ( $r, \varphi, \vartheta$ ):

$E_{\mathrm {kin} }={\frac {1}{2}}m\left(r^{2}\left[{\dot {\vartheta }}^{2}+{\dot {\varphi }}^{2}\sin ^{2}\vartheta \right]+{\dot {r}}^{2}\right)$

Cylinder coordinates ( $r, \varphi, z$ ):

$E_{\mathrm {kin} }={\frac {1}{2}}m\left({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2}+{\dot {z}}^{2}\right)$

Here the point above the coordinate means its change in time, the derivative with respect to time. The formulas do not take into account the energy that may be in the body's own rotation.

Rigid bodies

The kinetic energy of a rigid body with total mass and velocity $v_\mathrm{s}$ its center of gravity is the sum of the energy from the motion of the center of gravity (translational energy) and the rotational energy from the rotation about the center of gravity:

$E_{\mathrm {kin} }={\frac {1}{2}}M{v_{\mathrm {s} }}^{2}+{\frac {1}{2}}J_{\mathrm {s} }\omega ^{2}$

Here $J_\mathrm{s}$ the moment of inertia of the body with respect to its center of gravity and ω is $\omega$ the angular velocity of the rotation.

With the inertia tensor , this is generally written as:

$E_{\mathrm {kin} }={\frac {1}{2}}M{v_{\mathrm {s} }}^{2}+{\frac {1}{2}}{\boldsymbol {\omega }}^{T}I{\boldsymbol {\omega }}$

Hydrodynamics

In hydrodynamics, the kinetic energy density is often given instead of the kinetic energy. This is usually expressed by a small or : $\epsilon$

$e_{\mathrm {kin} }={\frac {E_{\mathrm {kin} }}{V}}={\frac {1}{2}}\rho v^{2}$

Here ρ $\rho$ denotes the density and V the volume.

Kinetic energy in relativistic mechanics

In relativistic physics, the above dependence of kinetic energy on velocity applies only approximately for velocities much smaller than the speed of light. From the approach that the kinetic energy $E_{\mathrm {kin} }$ the difference of total energy and rest energy follows:

$E_{\mathrm {kin} }=\gamma mc^{2}-mc^{2}=\left(\gamma -1\right)mc^{2}$

Where the speed of light, mass, and γ $\gamma$ is the Lorentz factor.

$\gamma ={\frac {1}{\sqrt {1-(v/c)^{2}}}}.$

From the Taylor expansion to v/c obtains

$E_{\mathrm {kin} }={\frac {1}{2}}mv^{2}+{\frac {3}{8}}{\frac {mv^{4}}{c^{2}}}+\cdots$ ,

so for $v\ll c$ again the Newtonian kinetic energy.

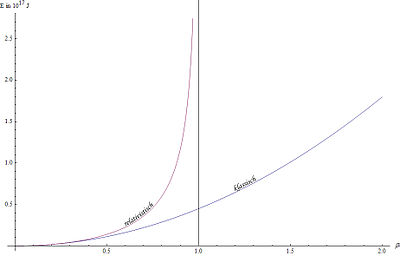
Since the energy would have to grow beyond all limits as the velocity goes toward the speed of light, $\lim _{v\to c}E_{\mathrm {kin} }=\infty ,$ it is not possible to accelerate a massed body to the speed of light.

The diagram on the right shows, for a body with mass $m = 1\, \mathrm{kg}$ , the relativistic and Newtonian kinetic energy as a function of velocity (measured in multiples of the speed of light).

Since the velocity of a moving body depends on the reference frame, this also applies to its kinetic energy. This is true in Newtonian and relativistic physics.

Application examples

→ Main article: Tests of the relativistic energy-momentum relation

In the electric field, the energy of an electron of charge and mass increases linearly with the accelerating voltage passed through. The kinetic energy is now the difference of the total relativistic energy and the rest energy ₀. The kinetic energy is thus:

$e\cdot U=E-E_{0}$

If one takes into account that for the total energy

$E^{2}=c^{2}p^{2}+E_{0}^{2}\quad (*)$

holds ( : relativistic momentum) and between momentum and total energy the relation

$cp=E\cdot {\frac {v}{c}}$

consists, it follows for the total energy from (*) thus:

$E(v)={\frac {E_{0}}{{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

Calculating the difference between E(v) and $E_{0}$ , set the expression equal to $e\cdot U$ and resolve to , we finally obtain:

$v=c\cdot {\sqrt {1-{\left({\frac {1}{1+{\frac {eU}{E_{0}}}}}\right)}^{2}}}$ with the rest energy of an electron $E_{0}=0{,}51\,{\mathrm {MeV}}$

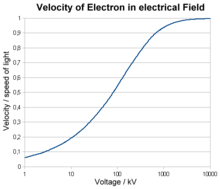
For acceleration voltages below 1 kV, the velocity can be estimated from the classical approach for the kinetic energy; at higher energies, relativistic calculations must be made. Already at a voltage of 10 kV, the electrons reach a velocity of almost 20 % of the speed of light, at 1 MV 94 %.

The Large Hadron Collider supplies protons with a kinetic energy of 6.5 TeV. This energy is about 8 thousand times greater than the rest energy of a proton. A collision between oppositely accelerated protons can produce particles with a correspondingly high rest energy.

Comparison of relativistic and classical kinetic energy

Relativistic velocity of an electron after passing through an electric field

Questions and Answers

Q: What is kinetic energy?

A: Kinetic energy is the energy possessed by an object as a result of its motion.

Q: Can kinetic energy be converted into other forms of energy?

A: Yes, kinetic energy can be converted into other forms of energy such as gravitational or electric potential energy.

Q: What is gravitational potential energy?

A: Gravitational potential energy is the energy that an object has because of its position in a gravitational field.

Q: What is electric potential energy?

A: Electric potential energy is the energy that an object has because of its position in an electric field.

Q: How is kinetic energy related to motion?

A: Kinetic energy is related to motion because its presence arises from the fact that an object is moving.

Q: Can objects possess kinetic energy when they are at rest?

A: No, objects cannot have kinetic energy when they are at rest. Kinetic energy is only present when objects are in motion.

Q: What happens to the kinetic energy of an object when it is converted into other forms of energy?

A: When kinetic energy is converted into other forms of energy, the amount of kinetic energy decreases while the amount of the new form of energy increases.