Kinematics

This article describes kinematics in the sense of classical mechanics. Kinematics as a concept of atomic, nuclear and particle physics is treated in Kinematics (Particle Processes).

Kinematics (ancient Greek κίνημα kinema, German 'Bewegung') is a field of mechanics in which the motion of bodies is described purely geometrically with the quantities time, location, velocity and acceleration. The force, the mass of the bodies and all quantities derived from them, such as momentum or energy, are not taken into account. Thus, only how a body moves is described, which is why kinematics is also called the theory of motion. Why a body moves, namely under the influence of forces, is the subject of kinetics.

Kinetics itself is a subfield of dynamics, which is classified next to kinematics in the structuring of mechanics used in the field of physics. In the structuring used in the field of engineering mechanics, kinematics and kinetics are also regarded as subfields of dynamics. Kinematics and kinetics are there together on the lowest level.

The term kinematics was coined by André-Marie Ampère in 1834.

Reference systems and coordinate systems

Reference systems form the physical framework in which a movement is described. Coordinate systems are mathematical instruments for their description; however, they are also used outside of physics. In mechanics, the solution of concrete problems always begins with the definition of a reference and coordinate system.

Reference systems

The quantities location, velocity and acceleration depend on the choice of the reference frame.

An observer at a platform perceives an arriving train as moving. For a passenger on the train, however, the train is at rest.
Observed from Earth, the Sun appears to revolve around the motionless Earth. Viewed from space, the sun is at rest and the earth is moving.

The description of motions is basically possible in all reference systems, but the description differs depending on the reference system. Planetary motion, for example, is much easier to describe with a sun at rest.

A distinction is made between systems at rest, moving and accelerated reference systems, whereby the accelerated ones are a special case of the moving reference systems. The inertial reference frames are of special importance. These are reference frames that are either at rest or moving in a straight line with constant velocity (no rotation and no acceleration), because in inertial frames Newton's first law applies: A force-free body then moves with constant velocity or remains at rest. In accelerated reference systems, on the other hand, apparent forces occur. The earth rotates around its own axis and around the sun; thus, it does not form an inertial frame. For most practical purposes, however, the Earth can be considered to be at rest to a good approximation.

Within the framework of classical mechanics, it is assumed that a location can be assigned to any body at any time. In the framework of quantum mechanics this is no longer possible. There, only residence probabilities can be given. Furthermore, in Classical Mechanics it is assumed that bodies can attain an arbitrarily high velocity and that time passes at the same rate at any location regardless of the motion. Both is not fulfilled in the relativity theory.

Coordinate systems

Coordinate systems are used for the mathematical description of reference systems. Mostly a Cartesiancoordinate system is used, which consists of axes that are perpendicular to each other. It is particularly suitable for describing rectilinear movements. For rotational motions in a plane, polar coordinates are well suited, especially if the origin is the center of the rotational motion. In three-dimensional space, cylindrical coordinates or spherical coordinates are used. If the motion of a vehicle is to be described from the driver's point of view, the accompanying tripod (natural coordinates) is used. The different coordinate systems can be converted with the coordinate transformation. A certain reference system can therefore be described by different coordinate systems.

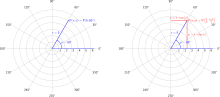
Polar coordinates

Location, velocity, acceleration and jerk

Location, velocity, and acceleration are the three central quantities of kinematics. They are related to each other through time: A change in location over time is velocity, and a change in velocity over time is acceleration. The terms velocity and acceleration refer to a straight direction at any point in time, but this direction can change constantly. For rotational motion, there is instead the angle of rotation, angular velocity, and angular acceleration. All of these quantities are vectors. They not only have a magnitude, but also a direction.

Location

For the location of a point-like body numerous notations are in use: Generally used is ${\vec {r}}$ for the location vector. This points from the coordinate origin to the point in the coordinate system at which the body is located. For Cartesian coordinates, is also common, sometimes just stands for the X component of the location vector. If the orbit of the point is known, then the location is also given by the distance traveled along the orbit. For generalized coordinates, is common. Since the location of a point changes with time , ${\vec {r}}(t),x(t),s(t)$ or also ${\vec q}(t)$ used.

The function that assigns a location to each time is the displacement-time law. In Cartesian coordinates this can be represented by the scalar functions x(t) , y(t) and , z(t) which are the components of the location vector:

$t\mapsto {\vec {r}}(t)=\left({\begin{array}{c}x(t)\\y(t)\\z(t)\end{array}}\right)=x(t)\cdot {\vec {e}}_{x}+y(t)\cdot {\vec {e}}_{y}+z(t)\cdot {\vec {e}}_{z}$

where the unit vectors $\{{\vec {e}}_{x},{\vec {e}}_{y},{\vec {e}}_{z}\}$ represent the basis (vector space) of the Cartesian coordinate system.

Speed

The change in location over time is the velocity . If the location of a body changes during a time period Δ $\Delta t$ by the distance Δ $\Delta s$ , then during this time period it has the mean velocity

$v={\frac {\Delta s}{\Delta t}}$ .

The velocity ${\vec v}(t)$ at any instant in time, the instantaneous velocity, is given by the infinitesimally small change of ${\mathrm d}{\vec r}$ the location vector during the infinitesimally small time period $\mathrm {d} t$ :

${\vec {v}}(t)=\lim _{\Delta t\to 0}{\frac {{\vec {r}}(t+\Delta t)-{\vec {r}}(t)}{\Delta t}}={\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}={\dot {\vec {r}}}(t)$ .

Thus, velocity is the derivative of location with respect to time and is denoted by a point over the location vector. In Cartesian coordinates, the velocity vector has the components $v_{x}$ , $v_{y}$ and , $v_{z}$ representing respectively the time derivative of the spatial coordinates , and

${\vec {v}}(t)=\left({\begin{array}{c}v_{x}(t)\\v_{y}(t)\\v_{z}(t)\end{array}}\right)=\left({\begin{array}{c}{\frac {\mathrm {d} x}{\mathrm {d} t}}(t)\\{\frac {\mathrm {d} y}{\mathrm {d} t}}(t)\\{\frac {\mathrm {d} z}{\mathrm {d} t}}(t)\end{array}}\right)=\left({\begin{array}{c}{\dot {x}}(t)\\{\dot {y}}(t)\\{\dot {z}}(t)\end{array}}\right)$

The velocity vector ${\vec {v}}=|{\vec {v}}|\cdot {\vec {e}}_{\parallel }$ is composed of its magnitude $|{\vec {v}}|={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}$ and the normalized direction vector ${\vec {e}}_{\parallel }$ . This direction vector thereby represents an instantaneous tangent vector to the trajectory ${\vec {r}}(t)$ the particle.

Acceleration

The change in velocity over time is the acceleration . If the velocity of a body $\Delta v$ changes $\Delta t$ by the value Δ during a time period Δ , then it has the mean acceleration

$a={\frac {\Delta v}{\Delta t}}$

The acceleration ${\vec a}(t)$ at any instant is given by the infinitesimally small change $\mathrm {d} {\vec {v}}$ of the velocity vector during the infinitesimally small period $\mathrm {d} t$ :

${\vec {a}}(t)=\lim _{\Delta t\to 0}{\frac {{\vec {v}}(t+\Delta t)-{\vec {v}}(t)}{\Delta t}}={\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}={\dot {\vec {v}}}(t)={\ddot {\vec {r}}}(t)$ .

Thus, acceleration is the first derivative of velocity with respect to time and is denoted by one point over the velocity vector, and the second derivative of location with respect to time and is denoted by two points over the location vector. In Cartesian coordinates, acceleration is given by its components $a_{x}(t)$ , $a_{y}(t)$ and $a_{z}(t)$ , which are the second time derivatives of the location components x(t) , y(t) and : z(t)

${\vec {a}}(t)=\left({\begin{array}{c}a_{x}(t)\\a_{y}(t)\\a_{z}(t)\end{array}}\right)=\left({\begin{array}{c}{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}(t)\\{\frac {\mathrm {d} ^{2}y}{\mathrm {d} t^{2}}}(t)\\{\frac {\mathrm {d} ^{2}z}{\mathrm {d} t^{2}}}(t)\end{array}}\right)=\left({\begin{array}{c}{\ddot {x}}(t)\\{\ddot {y}}(t)\\{\ddot {z}}(t)\end{array}}\right)$

The acceleration vector ${\vec {a}}={\vec {a}}_{\parallel }+{\vec {a}}_{\perp }$ can be separated into two components, which are respectively tangential and normal to the trajectory. The tangential acceleration ${\vec {a}}_{\parallel }$ describes the temporal change of the velocity amount $|\vec v|$ and forms a tangent to the trajectory curve:

${\vec {a}}_{\parallel }={\frac {\mathrm {d} |{\vec {v}}|}{\mathrm {d} t}}\cdot {\vec {e}}_{\parallel }$

The normal acceleration ${\vec {a}}_{\perp }$ , on the other hand, describes the change in velocity direction time ${\vec {e}}_{\parallel }$ and provides a measure of the curvature of the trajectory:

${\vec {a}}_{\perp }=|{\vec {v}}|\cdot {\frac {\mathrm {d} {\vec {e}}_{\parallel }}{\mathrm {d} t}}={\frac {|{\vec {v}}|^{2}}{R}}\cdot {\vec {e}}_{\perp }$

where ${\vec {e}}_{\perp }$ is a normalized normal vector of the trajectory and denotes the radius of curvature of the trajectory.

Tear

The change in acceleration over time is the jerk . If the acceleration of a point-like body changes $\Delta t$ by the value Δ a during a time period Δ $\Delta a$ , then it has the mean jerk

$j={\frac {\Delta a}{\Delta t}}$

The jerk ${\vec {j}}(t)$ at any instant results from the infinitesimally small change $\mathrm {d} {\vec {a}}$ in the acceleration vector during the infinitesimally small period $\mathrm {d} t$ :

${\vec {j}}(t)=\lim _{\Delta t\to 0}{\frac {{\vec {a}}(t+\Delta t)-{\vec {a}}(t)}{\Delta t}}={\frac {\mathrm {d} {\vec {a}}}{\mathrm {d} t}}={\dot {\vec {a}}}(t)={\ddot {\vec {v}}}(t)={\overset {...}{\vec {r}}}(t)$ .

Thus, the jerk is the first derivative of acceleration with respect to time and is denoted by two points over the velocity vector, and the third derivative of location with respect to time and is denoted by three points over the location vector. In Cartesian coordinates, the jerk is given by the components $j_{x}(t)$ , $j_{y}(t)$ and : $j_{z}(t)$

${\vec {j}}(t)=\left({\begin{array}{c}j_{x}(t)\\j_{y}(t)\\j_{z}(t)\end{array}}\right)=\left({\begin{array}{c}{\dot {a}}_{x}(t)\\{\dot {a}}_{y}(t)\\{\dot {a}}_{z}(t)\end{array}}\right)$

According to this definition, which is mainly used in physics, a uniform circular motion would be a motion with constant jerk. However, in common usage and in engineering applications, this is a jerk-free motion. The acceleration vector is therefore transformed into a body-fixed coordinate system and the derivation is performed in this system. One obtains for the jerk in the body-fixed system:

${\vec {j}}'(t)={\frac {\mathrm {d} '{\vec {a}}'}{\mathrm {d} t}}$ ,

where ${\vec {a}}'=(T_{K'}^{I})^{-1}\cdot {\vec {a}}$ and $T_{K'}^{I}$ the transformation matrix from the body fixed system to the inertial system.

In this definition, for example, the lateral pressure, which plays a major role in rail vehicles, is proportional to the change in curvature. For the alignment elements used, this is given analytically as a function of the path and can be converted into the transverse pressure for a specific speed.

Questions and Answers

Q: What is kinematics?

A: Kinematics is the branch of classical mechanics which describes the motion of points, bodies (objects) and systems of bodies (groups of objects) without looking at the cause of this motion.

Q: What does kinematic analysis measure?

A: Kinematic analysis measures the kinematic quantities used to describe motion.

Q: What are rigid transformations?

A: Rigid transformations are certain geometric transformations which are used to describe the movement of components in a mechanical system.

Q: How can kinematics be abstracted into mathematical functions?

A: It is possible to represent rotation with elements of the unit circle in the complex plane, and other planar algebras can be used to represent shear mapping in absolute time and space, as well as Lorentz transformations in relativistic space and time.

Q: How can kinematics be applied to engineering?

A: In engineering, kinematic analysis may be used to find the range of movement for a given mechanism, while working in reverse, kinematic synthesis designs a mechanism for a desired range of motion. In addition, it applies algebraic geometry to study mechanical advantage in a mechanical system or mechanism.

Q: Where else is kinematics used besides engineering?

A: Astrophysics uses it to describe celestial body movements and systems; mechanical engineering, robotics and biomechanics use it for joined parts such as an engine or robotic arm; mathematicians have developed a science using time as parameter; and it has been applied to study human skeleton motions.