Jerk (physics)

This article is about the concept of jerk in kinematics. For other meanings, see jerk (disambiguation).

Jerk is a term from kinematics. It is the instantaneous time rate of change of the acceleration of a body. The SI unit of jerk is $\mathrm {m} /\mathrm {s} ^{3}$ . As a formula symbol usually chosen, in reference to the English terms jerk or jolt.

In the development of elevator systems and gear units, the aim is to achieve values for jerk that ensure comfort and safety during operation. In the case of rail vehicles, the choice of routing elements ensures that the ride is as jerk-free as possible when passing through curves. In roller coasters, too, the load on the human body is reduced by appropriate transitions.

Formally, the jerk is the derivative of acceleration with respect to time, i.e. the second time derivative of velocity and the third time derivative of displacement:

$j(t)={\dot {a}}(t)={\ddot {v}}(t)={\overset {...}{x}}(t)$

where time, is acceleration, is velocity, and is location.

If a body-fixed coordinate system is assumed, the jerk can be determined separately for each coordinate direction, e.g. as longitudinal jerk or transverse jerk, or generally vectorially as the derivative of the acceleration with respect to this reference system. In particular, this definition ensures that a uniform circular motion is jerk-free, which corresponds to common usage, as well as application in engineering.

In impact processes, the jerk is not defined.

Although the physical quantity 'jerk' is defined for every change in acceleration, the term is generally used colloquially only for short "jerky" changes in acceleration (see web links). These occur, for example, when starting up with a tow rope that is not pretensioned. "Jerky" here means that the gradient of the kinematic jerk has a high magnitude.

Example elevator

The diagram shows for an exemplary movement of an elevator from position -6 to position +6 the relation between jerk, acceleration, velocity and displacement (the piecewise linear course of the acceleration is typical for a change of jerk (fourth derivative of the displacement after time) equal to zero):

In the first phase (0-1) the jerk is constantly greater than zero and the acceleration thus increases linearly, the velocity quadratically and the distance covered cubically.
In the second phase (1-2) the jerk is zero, the acceleration is therefore constant. The velocity changes linearly and the distance covered quadratically.
In the third phase (2-3), the jerk is constantly less than zero and the acceleration decreases linearly. The speed thus increases more and more slowly.
In the fourth phase (3-4), the jerk and also the acceleration are zero. The speed is constant and the distance covered increases linearly.
In the fifth phase (4-5), the jerk is constantly less than zero. The acceleration becomes more and more negative, thus acting as a deceleration, and the speed decreases more and more.
In the sixth phase (5-6), the jerk is zero and the acceleration is at a constant negative value. The speed decreases linearly.
In the seventh phase (6-7), the jerk has a positive value again, the negative acceleration becomes zero and the speed goes back to zero. At the end of the seventh phase, the movement comes to a standstill at position 6.

The entire time sequence is controlled so that the final position of the elevator is reached exactly. For acceleration and jerk, values are taken into account that are perceived as pleasant and comfortable.

The example could be applied in principle with other numerical values also to a moving train, which runs over a switch on a parallel track. The quantities jerk, acceleration, speed and location shown are then to be understood in the transverse direction.

However, the jerk curves shown are rather theoretical. During operation, e.g. in the case of traction elevators, oscillations can occur which cause the accelerations to be significantly greater than the nominal values.

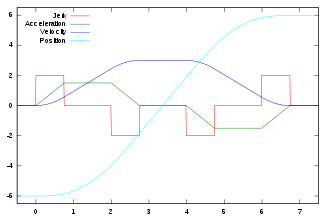
Interaction between jerk (red), acceleration (green), velocity (blue) and location (turquoise) over time. See text for explanation.

Jerk for vehicles

In vehicles, the reason for jerks is often a change in load (e.g. during partial jerking). A distinction is made between longitudinal and lateral jerk. Longitudinal jerk is the change in longitudinal acceleration over time, while lateral jerk is a change in lateral acceleration over time. This means that longitudinal jerk in a vehicle is caused by sudden starting or braking, while lateral jerk is caused by a sudden change in the steering wheel angle in a moving automobile. In the case of electronic steering systems, the additional functions can also cause jerks without actuating the steering wheel. For safety reasons, these must be limited to 5 m/s3 (ECE R79).

The designations longitudinal and transverse already indicate that these accelerations are components in a reference system fixed to the vehicle. If the components do not change, the jerk is zero. In stationary circular motion, the acceleration vector always points to the center of the circle; viewed from the outside, it therefore changes. In the vehicle-fixed coordinate system, on the other hand, the same acceleration vector remains constant.

Longitudinal pressure

The faster braking is initiated or terminated, the higher the jerk. Abruptly initiated braking (emergency braking) is associated with a high jerk. If the occupant has not adjusted quickly enough and does not brace himself, he will be thrown forward (absorbed by the seat belt in the car) when driving forward, and pressed into the seat when driving backward. Since it still takes a certain amount of time to apply the brakes even during emergency braking, the jerk remains a finite value.

If the brake remains effective at its maximum force until the vehicle comes to a standstill, a theoretically infinite jerk occurs at the end of the braking distance because the deceleration (= negative acceleration) ends suddenly, i.e. in time duration zero. As a result, the occupant is thrown into the chair by his own muscular force (supporting force) or, if he has been completely passive, by the force exerted by the belt and then thrown back by the spring force of the chair. However, time passes for these movements. This makes the jerk finite, i.e. softened. In addition, elastic elements on the vehicle (tires, wheel suspension, etc.) relax, which also takes at least some time.

In normal operation, the experienced driver releases the brake slowly before reaching standstill, thus extending the decrease in deceleration over time so that the jerk is reduced to a minimum.

Transverse pressure

The transverse jerk as a special case of the jerk is the change of the centripetal acceleration $a_{r}$ as a function of time :

$k={{\mathrm {d}}a_{{r}}(t) \over {\mathrm {d}}t}$

The centripetal acceleration of a vehicle depends on its velocity and the curvature κ $\kappa ={\tfrac {1}{r}}$ the path, where the radius of the circle of curvature:

$a_{r}={\frac {v^{2}}{r}}=v^{2}\,\kappa \Rightarrow k=v^{2}\,{\dot {\kappa }}.$

The curvature is given as a function of path length the routing elements used. With κ ${\dot {\kappa }}=v\cdot {\frac {\mathrm {d} \kappa (s)}{\mathrm {d} s}}$ thus results for the transverse pressure:

$k=v^{3}\,{\frac {\mathrm {d} \kappa (s)}{\mathrm {d} s}}.$

A transverse jerk occurs, for example, when the radius of a circular motion changes. If a circular arc immediately follows a straight line in a route, e.g. a rail track, the centripetal acceleration of rail-bound vehicles changes abruptly at this point. This means that the time for this change is almost zero and the lateral pressure becomes extremely high. If a clothoid is used as the connecting element between the straight line and the arc, the centripetal acceleration changes linearly during the time required to pass through the clothoid. Therefore, the transverse pressure is correspondingly lower.

In sections where the vehicle is moving in a straight line or at constant speed on a circular path, the centripetal acceleration does not change. The lateral pressure is therefore zero.

When planning train paths, care must be taken to ensure that the transverse pressure does not exceed a limit value of 0.4 to 0.6 m/s³, depending on the design speed and the ride comfort to be achieved for a line. In extreme cases, such as high-speed trains, the use of transition curves other than the clothoid can be used to ensure that the transverse pressure at the beginning of the transition curve does not set in abruptly but gradually.

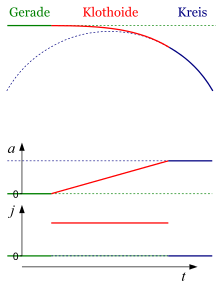
Transverse pressure and centripetal acceleration for a vehicle entering a curve at a constant speed. In the diagrams below, the time or arc length is plotted horizontally, not the horizontal vehicle position.

Jerk change

The jerk change s (jounce, snap), sometimes called bang, is a term from analytical modeling of rail vehicle vehicle dynamics and is the first derivative of jerk with respect to time.

$s(t)={\dot {j}}(t)$

where is time, is acceleration, is velocity, and location (and ). The SI unit of jerk change is accordingly ${\frac {\mathrm {m} }{\mathrm {s} ^{4}}}$ .

The change of jerk plays a theoretical role in these models, at least in the case of a piecewise continuous differentiation or integration the change of jerk is assumed to be equal to zero and in this way a solution of the corresponding equation systems is possible.

Questions and Answers

Q: What is jerk?

A: Jerk is the change in the acceleration of an object. Mathematically, it is the derivative, or rate of change of acceleration by time.

Q: What other names are used to refer to jerk?

A: Jerk is also called jolt (in British English), surge, or lurch.

Q: Is jerk a vector or scalar value?

A: Jerk is a vector and there is no word for its scalar value.

Q: How is jerk measured?

A: Jerk is measured in metres per second cubed (m/s^3).

Q: What can yank be thought as in terms of jerk?

A: Yank can be thought as a force in terms of jerk. Force is mass times acceleration and similarly, Yank is mass times jerk; it's also the derivative of the force.

Q: How does this change when an object moves near the speed of light?

A: When an object moves near the speed of light, a force may be written as the derivative of momentum instead; in this case, Yank would then be the rate of change of that derivative.