Interval arithmetic

In mathematics, interval arithmetic refers to a methodology for automated error estimation based on closed intervals. Real quantities that are not exactly known are considered, but can be delimited by two numbers and Thereby can lie between and or also take one of the two values. This range corresponds mathematically to the interval [a,b] . A function which depends on such an uncertain cannot be evaluated exactly. After all, it is not known which numerical value within [a,b] should actually be used for Instead, the smallest possible interval [c,d] determined, which just $x \in [a,b]$ contains the possible function values f(x) for all By specifically estimating the endpoints and obtains a new function, which in turn maps intervals to intervals.

Among other things, this concept is suitable for handling rounding errors directly during the calculation and if there are uncertainties in the knowledge of the exact values of physical and technical parameters. The latter often result from measurement errors and component tolerances. Furthermore, interval arithmetic can help to obtain reliable solutions of equations and optimisation problems.

As an example, we will look at the calculation of the body mass index (BMI). The BMI is the body mass in kilograms divided by the square of the height in metres. For illustration purposes, weight determination (actually mass determination) should be carried out with the help of bathroom scales, where the weight can be read off to the nearest kilogram. Thus, intermediate values are never determined - such as 79.6 kg or 80.3 kg - but figures rounded to whole numbers. Of course, it is very unlikely that you really weigh exactly 80.0 kg when this is displayed. With the usual rounding to the nearest weight value, the scale will give 80 kg for any weight between 79.5 kg and 80.5 kg. The corresponding range of all real numbers greater than or equal to 79.5 and at the same time less than or equal to 80.5 can simply be written down [79.5, 80.5] as the interval To avoid confusion, a dot is usually used as a decimal separator instead of a comma.

For a person who weighs 80 kg and is 1.80 m tall, the BMI is approximately 24.7. However, with a weight of 79.5 kg and the same height, only a value of 24.5 would have to be assumed, whereas 80.5 kg already corresponds to almost 24.9. The actual BMI is therefore in the range [24.5, 24.9] . In this case, the error can still be neglected in practice, but this is not the case for all calculations. For example, weight fluctuates during the course of a day, so that the BMI can vary between 24 (still normal weight) and 25 (already overweight). Without a detailed calculation, however, it is not always possible to say from the outset whether an error is ultimately large enough to have a significant influence.

In interval arithmetic, the range of possible results is explicitly calculated. Put simply, one no longer calculates with numbers, but with intervals that represent values that are not exactly known. Similar to an error bar around a measured value, an interval expresses the extent of uncertainty regarding the quantity to be calculated. For this purpose, simple arithmetic operations, such as the basic arithmetic operations or trigonometric functions, are redefined for calculating with intervals in order to obtain outer limits of a sought-after range of values.

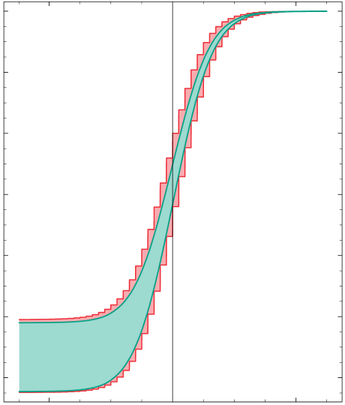
Tolerance function (turquoise) and interval approximation (red)

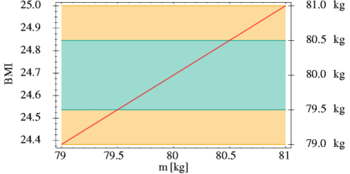
Body mass index for a 1.80 m tall person in relation to body weight m (in kilograms)

Patents

One of the major promoters of interval arithmetic, G. William Walster of Sun Microsystems, filed several patents in the field of interval arithmetic with the U.S. Patent and Trademark Office in 2003/04, partly together with Ramon E. Moore and Eldon R. Hansen. However, the validity of these claims is highly disputed in the interval arithmetic research community, as they may merely reflect prior art.

Implementations

There are many software packages that allow the development of numerical applications using interval arithmetic. These are usually implemented in the form of programme libraries. However, there are also C++ and Fortran translators that have interval data types and correspondingly suitable operations as language extensions, so that interval arithmetic is directly supported.

Since 1967, XSC extensions for scientific computation have been developed for various programming languages, including C++, Fortran and Pascal, initially at the University of Karlsruhe. The initial platform was a Zuse Z 23, for which a new interval data type with corresponding elementary operators was made available.

In 1976, Pascal-SC followed, a Pascal variant on a Zilog Z80 that made it possible to quickly create complex routines for automated result verification. This was followed by the Fortran 77-based ACRITH-XSC for the System/370 architecture, which was later also delivered by IBM. From 1991, Pascal-XSC can then be used to generate code for C compilers, and a year later the C++ class library C-XSC already supports many different computer systems. In 1997, all XSC variants were placed under the General Public License and were thus freely available. At the beginning of the 2000s, C-XSC 2.0 was redesigned under the leadership of the Working Group for Scientific Computing at the University of Wuppertal in order to better comply with the C++ standard that had been adopted in the meantime.

Another C++ class library is the Profile/BIAS ("Programmer's Runtime Optimised Fast Interval Library, Basic Interval Arithmetic") created in 1993 at the TU Hamburg-Harburg, which provides the usual interval operations in a user-friendly way. Special emphasis was placed on efficient utilisation of the hardware, portability and independence from a special interval representation.

The Boost collection of C++ libraries also contains a template class for intervals. Its authors are currently trying to get interval arithmetic included in the C++ language standard.

Today, the common computer algebra systems, such as Mathematica, Maple and MuPAD, can also handle intervals. There is also the extension INTLAB for Matlab, which builds on BLAS routines, as well as the toolbox b4m, which provides a profile/BIAS interface.

IEEE Standard 1788-2015

An IEEE standard for interval arithmetic was published in June 2015. There are two free reference implementations developed by members of the working group: The libieeep1788 library for C++ and the interval package for GNU Octave.

A simplified version of the standard is still being developed. This should be even easier to implement and ensure faster dissemination.

Conferences and workshops

Several international conferences and workshops are held annually around the world. The most important conference is SCAN (International Symposium on Scientific Computing, Computer Arithmetic, and Verified Numerical Computation). There are also SWIM (Small Workshop on Interval Methods), PPAM (International Conference on Parallel Processing and Applied Mathematics) and REC (International Workshop on Reliable Engineering Computing).