Integer

Integer is a redirect to this article. For the representation of integer values in digital computers, see Integer (data type).

The integers (also integers, lat. numeri integri) are an extension of the natural numbers.

The integers include all numbers

…, −3, −2, −1, 0, 1, 2, 3, …

and thus contain all natural numbers $\mathbb {N} _{0}$ and their additive inverses. The set of integers is usually denoted by the double-stroke letter $\mathbb {Z}$ (the "Z" stands for the German word "Zahlen"). The alternative symbol ${\mathbf {Z}}$ is now less common; one disadvantage of this boldface symbol is that it is difficult to display by handwriting. The Unicode of the character is U+2124 and has the shape ℤ.

The above enumeration of the integers also simultaneously gives their natural order in ascending order. Number theory is the branch of mathematics that deals with properties of the integers.

The representation of integers in the computer is usually done by the data type integer.

Integers are typically introduced in math classes in fifth through seventh grade.

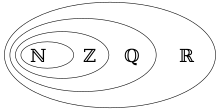
The integers (ℤ) are part of the rational numbers (ℚ), which in turn are part of the real numbers (ℝ). They themselves contain the natural numbers (ℕ).

Properties

Ring

The integers form a ring with respect to addition and multiplication, i.e. they can be added, subtracted and multiplied without restriction. Calculation rules such as the commutative law and the associative law for addition and multiplication apply, and the distributive laws also apply.

The existence of subtraction allows linear equations of the form

a + x = b

with natural numbers and can always be solved: x = b - a . If one restricts to the set of natural numbers, then not every such equation is solvable.

In abstract terms, this means the integers form a commutative unitary ring. The neutral element of addition is 0, the additive inverse element of is , the neutral element of multiplication is 1.

Arrangement

The set of integers is totally ordered, in the order

. $\cdots < -2 < -1 < 0 < 1 < 2 < \cdots$

That is, you can compare two integers each. One speaks of

positive $\{1,2,3,\ldots \}$	$[=\mathbb {N} ]$ ,		non-negative $\{0,1,2,3,\ldots \}$	$[=\mathbb {N} _{0}]$ ,
negative $\{\ldots ,-2,-1\}$	$[=-\mathbb {N} ]$ and		non-positive $\{\ldots ,-2,-1,0\}$	$[=-\mathbb {N} _{0}]$

integers. The number 0 itself is neither positive nor negative. This order is compatible with the arithmetic operations, ie:

If a<b and $c \leq d$ , then a + c < b + d .

If a<b and 0 < c , then ac < bc .

With the help of the arrangement, the sign function

$\operatorname {sgn}(x):={\begin{cases}-1&{\text{falls }}\quad x<0\\~~\,0&{\text{falls }}\quad x=0\\~~\,1&{\text{falls }}\quad x>0\end{cases}}$

and the magnitude function

$|x|=\operatorname {abs} (x):={\begin{cases}~~\,x&{\text{falls }}\quad x\geq 0\\-x&{\text{falls }}\quad x<0\end{cases}}$

define. They hang as follows

$x=\operatorname {sgn}(x)\,|x|$

together.

Thickness

Like the set of natural numbers, the set of integers is also countable.

The integers do not form a body because, for example, the equation is 2x = 1 not solvable in $\mathbb {Z}$ . The smallest body containing $\mathbb {Z}$ is the rational numbers $\mathbb {Q}$ .

Euclidean ring

An important property of the integers is the existence of division with remainder. Because of this property, two integers always have a greatest common divisor, which can be determined using the Euclidean algorithm. In mathematics, is called $\mathbb {Z}$ a Euclidean ring. From this also follows the theorem of unique prime factorization in $\mathbb {Z}$ .

Construction from the natural numbers

If the set of natural numbers is given, then the integers can be constructed from it as an extension of the number range:

On the set $\N_0 \times \N_0$ of all pairs of natural numbers, the following equivalence relation is defined:

$(a, b) \sim (c, d)$ , if a + d = c + b

Addition and multiplication on $\mathbb {N} _{0}\times \mathbb {N} _{0}$ is defined by:

$\begin{align} (a, b) + (c, d) &= (a + c, b + d)\\ (a, b) \cdot (c, d) &= (ac + bd, ad + bc) \end{align}$

$\mathbb {Z} =\mathbb {N} _{0}\times \mathbb {N} _{0}\,/\!\sim$ is now the set of all equivalence classes.

The addition and multiplication of the pairs now induce well-defined links on $\mathbb {Z}$ , with which $\mathbb {Z}$ becomes a ring.

The usual order of the integers is defined as

(a, b) < (c, d) if a + d < c + b .

Each equivalence class (a, b) has, in the case $a\geq b$ , a unique representative of the form (n,0) , where n=a-b , and in the case a unique a<b representative of the form (0,n) , where n=b-a .

The natural numbers can be embedded in the ring of integers by mapping the natural number to the equivalence class represented by (n,0) Usually, the natural numbers are (n,0) identified with their images and the equivalence (0,n) class represented by denoted by

If is a natural number different $0$ from , the equivalence class represented by (n,0) called a positive integer and the equivalence class represented by (0,n) called a negative integer.

This construction of the integers from the natural numbers works even if instead of $\mathbb {N} _{0}$ the set $\mathbb {N}$ , that is, without $0$ , is taken as the initial set. Then the natural number is in the equivalence class of (n+1,1) and the is $0$ in that of (1,1) .