Injective function

This article is about injective mappings. For injective moduli and other injective objects, see Injective object.

Injectivity or link uniqueness is a property of a mathematical relation, i.e. in particular also of a function (for which one usually also says "mapping" equivalently): An injective function, also called injection, is a special case of a left-unique relation, namely the one in which the relation is also right-unique and left-total.

A function $f\colon X\to Y$ is injective if for every element the target set is at most one (i.e. possibly no) element the initial or definition set aims at it, i.e. if never two or more different elements of the definition set are mapped to the same element of the target set:

$f(x_1)=f(x_2) \Rightarrow x_1=x_2$

The target set can therefore not be less powerful than the definition set, i.e. it cannot contain fewer elements.

The image set $f(X):=\{f(x)\mid x\in X\}$ may be a true subset of the target set , i.e., there may be elements $y\in Y$ not image elements f(x) as is the case in the graph shown on the right. This is the difference to a bijective mapping, which in addition to injectivity requires that every element of the target set f(x) occurs as a picture element i.e. that is surjective.

That a mapping $f\colon X\to Y$ is injective is occasionally by $f\colon X\hookrightarrow Y$ , with a $\to$ sign composed of ⊂ $\subset$ → It is reminiscent of the embedding of a set in a superset by a function $f\colon X\to Y,\, f(x)=x,$ which maps each element of to itself.

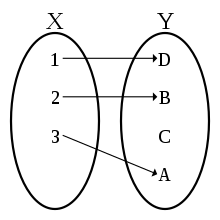
Illustration of an injection. Each element of Y has at most one original image: A, B, D one each, C none.

Examples and counterexamples

Extra-mathematical example: The function that assigns the number of the current identity card to each citizen of the Federal Republic of Germany with an identity card is injective, where the set of all possible identity card numbers is assumed as the target set (because identity card numbers are only assigned once).
$\mathbb {N}$ denote the set of natural numbers and $\mathbb {Z}$ the set of integers.

$f_1\colon \N \to \N,\, x \mapsto 2x$ is injective.

$f_2\colon \Z \to \Z,\, x \mapsto 2x$ is injective.

$f_3\colon \N \to \N,\, x \mapsto x^2$ is injective.

$f_4\colon \Z \to \Z,\, x \mapsto x^2$ is not injective, since, for example, f(1)=f(-1) holds.

Any function $f\colon X \to Y,\, x \mapsto f(x)$ from a two-element set $X=\{a,b\}$ into a one-element set $Y=\{c\}$ is not injective, because necessarily both elements of $c\in Y$ are mapped to the single element

f(a)=f(b)=c despite $a\neq b$

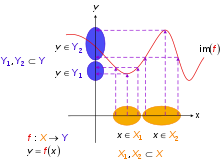
Non-injective function

Properties

Note that the injectivity of a function depends $f\colon A\to B$ only on the function graph $\{(x, f(x)) \mid x \in A\}$ (unlike surjectivity, which also depends on the target set read from the function graph).
function $f\colon A\to B$ is injective exactly if for all subsets $X, Y \subseteq A$ holds: $f(X \cap Y)=f(X) \cap f(Y)$
function $f\colon A\to B$ is injective if and only if $f^{-1}(f(T))=T$ for all $T \subseteq A$ (where denotes $f^{-1}\colon {\mathcal {P}}(B)\to {\mathcal {P}}(A)$ the primal image function).
If the functions $f\colon A\to B$ and $g\colon B\to C$ are injective, then the composition (concatenation) is also $g \circ f\colon A \to C$ injective.
From the injectivity of $g\circ f$ it follows that is injective.
function $f\colon A\to B$ with non-empty definition set is injective if and only if a left inverse, that is a function $g\colon B \to A$ with $g \circ f = \operatorname{id}_A$ (where denotes $\operatorname {id} _{A}$ the identical mapping to ).
function $f\colon A\to B$ is injective if it is left truncable, i.e. if for any function $g, h\colon C \to A$ $f \circ g = f \circ h$ the equality follows from (This property motivates the term monomorphism used in category theory, but for general morphisms injective and left truncable are no longer equivalent).
Any function $f\colon A\to B$ is $f=h\circ g$ representable as a concatenation , where surjective and injective (namely an inclusion mapping).
A continuous real-valued function on a real interval is injective if it is strictly monotonically increasing or strictly monotonically decreasing in its entire domain of definition, i.e. if for any two numbers and from the domain of definition the applies: From f ( a (increasing), or from f ( a (falling).

A group or vector space homomorphism is injective exactly when its kernel is trivial, i.e. consists only of the neutral element or the zero vector.

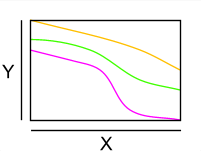
Three injective strictly monotonically decreasing real functions.

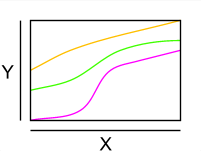
Three injective strictly monotonically increasing real functions.

Mightiness of sets

The notion of injection plays an important role in set theory in the definition and comparison of powers, a notion that generalises the number of elements from finite sets to arbitrary sets. Two sets $X,\,Y$ are called "of equal power" if there is both an injection from to and one from to (In this case, bijections from one set to the other also exist). On the other hand, is called of smaller power than if there is an injection from to but none from to .

Drawer closure

A frequent inference scheme in proofs, especially in number theory, uses the statement that a mapping a finite set into a set with fewer elements cannot be injective, that there are elements $a,b\in X$ with $a\neq b$ and equal image f(a)=f(b) Because of the notion of many objects in fewer drawers, this is called "drawer closure".

Number of injective mappings

The number of injective mappings from a defining set into a given finite target set with property $|B| \geq |A|$ is given by:

$|B|\cdot (|B|-1) \cdot \ldots \cdot (|B|-|A|+1) = \frac{|B|!}{(|B|-|A|)!} = |A|! \cdot \binom{|B|}{|A|}$

In combinatorics, this corresponds to a variation without repetition.

Questions and Answers

Q: What is an injective function in mathematics?

A: An injective function is a function f: A → B with the property that distinct elements in the domain map to distinct elements in the codomain.

Q: What is the relation between elements in the domain and codomain of an injective function?

A: For every element b in the codomain B, there is at most one element a in the domain A such that f(a)=b.

Q: Who introduced the terms injection, surjection, and bijection?

A: Nicholas Bourbaki and a group of other mathematicians introduced the terms injection, surjection, and bijection.

Q: What does an injective function mean?

A: An injective function means that each element in the domain A maps to a unique element in the codomain B.

Q: How is an injective function different from a 1-1 correspondence?

A: An injective function is often called a 1-1 (one-to-one) function but is distinguished from a 1-1 correspondence, which is a bijective function (both injective and surjective).

Q: What is the property of an injective function?

A: The property of an injective function is that distinct elements in the domain map to distinct elements in the codomain.

Q: What is the significance of injective functions in mathematics?

A: Injective functions play an important role in many mathematical fields, including topology, analysis, and algebra, due to their property of having distinct elements in the domain map to distinct elements in the codomain.