Inflection point

The title of this article is ambiguous. For other meanings, see Turning point (disambiguation).

In mathematics, an inflection point is a point on a function graph at which the graph changes its curvature behavior: The graph changes here either from a right-hand curve to a left-hand curve or vice versa. This change is also called an arc change. The determination of inflection points is part of a curve discussion.

An inflection point $W\left(x_{W}|f(x_{W})\right)$ at the inflection point $\ x_{W}$ exists if the curvature of the function graph $x_{W}$ changes its sign at the point From this, several sufficient criteria for determining inflection points can be derived. One criterion requires that the second derivative of the differentiable function changes sign at the point $\ x_{W}$ Other criteria require only that the second derivative of the function be zero and that certain higher derivatives be nonzero.

If one considers the second derivative of a function as "slope of its gradient", its inflection points can also be interpreted as [local] extrema, i.e. [local] maxima or minima, of its gradient.

Tangents through a turning point (drawn in red in the picture) are called turning tangents. Turning points where these turning tangents run horizontally are called saddle, terrace or horizontal turning points.

Analogous to the term extreme value, the term inflection value for the corresponding function value seems $f(x_{W})$ intuitively plausible and is also used by some sources. However, it is pointed out directly or indirectly (by using quotation marks, for example) that this tends to be an unusual term.

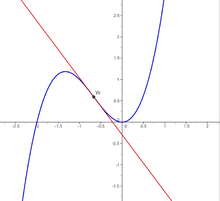
Turning point with turning tangent

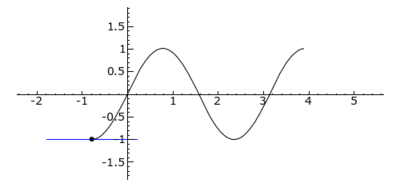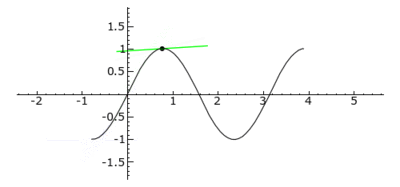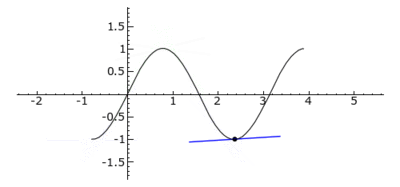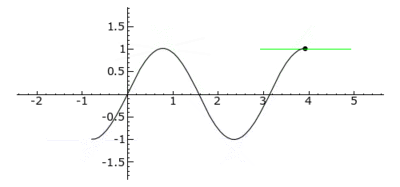
Curvature behavior of the function sin(2x). The tangent is colored blue in convex areas, green in concave areas and red at inflection points.

Definition

Let be ${]a,b[}\subset \mathbb{R}$ an open interval and is a $f\colon {]a,b[}\to \mathbb {R}$ continuous function. We say has an inflection point in $x_{0}$ if there are intervals $]\alpha ,x_{0}[$ and $]x_{0},\beta [$ that either.

is $]\alpha ,x_{0}[$ convex in and $]x_{0},\beta [$ concave in or that
is $]\alpha ,x_{0}[$ concave in and $]x_{0},\beta [$ convex in

This means that the graph of the function changes the sign of its curvature at the point $x_{0}$ The curvature of a twice continuously differentiable function is described by its second derivative.

Criteria for determining inflection points

In the following we assume that the function $f\colon {]a,b[}\to \mathbb {R}$ is differentiable sufficiently often. If this is not true, the following criteria are not applicable in the search for inflection points. First, a necessary criterion is presented, that is, any twice continuously differentiable function must $x_{W}$ satisfy this criterion at some point so that under some circumstances there is an inflection point at that point. Then some sufficient criteria are given. If these criteria are fulfilled, then there is certainly an inflection point, however, there are also inflection points which do not fulfill these sufficient criteria.

Necessary criterion

Let $f\colon {]a,b[}\to \mathbb {R}$ is a twice continuously differentiable function, then, as already noted in the definition, the second derivative describes the curvature of the function graph. Since an inflection point is a point at which the sign of the curvature changes, the second derivative of the function must be zero at this point. Thus, it holds:

If $x_{W}$ an inflection point, then $f\,''(x_{W})=0$ .

Sufficient criterion without using the third derivative

In curve discussions, one of the following two sufficient conditions is usually used. In the first condition, only the second derivative occurs; for this, the sign of $f\,''(x)$ must be $x>x_{W}$ $x<x_{W}$ for x > x

$\left.{\begin{array}{ll}f{\text{ ist in einer Umgebung von }}x_{W}{\text{ zweimal differenzierbar.}}\\f\,''(x){\text{ wechselt an der Stelle }}x_{W}{\text{ das Vorzeichen.}}\end{array}}\right\}\Rightarrow x_{W}{\text{ ist Wendestelle.}}$

If $\,f''(x_{W})$ changes from negative to positive, then is right-to-left turning point. If $x_{W}$ $\,f''(x_{W})$ changes from positive to negative at $x_{W}$ $x_{W}$ a left-right turning point.

Sufficient criterion using the third derivative

In the second condition sufficient for a turning point, the third derivative is also needed, but only at the point $x_{W}$ itself. This condition is mainly used when the third derivative can be easily determined. The main disadvantage compared to the already explained condition is that in case $f\,'''(x_{W})=0$ no decision can be made.

$\left.{\begin{array}{ll}f{\text{ ist in einer Umgebung von }}x_{W}{\text{ dreimal differenzierbar.}}\\f\,''(x_{W})=0\\f\,'''(x_{W})\neq 0\end{array}}\right\}\Rightarrow x_{W}{\text{ ist Wendestelle.}}$

More precisely, it follows from $f\,''(x_{W})=0$ and $f\,'''(x_{W})>0$ , that at $x_{W}$ has a minimum of slope, i.e., a right-to-left turning point, while conversely for $f\,''(x_{W})=0$ and $f\,'''(x_{W})<0$ x W $x_{W}$ has a maximum of the slope, i.e. a left-right turning point.

Sufficient criterion using further derivations

If the function is differentiable sufficiently often, a decision can also be made in the case $f\,'''(x_{W})=0$ This is based on the evolution of at the point $x_{0}$ using Taylor's formula:

$\left.{\begin{array}{ll}f{\text{ ist in einer Umgebung von }}x_{W}\,n{\text{-mal differenzierbar.}}\\f\,''(x_{W})=\ldots =f\,^{{(n-1)}}(x_{W})=0\\f\,^{{(n)}}(x_{W})\neq 0\;{\text{ mit }}\,n>2\,{\text{und}}\,n\,{\text{ungerade}}\end{array}}\right\}\Rightarrow x_{W}{\text{ ist Wendestelle.}}$

This more general formulation contains with it already the preceding case: Beginning with the third derivative the next derivative different from zero is looked for, and if this is a derivative of odd order, it is a turning point.

Or formulated in general terms: If the first nonzero derivative $f^{(n)}$ of the function at the point $x_{0}$ where $f''(x_{0})=0$ a derivative of odd order > 2, f {\displaystyle has an inflection point at this point.

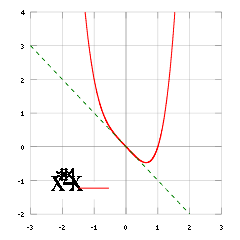
For the function f(x)=x4-x, the second derivative at x=0 is zero; but (0,0) is not an inflection point because the third derivative is also zero and the fourth derivative is nonzero.

Example

${f(x)}={1 \over 3}\cdot x^{3}-2\cdot x^{2}+3\cdot x$

Then the second derivative of the function is given by:

${f''(x)}={2\cdot x-4}$

A turning point $x_{W}$ must satisfy the condition

{f''(x)}=0 resp.

${2\cdot x-4}=0$

satisfy. From this follows $x_{W}=2$ . In order to clarify whether there is actually a turning point at this point, we now also examine the third derivative:

${f'''(x)}=2\,$

From $f\,'''(x_{W})=f'''(2)=2\neq 0$ concluded that this is a turning point. This fact can be seen even without using the third derivative: Because of $f\,''(x)=2\cdot x-4<0$ < 2 x<2 x ) for x $f\,''(x)=2\cdot x-4>0$ > the curvature behavior x>2 ; therefore, there must be a turning point.

The coordinate of this inflection point is obtained by substituting x=2 into the function equation.

$y_{W}=f(2)={1 \over 3}\cdot 2^{3}-2\cdot 2^{2}+3\cdot 2={2 \over 3}$

The equation of the tangent of inflection can be determined by substituting the x-coordinate of the inflection point (2) into the first derivative. Thus one receives the gradient (m). Afterwards one puts into the function determination (y = mx + b) the determined x & y coordinate of the turning point and the m (gradient) value. Then you get the intersection with the y-axis (b) and thus the complete equation of the tangent of inflection.

$f\,'(x)=x^{2}-4\cdot x+3$

$f\,'(2)=2^{2}-4\cdot 2+3=-1$

Angle tangent: $y=-x+{8 \over 3}$

Special cases

The graph of the function $f(x)=(x-2)\cdot e^{{|x|}}$ changes x=0 its curvature behavior at (transition from right to left curvature). The first derivative at the point x=0 does not exist, so the above formalism is not applicable. Nevertheless, the function has an inflection point at x=0

The graph of the function with the equation $f(x)=x^{2}$ in the positive domain and $f(x)=-x^{2}$ in the negative domain and at x=0 , i.e., f(x)=x|x| , has a first but no second derivative at the point $0$ but nevertheless there is a point of inflection.