Logical disjunction

The title of this article is ambiguous. For other meanings, see Disjunction (disambiguation).

OR is a redirect to this article. For other meanings, see Oder (disambiguation).

Disjunction ("or-connection", from lat. disiungere "to separate, to distinguish, not to mix") and adjunction (from lat. adiungere, "to attach, to connect") are in logic the terms for two types of statements, where two propositions are connected by an excluding or or by a non-excluding or:

  1. The non-exclusive disjunction (alternative, adjunction, inclusive or, OR) "A or B (or both)" states that at least one of the two statements involved is true. Thus, it is false only if both A and B are false.
  2. The exclusionary disjunction (contravalence, exclusive or, XOR) "(either) A or B (but not both)" states that exactly one of the two statements involved is true (if the disjunction is true). The exclusionary disjunction is therefore false if either both statements involved are false or if both statements involved are true. Excluding disjunction is also called contravalence and is discussed in more detail under this heading.
  3. Only occasionally the non-exclusive disjunction of the negations of the statements involved is also called disjunction of A and of B, that is the statement "not A or not B (or both)" respectively equivalently "not (A and B)". This conjunction is called, among other things, Sheffer's line, NAND, or exclusion (in the sense of logic). It corresponds to the set-theoretic notion of disjoint.

Less frequently used terms for disjunction are alternative, contrajunction, bisubtraction and alternation. The ambiguous use of "disjunction" etc. is traceable to the different roles of the natural-linguistic or. The partial statements of a disjunction (adjunction) are called disjuncts (adjuncts), and the word ("or") linking the partial statements is called a disjunct (adjunct).

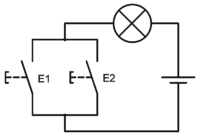
Technical realization of the non-exclusive disjunction in the OR gate: If pushbutton E1 or E2 is pressed, the lamp lights up. This logical OR also includes the case where both are pressed at the same time.Zoom
Technical realization of the non-exclusive disjunction in the OR gate: If pushbutton E1 or E2 is pressed, the lamp lights up. This logical OR also includes the case where both are pressed at the same time.

Zoom

Venn diagram of {\displaystyle A\lor B}
The union of sets is defined via (non-exclusive) disjunction.

Non-exclusive disjunction

The non-exclusive disjunction (alternative, adjunction) is a compound statement of the type "A or B (or both)"; it states that at least one of the two statements involved is true.

Notation

{\displaystyle A\lor B}

In Polish notation, the capital letter A is used for disjunction:

Aab

In the notation {\displaystyle A\lor B}of a conjunction of statements, the symbol \lor (Unicode: U+2228, ∨) stands for the non-exclusive disjunction as a propositional junction. It resembles the character \textstyle \cupfor the unification set, and is reminiscent of the letter "v" that begins the Latin word "vel", which stands for such a non-exclusive Or.

The truth table for the vel function (OR function of a gate) as a truth value function of the non-exclusive disjunction is thus:

A

B

{\displaystyle A\lor B}

true

true

true

true

Incorrect

true

Incorrect

true

true

Incorrect

Incorrect

Incorrect

A disjunction is a Boolean expression, it is associative and commutative.

It follows from what has been said:

  • If A is false and if B is false, the disjunction is false; in every other case it is true.
  • If the disjunction is false, then both A and B are false.
  • If the disjunction is true, one of the following must be true:
    1. both disjoints are true
    2. A is false and B is true or
    3. A is true and B is false

Example

The statement "Tom helps paint or Anna helps paint" consists of the following parts:

  • the partial statement/disjunct A: "Tom helps paint".
  • the disjunctive "or", here not understood as exclusive
  • the partial statement/disjunct B: "Anna helps paint".

Neither partial statement here excludes the other. The statement is false if neither Tom nor Anna help paint, true otherwise. In particular, it is also true if both Tom and Anna help paint.

Excluding disjunction

→ Main article: Contravalence

The exclusionary disjunction (contravalence, XOR) is a compound statement in which two statements are linked with the phrase "either - or (but not both)", for example the statement "Anna is either studying French or she is studying Spanish (but not both)." This excludes the case where both sub-statements are true - in the example, the case where Anna studies both French and Spanish - this is precisely the difference between this and non-exclusive disjunction. The Latin expression for the exclusionary or is "aut - aut".

The truth table for the aut-function (XOR-function of a gate) as a truth value function of the exclusionary disjunction is thus:

A

B

{\displaystyle A~{\dot {\lor }}~B}

true

true

Incorrect

true

Incorrect

true

Incorrect

true

true

Incorrect

Incorrect

Incorrect

AlegsaOnline.com - 2020 / 2023 - License CC3