Improper rotation
A rotation reflection is a congruence mapping of the three-dimensional Euclidean space in itself. It is composed of a rotation and a reflection on a plane that is intersected at right angles by the axis of rotation. A related figure is the rotation inversion, which consists of a rotation and a reflection at a point on the axis of rotation. In both cases, the order of the rotation and reflection sub-operations is irrelevant in execution. Rotational mirroring and rotational inversion give the same result if (i) the centre of inversion is the point of intersection of the mirror plane with the axis of rotation and (ii) the two angles of rotation differ by π 
The rotation angles 0° and 180° provide particularly easy results:
- A rotation mirroring by 0° (= rotation inversion by 180°) is a simple plane mirroring: The point P of the adjacent figure is projected vertically downwards along the blue line.
- A rotational reflection by 180° (= rotational inversion by 0°) is a point reflection at the intersection of the mirror plane with the axis of rotation (in the illustration the red point in the blue plane): The point P is thus projected obliquely backwards and downwards along the red line.
Since it is actually a point reflection, the result in this case does not depend on the position of the axis as long as it passes through the inversion centre.
If the origin of a Cartesian coordinate system is placed in the inversion centre, a rotation reflection is represented by an orthogonal matrix 


an. In a rotational inversion the matrix has the same form, only φ must be replaced 
The repeated application of a rotation reflection with angle φ 





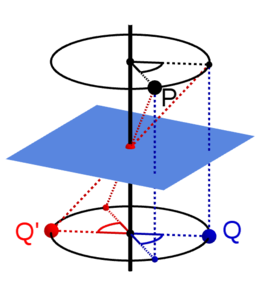
If the point P is first rotated around the black axis of rotation and then mirrored at the blue plane (or vice versa), the projection is onto the point Q. If, on the other hand, it is mirrored at the inversion centre (red point in the blue plane) after the rotation (or vice versa), the projection is onto point Q'.
Search within the encyclopedia

