Hypercube

This article is about the dimensional polytope hypercube; for the communication pattern, see hypercube (communication pattern).

Hypercubes or dimensional polytopes are -dimensional analogues of the square ( n=2 ) and the cube ( n=3 ). Here can be any natural number. The four-dimensional hypercube is also called a tesseract. The symmetry group of a hypercube is the hyperoctahedral group.

Projection of a tesseract (four-dimensional hypercube) into the 2nd dimension

Regular cube construction

Regular cubes of edge length $a\neq 0$ can be generated as follows:

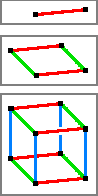
If a point is moved in a straight line by the distance a , the result is a one-dimensional line, mathematically a one-dimensional hypercube.
If this distance is shifted perpendicular to its dimension by the distance , the result is a two-dimensional square, a surface, mathematically a two-dimensional hypercube.
If this square is shifted perpendicular to its two dimensions by the distance , the result is a three-dimensional cube, mathematically equivalent to a three-dimensional hypercube.
General: Thus, if an -dimensional cube is shifted perpendicular to its dimensions by distance , a -dimensional hypercube is formed.

Boundary Elements

In a hypercube of dimension there are exactly edges at each vertex. Accordingly, a hypercube is an undirected multigraph (see also: graph theory).

The -dimensional cube is bounded by zero-dimensional, one-dimensional, ..., $(n\!-\!1)$ -dimensional elements. By example:

The 3-dimensional cube is bounded by nodes (points), edges (lines) and faces, i.e. by elements of the dimensions 0,1 and 2.

The number of individual boundary elements can be derived from the following consideration: Let be $n\!+\!1$ given a hypercube of dimension The -dimensional boundary elements of this cube ( $k_{{n+1}}$ ) can be generated from the boundary elements of an -dimensional hypercube as follows: the -dimensional boundary elements ( $k_{{n}}$ ) double and all $k\!-\!1$ dimensional elements $(k\!-\!1)_{n}$ are expanded to -dimensional ones. Thus, the sum gives a number of $k_{{n+1}}=2k_{{n}}+(k-1)_{{n}}$ .

Example

The 2-dimensional hypercube is bounded by 1 face $(k_{{n}}=2)$ , 4 edges $(k_{{n}}=1)$ and 4 nodes $(k_{{n}}=0)$ .

The 3-dimensional cube is bounded by faces $(k_{{n+1}}=2)$ , bounded by edges $(k_{{n+1}}=1)$ and Nodes $(k_{{n+1}}=0)$ .

Another way to think about it is: If one places an -dimensional hypercube in a Cartesian coordinate system centered about the origin and aligned along the coordinate axes, there are to a -dimensional boundary element there are coordinate axes that are parallel to that boundary element. On the other hand, for each choice of coordinate axes, there is not only one -dimensional boundary element, but $2^{n-k},$ because by each of the n-k axes perpendicular to the boundary elements, one doubles the number of boundary elements (there are the same boundary elements again parallel-shifted on the other side of the axis). Thus, the number of boundary elements is the product of the number of ways axes to select from the axes with the number of boundary elements for each selection, and is thus ${\binom {n}{k}}\cdot 2^{n-k}$ (with the binomial coefficient ${\binom {n}{k}}$ ).

Schläfli symbol

Number of boundary elements

0-dim.

1-dim.

2-dim.

3-dim.

4-dim.

$\ldots$

$(n\!-\!1)$ -dim.

-dim.

Item

Route

$\{\}$

Square

$\{4\}$

3-dim. cube

$\{4,3\}$

4-dim. cube

$\{4,3,3\}$

$\vdots$

-dim.
cube

$\{4,3^{n-2}\}$

$2^{n}$

$n2^{{n-1}}$

${\binom {n}{2}}2^{n-2}$

${\binom {n}{3}}2^{n-3}$

$\ldots$

${\binom {n}{n-1}}2^{1}=2n$

${\binom {n}{n}}2^{0}=1$

Each -dimensional boundary element of an -dimensional cube of edge length is, for $0<k\leq n$ , a -dimensional cube of the same edge length . Thus a 4-hypercube has 16 vertices, an edge mesh of length $32a$ , is bounded by a surface mesh of total area $24a^{2}$ and by cells with total 3 volume (the 3-dimensional hypersurface) of $8a^{3}$ and has a 4 volume of $a^{4}$ .

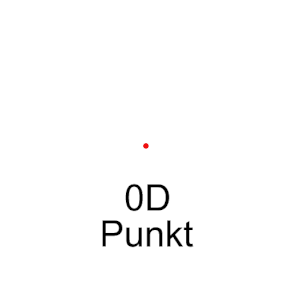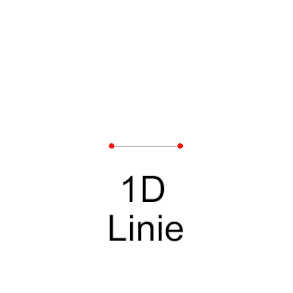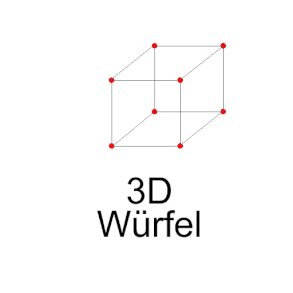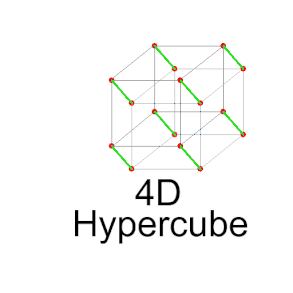
The way to the hypercube

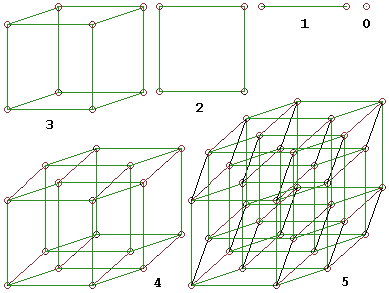
The 0- to 5-dimensional cubes in parallel projection

Questions and Answers

Q: What is a hypercube?

A: A hypercube is an n-dimensional analogue of a square (n = 2) and a cube (n = 3). It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.

Q: What is the longest diagonal in an n-dimensional hypercube?

A: The longest diagonal in an n-dimensional hypercube is equal to n {\displaystyle {\sqrt {n}}}.

Q: Is there another term for an n-dimensional hypercube?

A: An n-dimensional hypercube is also called an n-cube or an n-dimensional cube. The term "measure polytope" was also used but it has now been superseded.

Q: What does "unit hypercube" mean?

A: A unit hypercube is a hypercube whose side has length one unit. Often, the unit hypercube refers to the specific case where all corners have coordinates equal to 0 or 1.

Q: How can we define a "hyperrectangle"?

A: A hyperrectangle (also called an n-orthotope) is defined as the general case of a hypercube.