Hyperbola

In plane geometry, a hyperbola is a special curve consisting of two symmetrical branches extending to infinity. Along with the circle, the parabola and the ellipse, it is one of the conic sections that result from the intersection of a plane with a straight circular cone.

Like ellipse and parabola, hyperbolas can be defined as locus curves in the plane (see section Definition of a hyperbola as locus curve).

Any hyperbola can be $\;{\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1\;$ described in a suitable coordinate system by the equation (see section Equation).

The hyperbola was discovered by Menaichmos. The name, introduced by Apollonios of Perge, comes from Greek and refers to hyperbole (ὑπερβολή hyperbolé, from ancient Greek βάλλειν bállein, German 'werfen', ὑπερβάλλειν hyperballein, German 'to throw beyond the target') of the intersection angle (or numerical eccentricity ε $\varepsilon$ , see below) in the conic section: as the intersection angle increases, the circle ( $\varepsilon=0$ ) turns first into increasingly elongated ellipses and then, via the parabola ( $\varepsilon =1$ and the intersecting plane is parallel to a tangent plane of the cone) into hyperbolas with ε

Hyperbola with center , foci $F_{1}$ and $F_{2}$ , vertices $S_{1}$ and $S_{2}$ , asymptotes (green)

Definition of a hyperbola as a locus

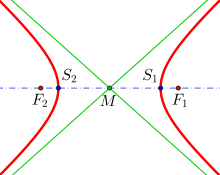
A hyperbola is defined as the set of all points the drawing plane E^2 , for which the magnitude of the difference of the distances to two given points, called foci $F_{1}$ and $F_{2}$ , is constant equal to

$H = \{P \in E^2 \mid ||PF_2| - |PF_1 || = 2a \}$

The center of the foci is called the center of the hyperbola. The connecting line of the foci is the major axis of the hyperbola. On the major axis lie the two vertices S_1,S_2 at distance from the center. The distance of the foci from the center is called focal length or linear eccentricity and is usually denoted by The dimensionless numerical eccentricity ε mentioned in the introduction $\varepsilon$ is $\tfrac e a$ .

That the intersection of a straight circular cone with a plane steeper than the cone's generatrices and not containing the cone's apex is a hyperbola is shown by proving the above defining property using Dandelin's spheres (see section Hyperbola as a conic section).

Remark:
The equation ||PF_2| - |PF_1 || = 2a can also be interpreted like this: If is $c_{2}$ the circle around $F_{2}$ with radius , then has the $c_{2}$ same distance from the circle as from the focal point $F_{1}$ : $|Pc_{2}|=|PF_{1}|\ .$ One calls $c_{2}$ the leading circle of the hyperbola belonging to $F_{2}$ It generates the right branch

$H_{+}=\{P\in E^{2}\mid |Pc_{2}|=|PF_{1}|\}$

of the hyperbola. The left branch $H_{-}$ obtained analogously with the guide circle belonging to $F_{1}$ the focal point $c_{1}$ .
The generation of a hyperbola with guide circles should not be confused with the generation of a hyperbola with guide lines (see below).

Due to the guiding circle property, a branch of a hyperbola is the equidistance curve to one of its foci and the guiding circle with the other focus as center.

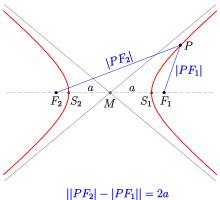
Hyperbola: definition and asymptotes

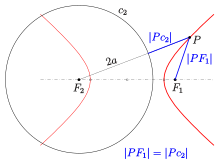
Hyperbola: definition with guide circle

Hyperbola in 1st main layer

Equation

The equation of the hyperbola obtains a particularly simple form if it is in 1st principal position, that is, if the two foci lie on the axis symmetrically with respect to the origin; thus, for a hyperbola in 1st principal position, the foci have the coordinates (e, 0) and (-e, 0) (with e = linear eccentricity), and the vertices have coordinates (a, 0) and (-a, 0) .

For any point (x,y) in the plane, the distance to the focal point equal to (e,0) $\sqrt{ (x-e)^2 + y^2 }$ and to the other focal point $\sqrt{ (x+e)^2 + y^2 }$ . Thus the point (x,y) lies on the hyperbola exactly when the difference of these two expressions is equal to or equal to -2a

By algebraic transformations and using the abbreviation b^2 = e^2-a^2 we can show that the equation

$\sqrt{(x-e)^2 + y^2} - \sqrt{(x+e)^2 + y^2} = \pm 2a$

to the equation

$\frac{x^2}{a^2}-\frac{y^2}{b^2}= 1$

is equivalent. The latter equation is called the equation of the hyperbola in 1st principal position.

Vertex

A hyperbola has only two vertices: (a,0) and (-a,0) . In contrast to the ellipse, (0,b) and (0,-b) not curve points. The latter are therefore also called imaginary minor vertices. The straight line through the minor vertices is called minor axis. The hyperbola is symmetrical to the major and minor axis.

Asymptotes

If we solve the hyperbolic equation for , we get

$y=\pm b\sqrt{\frac{x^2}{a^2}-1}.$

Here you can see that the hyperbola for magnitude large straight lines

$y=\pm \frac{b}{a}x$

arbitrarily close. These straight lines pass through the center and are called the asymptotes of the hyperbola $\tfrac{x^2}{a^2}-\tfrac{y^2}{b^2}= 1.$

Half parameter p

The half length of a hyperbolic chord passing through a focal point and perpendicular to the principal axis is called the half parameter (sometimes also transverse dimension or just parameter) of the hyperbola. It can be calculated by

$p = \frac{b^2}a.$

Other meaning of :

is the vertex radius of curvature,

i.e., is the radius of that circle through a vertex which best fits the hyperbola at the vertex. (See below: collection of formulas/vertex equation.)

Tangent

The equation of the tangent line at a hyperbolic point most easily found by (x_B,y_B) implicitly differentiating the hyperbolic equation $\tfrac{x^2}{a^2}-\tfrac{y^2}{b^2}= 1$ :

$\frac{2x}{a^2}-\frac{2yy'}{b^2}= 0 \ \rightarrow \ y'=\frac{x}{y}\frac{b^2}{a^2}\ \rightarrow \ y=\frac{x_B}{y_B}\frac{b^2}{a^2}(x-x_B) +y_B.$

Considering $\tfrac{x_B^2}{a^2}-\tfrac{y_B^2}{b^2}= 1$ get:

$\frac{x_B}{a^2}x-\frac{y_B}{b^2}y = 1.$

Equilateral hyperbola

A hyperbola for which a=b holds is called an equilateral hyperbola. Its asymptotes are perpendicular to each other. The linear eccentricity is $e=\sqrt{2}a$ , the numerical eccentricity ε $\varepsilon=\sqrt{2}$ and the half parameter is p=a .

Parameter representation with hyperbolic functions

With the hyperbolic functions $\cosh,\sinh$ get a parameter representation (analogous to the ellipse) of the hyperbola $\tfrac{x^2}{a^2}-\tfrac{y^2}{b^2}= 1$ :

$(\pm a \cosh t, b \sinh t),\, t \in \R$

Hyperbola in 2nd main layer

If we swap and we get hyperbolas in 2nd principal position:

$\frac{y^2}{a^2}-\frac{x^2}{b^2}= 1$

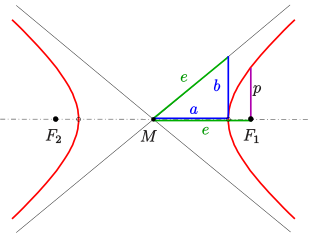
Hyperbola: semiaxes a,b, lin. eccentricity e, half parameter p

Questions and Answers

Q: What is a hyperbola?

A: A hyperbola is a type of conic section, which is a curve formed by the intersection of a cone and a plane. It is created when the plane intersects both halves of a double cone, creating two curves that look exactly like each other but open in opposite directions.

Q: How does one create a hyperbola?

A: A hyperbola is created when the plane intersects both halves of a double cone, creating two curves that look exactly like each other but open in opposite directions. This occurs when the angle between the axis of the cone and the plane is less than the angle between a line on the side of the cone and the plane.

Q: Where can we find examples of hyperbolas in nature?

A: Hyperbolas can be found in many places in nature. For example, an object in open orbit around another object - where it never returns - can move in the shape of a hyperbola. On a sundial, the path followed by the tip of the shadow over time is also shaped as a hyperbola.

Q: What equation describes one well-known example of a hyperbola?

A: One well-known example of an equation describing anhyperbola is f(x)=1/x .

Q: What are some other types of conic sections besides hyperbolae?

A: Other types of conic sections include parabolas, ellipses, and circles.

Q: How do these different types differ from each other?

A: Parabolas are U-shaped curves with one vertex point; ellipses are oval shapes with two focal points; circles have no vertex points or focal points; and finally,hyperbolae have two separate curved lines opening outwards from their center point at different angles.