Angular diameter

This article or subsequent section is not sufficiently supported by evidence (e.g., anecdotal evidence). Information without sufficient evidence may be removed in the near future. Please help Wikipedia by researching the information and adding good supporting evidence.

This article deals with the geometrical term. For the astronomical concept of brightness, see Apparent brightness.

The apparent size (also apparent diameter) of an object arises in visual perception from the angle at which the direct or reflected light radiation emanating from it falls into the eye. The terms visual angle and visual angle are sometimes used synonymously; in astronomy, among other fields, one also speaks of angular extent. The visual angle determines the size of the image of the object in the eye. Objects of the same dimensions appear different sizes at different distances because they are imaged on the retina at different angles of vision. The adjustment of the lens is called accommodation.

To artificially increase the angle of vision, one uses optical devices such as magnifying glasses, light microscopes, telescopes, binoculars and telescopes.

How the viewer interprets the apparent size depends, among other things, on his perception of space, see relative size.

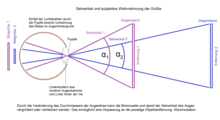
Subjective perception of size as a function of the angle of vision

Dimension and apparent size

The figure opposite illustrates the relationship between the apparent size α, distance r (viewing distance) and true extent g of an object. The following relationship can be derived between the three quantities:

$\tan {\frac {\alpha }{2}}={\frac {{\frac {g}{2}}}{r}}$ and thus for angle α $\alpha =2\,\arctan \left({\frac {g}{2\,r}}\right)$

In geodesy, the distance can be calculated from the apparent size by means of an object of standardized size, for example a vertically erected lath:

$r = \frac{g}{2\, \tan\tfrac{\alpha}{2}}$

In astronomy, if the distance of an object is known, its approximate true extent transverse to the line of sight is given by

$g = 2\,r\,\tan\frac{\alpha}{2}$

For small angles < 1°, the small angle approximation applies, in radians: $\textstyle x\approx \tan x\approx \sin x$ , so that in angular minutes:

$\alpha \approx \frac{10800 \cdot g}{\pi \cdot r}$ .

The error is only 0.4" (1.7-10-6 rad or 0.001%) for α=1°, and only 0.004" (2-10-9 rad or 0.0001%) for α=6'=0.1°.

For a spherical object whose diameter is g and the distance to the center of the sphere is r, the deviating formula α $\textstyle \alpha =2\arcsin({\frac {g}{2\,r}})$ , because in the triangle the right angle is not at the midpoint, but at the point of tangency. The difference disappears for small angles.

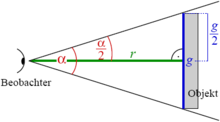
Apparent size

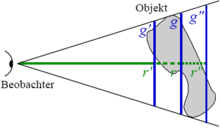
Differences in the calculated expansions g, g′ and g″ of an irregular object depending on the given distances r, r′ and r″.

Vertical and horizontal angle of view

In photography, the vertical and horizontal angles of view of an object are used. The vertical visual angle εv of an object is defined by circumscribing a horizontal rectangle around the object fixed by the eye, then drawing the two rays emanating from the eye to the end points of the vertical line through the center of the rectangle and determining the angle between these rays. Similarly, the horizontal visual angle εh is the angle between the two rays from the eye to the endpoints of the horizontal line through the center of the rectangle.

If one chooses the Cartesian coordinate system whose origin lies in the center of the rectangle, whose y- and z-axis form the vertical and horizontal symmetry axis of the rectangle and where the observer is located in the half-space x > 0, then these two viewing angles can be determined trigonometrically for the rectangle with the vertical side length Gv = 2γv and the horizontal side length _Gh = 2γh for any observer point (x,y,z):

$\epsilon_v = \arctan\frac{\gamma_v-y}{\sqrt{ x^2 + z^2 }} - \arctan\frac{-\gamma_v-y}{\sqrt{ x^2 + z^2 }}$ ,

$\epsilon_h = \arctan\frac{\gamma_h-z}{\sqrt{ x^2 + y^2 }} - \arctan\frac{-\gamma_h-z}{\sqrt{ x^2 + y^2 }}$ .

Due to the rotational symmetry of the function graph of the vertical visual angle εv(x,y,z) when rotating around the y-axis (cylindrical symmetry), its investigation can be restricted to the x,y-plane. For the visual angle functions as functions of the plane coordinates x and y only, the following terms and the function graphs shown in the figures are obtained:

$\epsilon_v = \arctan\frac{\gamma_v-y}{x} - \arctan\frac{-\gamma_v-y}x$ ,

$\epsilon_h = 2\, \arctan\frac{\gamma_h}{\sqrt{ x^2 + y^2 }}$

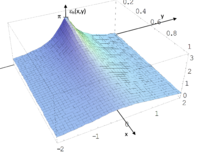
Graph of the horizontal angle of view

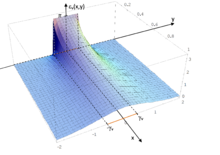
Graph of the vertical angle of vision

vertical and horizontal viewing angle

Angular diameter

Dimension and apparent size

Vertical and horizontal angle of view

Search by letter