Angular momentum

The angular momentum (in mechanics also spin or, in antiquated form, momentum or momentum momentum, in quantum mechanics in some cases also spin) is a physical conservation quantity. For example, a system has angular momentum when it rotates around its centre of mass, such as a spinning top, an athlete performing a pirouette or a planetary system.

The angular momentum is a vectorial quantity, namely a pseudo-vector. Its dimension is the product of mass, length and velocity. This is equal to the product of energy and time and thus also the dimension of the quantity effect. In the SI system of units, it is measured in joule seconds ( $\mathrm {Js}$ ). Its formula symbol is ${\vec {L}}$ or ${\vec {J}}$ .

The angular momentum of a system is the sum of the angular momentum of its components. The angular momentum of a component of the system is generally made up of two components (see #The angular momentum of a rigid body):

the orbital angular momentum, as the fraction that arises due to a movement of a body with mass with respect to a reference point, provided the body does not move directly towards or away from the reference point.
the intrinsic angular momentum, as the portion that is not orbital angular momentum. In mechanics, this part is caused by the rotation around the centre of mass of the body. In quantum mechanics, it is the spin.

The angular momentum always refers to the point in space that is chosen as the reference point of the rotational movement. In a freely rotating system, the centre of gravity is often set as the reference point, in astronomy usually the centre of gravity of the central star. If the rotation is given by a bearing, a point on the axis is usually chosen.

The angular momentum can generally be calculated as the vector product of the position vector ${\vec {r}}$ and the momentum ${\vec {p}}$ the body:

${\vec {L}}={\vec {r}}\times {\vec {p}},$

or with the aid of the inertia tensor $\mathbf {\Theta }$ and the angular velocity ω {\displaystyle $\omega$

${\vec {L}}=\mathbf {\Theta } \cdot {\vec {\omega }}.$

In quantum mechanics, angular momentum is described by the angular momentum operator. This shows that it is a quantised quantity. The amount of angular momentum is always an integer or half-integer multiple of Planck's reduced quantum of action. The direction of the angular momentum is also quantised. It is subject to directional quantisation with respect to the quantisation axis. The role of the intrinsic angular momentum is performed by the spin, which is not associated with spatial motion. Thus, the angular momentum operator is composed of the components orbital angular momentum operator ${\hat {\mathbf {L} }}={\hat {\mathbf {r} }}\times {\hat {\mathbf {p} }}$ and spin operator.

Leonhard Euler introduced the law of angular momentum in 1775 as a fundamental principle in mechanics that is independent of Newton's laws. It states that a torque must act on the system to change the angular momentum. The conservation of angular momentum can be experienced in many places in everyday life (see video, or pirouette effect).

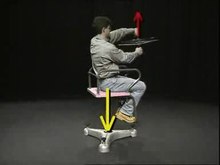
Play media file Demonstration experiment on conservation of angular momentum (video, 18 s). When the person applies a torque, the angular momentum of the wheel changes its direction to vertical (red arrow). According to the principle of actio equals reactio, the reaction torque gives the swivel chair an opposite angular momentum (yellow arrow). The vertical angular momentum of zero remains the same.

Definition and illustration

For a mass point moving at location ${\vec {r}}$ with momentum ${\vec {p}}=m{\vec {v}}$ the angular momentum is given by the cross product

$\vec{L} = \vec{r}\times\vec{p}$

is defined. The reference point is the origin ${\vec {r}}=0$ . For the angular momentum around another reference point one has to ${\vec {r}}_{0}$ ${\vec {r}}'=({\vec {r}}-{\vec {r}}_{0})$ replace ${\vec {r}}$ by

A suitable illustration is the case where the mass point performs a plane circular motion around the origin. Then the angular momentum vector is perpendicular to the circular plane, i.e. in the direction of the axis of the circular motion, and has the magnitude

$L=mrv=mr^{2}\omega$ .

The angular momentum increases with

higher angular velocity ω $\omega$ proportional,
greater mass also proportional,
greater distance this mass to the axis of rotation, however, in a quadratic ratio.

The angular momentum vector points in the direction in which a right-hand screw would move forward with the same direction of rotation. The corkscrew rule or right-fist rule applies: If the curved fingers of the right hand indicate the direction of the rotary motion, the thumb points in the direction of the angular momentum (see picture). The fact that the right hand must be used for this rule and not the left is due to the definition of the cross product of two vectors.

The angular momentum of an extended body to a certain reference point is obtained by forming the angular momentum of its mass points to this reference point and adding them vectorially.

Even if the designation suggests otherwise, even those bodies have an angular momentum that, from a visual point of view, do not perform any rotation at all. Even a body moving in a straight line and not rotating around itself has angular momentum if the reference point is chosen so that it is not on the path of the centre of mass of the body. The angular momentum is then simply calculated from the product of mass, velocity and the perpendicular distance of the reference point from the path. Therefore, reference systems can always be found in which no angular momentum belongs to the movement of the centre of mass. The angular momentum of a body rotating around its centre of mass, on the other hand, only disappears in a co-rotating, i.e. accelerated, reference frame.

With the right-hand rule, the direction of the angular momentum vector can be determined as the direction of the thumb.

Conservation of angular momentum

Experience shows that the angular momentum of an isolated physical system remains unchanged in terms of magnitude and direction, regardless of the internal forces and interactions between the components of the system. This is called conservation of angular momentum. Almost perfectly isolated systems are, for example, the atomic nuclei, the molecules in dilute gases and astronomical objects in space. Kepler's second law, according to which a planet moves faster in its eccentric orbit the closer it is to the sun, can be derived from the conservation of angular momentum.

The conservation of angular momentum also applies in the presence of external forces if these forces as a whole do not exert a torque on the system. In a homogeneous gravitational field, this applies, for example, to the angular momentum of each body around its own centre of gravity. If the external forces on different parts of a system are parallel to each other, the component of the angular momentum parallel to the forces is preserved in any case.

Conservation of angular momentum can be seen, for example, in toy spinning tops, discus throwing and the pirouette effect.

The conservation of angular momentum applies to any physical system (e.g. also electromagnetic fields) and can be derived with the help of Noether's theorem from the fact that the physical laws do not depend on the orientation of the system under consideration in space.

Displacement, rotation, reflection

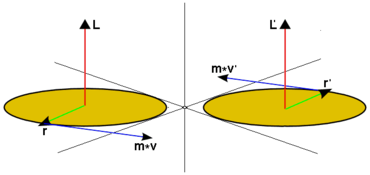
The amount and direction of the angular momentum of a point mass depend on which point one chooses as the reference point. When the reference point is moved, the vector of each location changes to ${\vec {x}}^{\,\prime }={\vec {x}}+{\vec {a}}$ and the angular momentum changes to

${\vec {L}}^{\prime }={\vec {L}}+{\vec {a}}\times {\vec {p}}.$

Often the centre of mass or a point that is at rest during the considered rotations, i.e. lies on the axis of rotation, is chosen as the reference point.

The cross product of two vectors is always perpendicular to the plane spanned by them, but a rotation of the system under consideration rotates both the position vectors and the orbital velocities by the same amount, whereby the angular momentum is also rotated in the same way.

In a point reflection at the reference point, the location changes to the opposite location. The sign of the velocity in relation to this point also reverses. When forming the cross product, these two changes of sign compensate each other, so that the angular momentum does not change in a point reflection. This distinguishes it from the behaviour of the velocity or the position vector: the angular momentum belongs to the class of pseudovectors.

While position vector ${\vec {r}}$ and momentum ${\vec {p}}=m{\vec {v}}$ reverse their direction in a point reflection around the coordinate origin, that of the angular momentum remains ${\vec {L}}=m{\vec {r}}\times {\vec {v}}$ unchanged with respect to the centre of the disk (In the picture the vectors are drawn in bold and not with arrow).

Euler's angular momentum theorem

→ Main article: Twist set

In order to change the momentum of a body, a force must act. More precisely, the change in momentum over time is the force:

${\frac {\mathrm {d} {\vec {p}}}{\mathrm {d} t}}={\vec {F}}.$

Quite analogously, in 1754 Leonhard Euler formulated Euler's angular momentum theorem, according to which the change in angular momentum over time with respect to the origin is equal to the applied torque ${\vec {M}}$ about the origin:

${\frac {\mathrm {d} {\vec {L}}}{\mathrm {d} t}}={\vec {M}}.$

To change the angular momentum of a body, a torque must occur. A torque is the cross product of distance vector ${\vec {r}}$ and force ${\vec {F}}$ :

${\vec {M}}={\vec {r}}\times {\vec {F}}.$

The angular momentum theorem is obtained by deriving the angular momentum with respect to time, for example, for a point mass at location ${\vec {x}}$ :

${\frac {\mathrm {d} {\vec {L}}}{\mathrm {d} t}}={\dot {\vec {L}}}={\frac {\mathrm {d} }{\mathrm {d} t}}[{\vec {x}}\times {\vec {p}}]={\underline {{\dot {\vec {x}}}\times {\vec {p}}}}+{\vec {x}}\times {\dot {\vec {p}}}={\vec {x}}\times {\vec {F}}={\vec {M}}.$

Since the velocity and momentum are parallel, their cross product in the underlined term is omitted. In order to change the (orbital) angular momentum of a point mass, a momentum which ${\vec {M}}$ ${\vec {F}}$ corresponds to the moment of the force acting on the point mass. In the case of an extended body, a pair of forces with resulting force ${\vec {F}}={\vec {0}}$ also able to trigger a change in angular momentum, which concerns the intrinsic angular momentum, see below. Of course, the intrinsic angular momentum does not apply to a point mass.

If the force is a central force ${\vec {F}}=f{\tfrac {\vec {x}}{|{\vec {x}}|}}$ , the angular momentum about the centre is preserved, because the change in angular momentum over time - the attacking moment of the central force - disappears:

${\frac {\mathrm {d} {\vec {L}}}{\mathrm {d} t}}={\vec {x}}\times \left(f{\frac {\vec {x}}{|{\vec {x}}|}}\right)={\frac {f}{|{\vec {x}}|}}\underbrace {{\vec {x}}\times {\vec {x}}} _{={\vec {0}}}={\vec {0}}.$

Consequently, the angular momentum around the centre is constant over time. This applies in particular to planetary movements around a central star.

Plane path, area theorem

If the angular momentum of a point mass (for example, the Earth orbiting the Sun) maintains its initial value at all times, then the orbit of the point mass is in a plane.

For the cross product is perpendicular to its factors and at all times applies to the angular momentum with respect to the origin of the coordinates

${\vec {x}}(t)\cdot {\vec {L}}(t)={\vec {x}}(t)\cdot {\bigl (}{\vec {x}}(t)\times m{\vec {v}}(t){\bigr )}=0,$

if is the mass and ${\vec {v}}$ is the orbital velocity of the point mass. If now the angular momentum is time-independent, ${\vec {L}}(t)={\vec {L}}(0),$ then each orbital point satisfies the plane equation

${\vec {x}}(t)\cdot {\vec {L}}(0)=0.$

It is therefore a movement in the plane through the centre of mass of the system perpendicular to the angular momentum.

Then Kepler's second law (also called the area theorem) applies: The driving beam to the planet sweeps over equal areas in equal times.

For in a short time ${\mathrm {d}}t$ the driving beam ${\vec {x}}$ changes by ${\vec {v}}\mathrm {d} t$ and sweeps the area of the triangle with these two sides. The triangle is half the size of the parallelogram spanned by the two vectors, whose content is given by the magnitude of the cross product. In the time ${\mathrm {d}}t$ the driving beam therefore sweeps the area

$\mathrm {d} F={\frac {1}{2}}\left|{\vec {x}}(t)\times {\vec {v}}(t)\,\right|\,\mathrm {d} t={\frac {1}{2\,m}}{\bigl |}{\vec {L}}{\bigr |}\mathrm {d} t.$

If the angular momentum does not change with time, the surface velocity is therefore constant. This fact can also be generalised to situations in which the angular momentum changes, see Twist Theorem#Surface Theorem.

The area theorem also applies in relativistic physics if, in addition, the energy conserved. For in relativistic physics

${\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} t}}={\frac {\vec {p}}{E}}\,c^{2}$

and

$\mathrm {d} F={\frac {c^{2}}{2\,E}}{\bigl |}{\vec {L}}{\bigr |}\mathrm {d} t.$

For plane orbits there is a relation between angular momentum ${\vec {L}}$ and angular velocity ω ${\vec {\omega }}$ which is relevant for the Runge-Lenz vector:

${\vec {L}}=mr^{2}{\vec {\omega }}.$

To prove this, one decomposes the velocity into a radial and an azimuthal component (see polar coordinates/velocity), ${\dot {\vec {r}}}={\dot {r}}{\vec {e}}_{r}+r{\dot {\varphi }}{\vec {e}}_{\varphi }$ . In the cross product with the radial velocity is ${\vec {r}}=r{\vec {e}}_{r}$ dropped and one obtains

${\vec {L}}={\vec {r}}\times m{\dot {\vec {r}}}=mr^{2}{\dot {\varphi }}\,{\vec {e}}_{r}\times {\vec {e}}_{\varphi }=mr^{2}{\dot {\varphi }}{\vec {e}}_{z}=mr^{2}{\vec {\omega }}.$

The angular momentum of a rigid body

The angular momentum of a body is the sum of the angular momentum of its components:

${\vec {L}}=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {x}}}_{n}$

or for a body with continuous mass distribution the integral:

${\vec {L}}=\int \mathrm {d} ^{3}x\,\rho ({\vec {x}})\,{\vec {x}}\times {{\vec {v}}({\vec {x}})}$

$m_{1\ldots N}$ ... the masses of the mass points of the body with discrete mass distribution
$\rho ({\vec {x}})$ ... the mass density of the continuous mass distribution
${\vec {x}}_{1\ldots N}$ and ${\dot {\vec {x}}}_{1\ldots N}$ ... the locations and velocities of the mass points of the body with discrete mass distribution.
${\vec {v}}({\vec {x}})$ ... the velocity field indicating the speed at which the mass is moving at location ${\vec {x}}$

With the help of the centre of mass of a body and its position coordinate ${\vec {s}}$ as well as its centre of gravity velocity ${\dot {\vec {s}}}$ position coordinates related to it can be calculated χ ${\vec {\chi }}:={\vec {x}}-{\vec {s}}$ and the angular velocities of the mass points ω ${\vec {\omega }}_{n}$ be defined. Then the velocities can be expressed as:

${\begin{aligned}{\dot {\vec {x}}}_{n}&={\dot {\vec {s}}}+{\vec {\omega }}_{n}\times {\vec {\chi }}_{n}\\{{\vec {v}}({\vec {x}}})&={\dot {\vec {s}}}+{\vec {\omega }}_{n}\times {\vec {\chi }}.\end{aligned}}$

Moreover, for a rigid body whose orientation to the reference point is constant, all angular velocities are equal $(\forall n:{\vec {\omega }}_{n}\equiv {\vec {\omega }})$ . This gives the angular momentum to:

${\begin{aligned}{\vec {L}}&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times \left({\dot {\vec {s}}}+{\vec {\omega }}\times {\vec {\chi }}_{n}\right)\\&=M{\vec {s}}\times {\dot {\vec {s}}}+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right){\text{ bzw.}}\\{\vec {L}}&=\int \mathrm {d} ^{3}x\,\rho ({\vec {x}})\,{\vec {x}}\times \left({\dot {\vec {s}}}+{\vec {\omega }}\times {\vec {\chi }}\right)\\&=M{\vec {s}}\times {\dot {\vec {s}}}+\int \mathrm {d} ^{3}\chi \rho ({\vec {\chi }})\,{\vec {\chi }}\times \left({\vec {\omega }}\times {\vec {\chi }}\right){\text{ oder verallgemeinert}}\\&=M{\vec {s}}\times {\dot {\vec {s}}}+\mathbf {\Theta } _{s}\cdot {\vec {\omega }}.\end{aligned}}$

Here are additional

$M=\sum _{n}m_{n}$ the total mass of the body and
$\mathbf {\Theta } _{s}=\int \mathrm {d} ^{3}x\rho ({\vec {x}})\,[({\vec {x}}\cdot {\vec {x}})\,\mathbf {1} -{\vec {x}}\otimes {\vec {x}}]$ the inertia tensor of the body with respect to its centre of mass.

Derivation

Derivation

The derivation uses various conversions, the Graßmann identity (BAC-CAB formula), and the definition of the centre of mass:

${\begin{array}{lllll}{\vec {L}}&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times \left({\dot {\vec {s}}}+{\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&&\left|{\text{Ausklammern}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {x}}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&\left|+{\vec {0}}={\vec {s}}-{\vec {s}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,\left({\vec {x}}_{n}-{\vec {s}}+{\vec {s}}\right)\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&\left|{\text{Ausklammern}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,\left({\vec {x}}_{n}-{\vec {s}}\right)\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+\sum _{n}m_{n}\,{\vec {s}}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&\left|{\vec {x}}_{n}-{\vec {s}}={\vec {\chi }}_{n}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+\sum _{n}m_{n}\,{\vec {s}}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&\left|{\text{Graßmann-Identität}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+\sum _{n}m_{n}\,\left({\vec {\omega }}\left({\vec {s}}\cdot {\vec {\chi }}_{n}\right)-{\vec {\chi }}_{n}\left({\vec {s}}\cdot {\vec {\omega }}\right)\right)&\left|{\text{Summe in die Klammer}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+{\vec {\omega }}\left({\vec {s}}\cdot \sum _{n}m_{n}{\vec {\chi }}_{n}\right)-\sum _{n}m_{n}{\vec {\chi }}_{n}\left({\vec {s}}\cdot {\vec {\omega }}\right)&\left|\sum _{n}m_{n}\chi _{n}={\vec {0}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+0\\&=M{\vec {s}}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&\left|{\text{Graßmann-Identität}}\right.\\&=M{\vec {s}}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\omega }}\left({\vec {\chi }}_{n}{\vec {\chi }}_{n}\right)-{\vec {\chi }}_{n}\left({\vec {\omega }}{\vec {\chi }}_{n}\right)&&\left|{\text{Dyadisches Produkt}}\otimes \right.\\&=M{\vec {s}}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,\left(({\vec {\chi }}_{n}{\vec {\chi }}_{n})\mathbf {1} -{\vec {\chi }}_{n}\otimes {\vec {\chi }}_{n}\right){\vec {\omega }}\end{array}}$

The first term $M{\vec {s}}\times {\dot {\vec {s}}}$ is called orbital angular momentum, the second term is the intrinsic angular momentum.

The inherent angular momentum

→ Main article: Inertia tensor

The intrinsic angular momentum of a rigid body is the fraction of its angular momentum that ${\vec {s}}$ can be represented by the rotation about its centre of mass With the help of the angular velocity ω ${\vec {\omega }}_{s}$ and the inertia tensor $\mathbf {\Theta } _{s}$ , each related to ${\vec {s}}$ the centre of mass , it can be calculated as their matrix product:

${\vec {L}}_{s}=\mathbf {\Theta } _{s}\cdot {\vec {\omega }}_{s}.$

In general, ω ${\vec {\omega }}$ and ${\vec {L}}_{s}$ not point in the same direction - a rotating body will "yaw" if it is free to move, or show unbalance if the direction of the axis is fixed. Only when rotating about one of the body's principal axes of inertia are ω ${\vec {\omega }}$ and ${\vec {L}}_{s}$ parallel, so that conservation of angular momentum also causes the direction of the axis of rotation to remain constant, and hence the moment of inertia to remain constant. The inertia tensor is symmetrical and therefore the principal axes of inertia are orthogonal in pairs. From the inertia tensor, one can calculate the moment of inertia and the principal axes of inertia for any axis of rotation by solving the eigenvalue problem.

Angular momentum in relativity theory

In relativity theory, angular momentum cannot be embedded in a four-vector. This is already obvious from the fact that $L_{i}=\varepsilon _{ijk}x_{j}p_{k}$ under Lorentz transformations like $L'_{i}=\varepsilon _{ijk}\Lambda ^{\mu j}x_{\mu }\Lambda ^{\nu k}p_{\nu }$ transformed. This problem is circumvented by $M^{\mu \nu }$ introducing the angular momentum tensor This is defined as

$M_{\mu \nu }=x_{\mu }p_{\nu }-p_{\mu }x_{\nu }$

and its entries are

$\left(M_{\mu \nu }\right)={\begin{pmatrix}0&-N_{x}&-N_{y}&-N_{z}\\N_{x}&0&L_{z}&-L_{y}\\N_{y}&-L_{z}&0&L_{x}\\N_{z}&L_{y}&-L_{x}&0\end{pmatrix}}$

with $N_{i}=\gamma mcx_{i}-cp_{i}t.$

Questions and Answers

Q: What is angular momentum?

A: Angular momentum, also known as rotational momentum, is the product of an object's moment of inertia and its angular velocity.

Q: How is angular momentum calculated?

A: Angular momentum is calculated by multiplying an object's moment of inertia and its angular velocity. This can be expressed mathematically as L = Iω, where I is the moment of inertia (the resistance to angular acceleration or deceleration) and ω is the angular velocity.

Q: What are the three kinds of angular momentum?

A: The three kinds of angular momentum are vibrational, spin, and orbital.