Angular frequency

The angular frequency or angular frequency is a physical quantity of the vibration theory. The formula symbol is the Greek letter ω $\omega$ (small omega) is used. It is a measure of how fast an oscillation proceeds. Unlike the frequency , however, it does not indicate the number of oscillation periods related to a time span, but the swept phase angle of the oscillation per time span. Since one period of oscillation corresponds to $2\pi$ a phase angle of , the angular frequency differs from the frequency by a factor of $2\pi$ :

$\omega =2\pi f={\frac {2\pi }{T}}$ ,

where is the period of the oscillation. The unit of angular frequency is $1/\mathrm {s}$ . Unlike frequency, this unit is not called a hertz for angular frequency.

Radians for angles: The angle that cuts out of the circumference the length of the radius of the circle is 1 radian. So the solid angle is $2\pi$ radians.

Pointer model

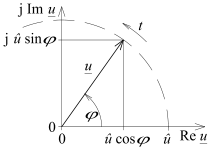
Harmonic oscillations can be represented by the rotation of a pointer whose length corresponds to the amplitude of the oscillation. The instantaneous displacement is the projection of the pointer onto one of the coordinate axes. If the complex number plane is used to represent the pointer, either the real part or the imaginary part corresponds to the instantaneous displacement, depending on the definition.

The angular frequency ω $\omega$ is the rate of change of the phase angle φ $\varphi$ of the rotating pointer (see adjacent figure). In adaptation to the unit of the angular frequency, the angle should be given in radians.

$\omega ={\frac {{\text{d}}\varphi }{{\text{d}}t}}$

The pointer model is applicable to all types of oscillations (mechanical, electrical, etc.) and signals. Since one period of oscillation corresponds to one full revolution of the pointer, and the full angle $2\pi$ is , the angular frequency of a harmonic oscillation is always $2\pi$ times its frequency. Often, the specification of the angular frequency is preferred over the frequency, since many formulas in oscillation theory can be represented more compactly using the angular frequency due to the occurrence of trigonometric functions whose period $2\pi$ is by definition : e.g., in the case of a simple cosine, the period is 2 π {\displaystyle 2\pi }. For example, for a simple cosine oscillation: instead of $y={\hat {y}}\cdot \cos(\omega t)$ $y={\hat {y}}\cdot \cos(2\pi f\,t)$ .

In the case of circular frequencies which are not constant in time, the term instantaneous circular frequency is also used.

Pointer representation of a harmonic oscillation in the complex plane (using the example of an AC voltage ${\underline {u}}$ ) with the time-dependent argument φ $\varphi =\omega t+\varphi _{0}$ .

Use in vibration theory

A harmonic oscillation can be $\omega$ described in general terms as a function of the angular frequency ω

$x(t)=x_{0}\,\sin \left(\omega t+\varphi _{0}\right)$

It can be represented, as is common in electrical engineering, by the real and imaginary parts of a complex pointer ${\underline {x}}$ rotating at constant angular velocity in the Gaussian number plane as a function of angular frequency and time. The time-dependent angle φ $\varphi (t)=\omega t+\varphi _{0}$ of the complex pointer is called the phase angle.

${\underline {x}}(t)=x_{0}\,e^{i(\omega t+\varphi _{0})}=x_{0}\,(\cos(\omega t+\varphi _{0})+i\sin(\omega t+\varphi _{0}))$

The connection with sine and cosine results from Euler's formula.

Characteristic circuit frequency and natural circuit frequency

Oscillating systems are described by the characteristic angular frequency and the natural angular frequency. An undamped freely oscillating system oscillates with its characteristic angular frequency ω $\omega _{0}$ , a damped system with no external excitation oscillates at its natural angular frequency ω $\omega _{d}$ . The natural angular frequency of a damped system is always less than the characteristic angular frequency. In mechanics, the characteristic angular frequency is also referred to as the undamped natural angular frequency.

For the example of an electric resonant circuit, with the resistance the inductance and the capacitance for the characteristic frequency:

$\omega _{0}={\frac {1}{\sqrt {LC}}}$

For a spring pendulum with spring stiffness and mass following applies to the characteristic frequency:

$\omega _{0}={\sqrt {\frac {c}{m}}}$

and with the decay constant δ $\delta =R/{(2L)}$ or δ $\delta =d/{(2m)}$ for the natural angular frequency:

$\omega _{d}={\sqrt {\omega _{0}^{2}-\delta ^{2}}}$ .

For further examples see torsion pendulum, water pendulum, thread pendulum.

Complex angular frequency

From the complex pointer representation of a harmonic oscillation

${\underline {x}}(t)=x_{0}\,e^{\mathrm {i} \omega t}$

results with the usual approach

${\underline {x}}(t)=x_{0}\,e^{st}$

the generalization to the complex angular frequency $s=\sigma +\mathrm {i} \,\omega$ with the real part σ $\sigma$ and the angular frequency ω $\omega$ . By the complex angular frequency not only a constant harmonic oscillation with σ $\sigma =0$ represented, but also a damped oscillation with σ $\sigma <0$ and an excited oscillation with σ $\sigma >0$ . A classical application of the complex angular frequency is the extended symbolic method of AC.

A damped oscillation can be represented as a complex pointer with the constant complex angular frequency s as follows:

${\underline {x}}(t)=x_{0}\,e^{st}=x_{0}\,e^{(\sigma +\mathrm {i} \omega _{d})t}=x_{0}\,e^{\sigma t}e^{\mathrm {i} \omega _{d}t}=x_{0}\,e^{\sigma t}(\cos(\omega _{d}t)+\mathrm {i} \sin(\omega _{d}t))$

Here ω $\omega _{d}$ is the natural angular frequency of the oscillatory system and σ $\sigma$ is equal to the negative value of the decay constant: σ $\sigma =-\delta$ (see the previous section for details).

In the Laplace transform, the complex angular frequency $s=\sigma +\mathrm {i} \omega$ has a more general meaning as a variable in the image domain of the transform F(s) for representing arbitrary time functions and transfer functions in the complex frequency plane ("s-plane").