Group (mathematics)

In mathematics, a group is a set of elements together with a conjunction that assigns a third element of the same set to every two elements of the set, satisfying three conditions, the group axioms: the associative law, the existence of a neutral element, and the existence of inverse elements.

One of the best known groups is the set of integers with addition as the link. The mathematical branch devoted to the study of group structure is called group theory. It is a subfield of algebra. The applications of groups, even outside mathematics, make them a central concept in contemporary mathematics.

Groups share a fundamental kinship with the idea of symmetry. For example, the symmetry group of a geometric object embodies its symmetric properties. It consists of the set of those mappings (e.g. rotations) which leave the object unchanged, and the succession of such mappings as a linkage. Lie groups are the symmetry groups of the Standard Model of particle physics, point groups are used to understand symmetry at the molecular level in chemistry, and Poincaré groups can express the symmetries underlying special relativity.

The concept of group arose from Évariste Galois' investigations of polynomial equations in the 1830s. Following contributions from other mathematical fields such as number theory and geometry, the notion of group was generalized. By 1870 it was firmly established and is now treated in the distinct field of group theory. To study groups, mathematicians have developed special notions to break groups down into smaller, more easily understood components, such as subgroups, factor groups, and simple groups. In addition to their abstract properties, group theorists also study ways in which groups can be expressed concretely (representation theory), both for theoretical investigations and for concrete calculations. A particularly rich theory has been developed for finite groups, culminating in the classification of finite simple groups in 1983. These play a comparable role for groups as prime numbers do for natural numbers.

The turns of a Rubik's Cube form a group.

Introductory example

One of the best known groups is formed by the set of integers , $\{\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\}$ commonly denoted by , $\mathbb {Z}$ together with addition.

The set of integers together with addition satisfies some basic properties:

For two integers and the sum is again an integer. On the other hand, if you were to divide two integers together, the result would mostly be a rational number and no longer an integer. Since this cannot happen with addition, the integers are said to be completed under addition.
For all integers , and the associative law applies

(a + b) + c = a + (b + c) .

In words, this means that it doesn't matter whether you first add and or and , the result is the same. This property is called associativity.

For any integer following applies

0 + a = a + 0 = a .

Therefore, the addition with zero does not change the initial number. Therefore, zero is called the neutral element of addition.

For every integer there exists an integer such that . That is, for every integer there exists an integer such that their sum is zero. In this case, the number is called the inverse element of and is notated as

These four properties of the set of integers together with their addition are generalized to other sets with a suitable operation in the definition of the group.

Examples

In the following some examples of groups are given. Thus groups of numbers, a group with exactly one element and examples of cyclic groups are given. Further examples of groups can be found in the list of small (finite) groups.

sets of numbers

The set of integers together with addition forms an (abelian) group. Together with multiplication, however, the set of integers is not a group (the inverse element of 2 would be 1/2).
The set of rational numbers $\mathbb {Q}$ respectively the set of real numbers $\mathbb {R}$ with addition is a group. Together with multiplication, the sets $\mathbb{Q} \setminus \{0\}$ and $\R \setminus \{0\}$ also groups.

The trivial group

→ Main article: Trivial group

The set which has only one element $\{e\}$ can be considered as a group. Since every group has one neutral element, this one element must then be taken to be the neutral element. So then e * e = e . By means of this equality, the remaining group axioms can also be proved. The group with exactly one element is called the trivial group.

Cyclic groups

→ Main article: Cyclic group

A cyclic group is a group whose elements can be represented as powers of one of its elements. Using multiplicative notation, the elements of a cyclic group are

$\ldots , a^{-3}, a^{-2}, a^{-1}, e = a^{0}, a, a^2, a^3, \ldots$ ,

where $a^{-2} = a^{-1} \cdot a^{-1}$ and denotes the neutral element of the group. The element is called the producer or primitive root of the group. In additive notation, an element is a primitive root if the elements of the group are represented by

$\ldots, -a -a, -a, 0, a, a+a, \ldots$

can be displayed.

For example, the additive group of integers considered in the first section is a cyclic group with primitive root . This group has infinitely many elements. In contrast, the multiplicative group of nth complex unit roots has finitely many elements. This group consists of all complex numbers that satisfy the equation

$z^{n}=1$

satisfy. The group elements can be visualized as vertices of a regularn-corner. For n = 6 this is done in the graph on the right. The group operation is the multiplication of the complex numbers. So in the right-hand picture, multiplying by corresponds to rotating the polygon counterclockwise by $60^{\circ }$ .

Cyclic groups have the property of being uniquely determined by the number of their elements. That is, two cyclic groups each with elements are isomorphic, so a group isomorphism can be found between these two groups. So, in particular, all cyclic groups with infinitely many elements are equivalent to the cyclic group $(\Z,+)$ of integers.

Symmetrical groups

→ Main article: Symmetric group

The symmetric group $S_{n}$ consists of all permutations (permutations) of an -elementary set. The group operation is the composition $\circ$ (successive execution) of the permutations, the neutral element is the identical mapping. The symmetric group $S_{n}$ is finite and has order $n!$ . It is not abelian for . $n\geq 3$

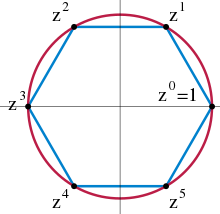
The 6th complex unit roots can be taken as a cyclic group.