Great circle
A great circle is the largest possible circle on the surface of a sphere. Its center always coincides with the center of the sphere, and a cut on the great circle divides the sphere into two ("equal-sized") halves in every case. Since there are an infinite number of ways to cut a sphere so that the plane of the cut meets the center of the sphere, there are also an infinite number of great circles.
Great circles play an important role, for example, in geography as well as in shipping and aviation. They are also used to determine time zones. Spherical geometry contains great circles as an elementary component. The understanding of orthodromes as the shortest connection between two points on a spherical surface is essential for the understanding of "rectilinear", unaccelerated (departure from the concept of gravitation) motion in curved space (general relativity, space curvature).
In the geographic coordinate system of the earth there are special cases of great circles. They are specially positioned great circles. These special cases are the equator (here solid blue line) and the meridians (here yellow line). The equator is the great circle that separates the globe in the middle between the south and north poles. The meridians go through the south and the north pole. On them lie the meridians, each extending from the north to the south pole, such as the prime meridian (0°) and the 180° meridian. The meridians are also called longitudes. On the other hand, the circles of latitude (dotted lines here), with the exception of the equator, are not great circles, but smaller than the maximum circumference of the sphere. Therefore they are called minor circles.
On the great circles of the earth one minute of arc corresponds to one nautical mile, abbreviated sm (nm or NM). It can be calculated (i.e. as a "minute of longitude" or as a "minute of latitude at the equator") with 1852 metres at an assumed circumference of the earth of 40,000 km. The mean radius of the earth is 6371 km.
The shortest connection between two points on a spherical surface - the so-called orthodrome - is always part of a great circle (the so-called main arc). This is why shipping routes and especially air routes usually run along great circles. Traversing the globe on orthodromes is called great circle sailing; with starting and destination points at similar latitudes, the "great circle courses" run over somewhat larger latitudes (e.g. Munich-Peking over Siberia).
On the Earth's ellipsoid and other surfaces, the orthodromic is called a geodesic line. It is a curve of higher order (deviation from the great circle of a sphere some per mille) and corresponds to the course of a tautly stretched, frictionless thread. On the earth ellipsoid, e.g. according to WGS84, the initial course and distance are calculated according to the formula of Thaddeus Vincenty.
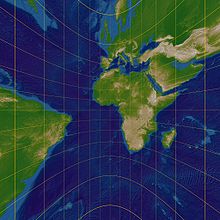
Map in gnomonic projection: great circles appear straight as far as shown.
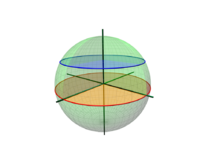
Large circle (red) and small circle (blue)
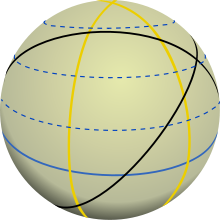
Various large circles (solid lines). The yellow great circles here are longitude circles. Inclination of the 2 black great circles against the equator (blue) approx. 55° and 60°.
Display on maps
Since many maps (e.g. the Mercator map) are drawn in such a way that the latitudes appear as straight, horizontal lines, the flight paths appear curved despite their shortness and run further polewards (see also rhumb lines). To simplify drawing, there are special great circle maps (see gnomonic projection) on which all great circles appear as straight lines, but the surrounding area is somewhat distorted. Shortest air routes and long shortest ship routes (e.g. when crossing the Atlantic) can be shown as straight lines on a gnomonic map. The compass course to be followed changes continuously and can be read on the map as the angle between the meridian and the course line.
On nautical charts, the latitude is plotted on the right and left edges, i.e. the respective section of the relevant longitude great circle. Here the navigator can take a distance with the compass (1 minute of arc = 1 nautical mile = 1.852 km) and transfer it to the chart to plot positions and courses.
Calculation
The angle between points A and B with latitude coordinates φ 
and longitude coordinates λ 
on the great circle is calculated as follows:
If 
is given in radians, the great circle distance d between the two points can be calculated from the earth radius rE:
The great circle distance is at most half the circumference of the earth.
The angle of intersection of the great circle of A and B with the meridian at point A is called the heading angle ω 
. It is calculated by:
For easterly courses (λB > λA) the course angle is between 0° and 180°, for westerly courses (λB < λA) the course angle is between 180° and 360°. In contrast to plane geometry, the course angles from A to B and from B to A do not differ by 180°. In the extreme case, when the great circle passes over the poles, the two course angles can even be equal.
