Gravitational constant

The gravitational constant (formula symbol or γ $\gamma$ ) is the fundamental natural constant that determines the strength of gravity. In Isaac Newton's law of gravitation, it directly gives the strength of the gravitational force between two bodies as a function of their distance and masses; in Albert Einstein's general theory of relativity, it determines the curvature of four-dimensional spacetime and thus the course of all gravitationally related phenomena. It is of fundamental importance for the description of astronomical quantities and processes. The value of the gravitational constant is

$G=(6{,}674\,30\pm 0{,}000\,15)\cdot 10^{-11}\,\mathrm {\frac {m^{3}}{kg\cdot s^{2}}} ,$

whereby already the fourth decimal place is uncertain.

Value and units

In the International System of Units (SI), the value according to the current CODATA 2018 recommendation is:

$G=6{,}674\,30(15)\cdot 10^{-11}\,\mathrm {\frac {m^{3}}{kg\cdot s^{2}}}$

(i.e., with an estimated standard uncertainty of $0{,}000\,15\cdot 10^{-11}\,\mathrm {m} ^{3}/(\mathrm {kg} \cdot \mathrm {s} ^{2})$ ).

In the CGS system of units has the value

$G=6{,}674\,30(15)\cdot 10^{-8}\,\mathrm {\frac {cm^{3}}{g\cdot s^{2}}} .$

The gravitational constant can also be expressed using other natural constants, for example Planck's reduced quantum of action $\hbar$ and the speed of light {"natural units"). According to CODATA 2018, the value is:

$G=6{,}708\,83(15)\cdot 10^{-39}\,{\frac {\hbar c}{(\mathrm {GeV} /c^{2})^{2}}}$

Compared to other fundamental forces of physics, gravity is a very weak interaction, which is expressed in the small value of the gravitational constant. For example, calculating the amount of the ratio between the gravitational force and the electrostatic force between two protons, we get regardless of the distance:

$\left|{\frac {F_{\text{Gravitation}}}{F_{\text{elektrisch}}}}\right|={\frac {Gm_{\text{Proton}}^{2}}{e^{2}/(4\pi \varepsilon _{0})}}\approx 10^{-36}$

Measurements

The gravitational force between the earth and another object, i.e. its weight, can be measured very accurately, but in order to determine the gravitational constant with the same accuracy, one would have to know the mass of the earth or better the whole mass distribution in the earth reliably. But this is not given, so that in order to measure , the extremely small gravitational attraction between bodies of known mass must be determined in the laboratory. For example, the gravitational attraction between two bodies of mass 100 kg each at a distance of 1 m is less than 10-9 (one billionth) of their weight, and all other matter in the laboratory or outside it also exerts gravitation on the test bodies. These measurements are therefore difficult. Even the smallest differences in temperature, air currents, irregularities in the material or creep of the material, even the number of vehicles in the parking lot in front of the institute building, falsify the results.

Current status

A value for with eight-digit accuracy, as achieved for other natural constants long ago, would thus require here a reduction of such possible perturbations to 10-17 (one hundred billionth) of the weight force of the bodies involved. This has not yet been achieved. Five-digit accuracy is thus the highest, it was given for a measurement of from the year 2000. However, from the last three decades alone, there are a total of 13 other measurement results from laboratories around the world with various apparatuses, some of which state similarly high accuracy, but which nevertheless differ by up to almost ten times the uncertainty ranges stated in each case. It is assumed that the individual apparatuses still have undetected weak points.

As a result, the relative uncertainty in the value of cannot be pushed below 2.2 - 10-5 at present. Thus, is currently the one with the lowest measurement accuracy among the fundamental constants of nature. For comparison, the Rydberg constant is known in SI units with a relative uncertainty of 1.9 - 10-12, which is more than a million times more accurate.

The - in comparison - low accuracy of and the too large scattering range of the single results are regarded as deficiencies. Apart from unrecognized weaknesses of the measuring apparatuses, the scattering width could also point to an aspect of gravitation which is not yet understood. The inaccuracy limits the possibility of determining the mass of a celestial body from its gravity. To do this, the celestial body must be orbited by a companion whose orbital radius and orbital angular frequency ω {\displaystyle $\omega$ are known, so that the gravitational parameter μ $\mu = r^3 \omega^2$ determined. This is often possible with high accuracy, for the Earth, for example, with up to 10-digit accuracy (see WGS 84). Then the mass of the celestial body is given by $M=\mu /G$ (see Kepler's laws). Despite the uncertainty in much more accurate than estimating the mass from the diameter and the density profile inside the celestial body.

In recent experiments, the gravitational constant is measured using two different methods by varying the experimental setup of the pendulum balance:

Vibration time method: a gold-plated quartz block on a fiberglass and two steel balls, each weighing 778 grams, change torsional vibrations, resulting in gravitational constants of $6{,}674\,184\cdot 10^{-11}\,\mathrm {{m^{3}}\,{kg^{-1}\,s^{-2}}}$ ±11.64 ppm.
Method for measuring angular acceleration: In the second experimental setup, both masses (quartz block and steel balls) are allowed to rotate independently and the turntable is tracked to compensate for torsion, resulting in no rotation angle, but angular acceleration ("angular-acceleration-feedback method") is measured to compensate for the angle of rotation, from which a value of $6{,}674\,484\cdot 10^{-11}\,\mathrm {{m^{3}}\,{kg^{-1}\,s^{-2}}}$ ±11.61 ppm was derived.

In previous experiments, the standard deviation was ±47 ppm, so it was improved by ±36 ppm.

The Cavendish Experiment

The first measurement of the gravitational force between two masses of known size was made by Henry Cavendish in 1798 with the help of a specially invented gravitational balance. The balance consisted of two spherical test masses with a combined mass (in today's units) of = 1.46 kg, which were connected to form a dumbbell and suspended from a torsion wire so that they could perform free horizontal torsional oscillations. Two large spheres of total mass $M_{c}=316\,\mathrm {kg}$ , equally spaced r_m close to each of the test masses, produced the attractive force that deflected the test masses about 1° from rest. From the angle of deflection, the torsional force F_c determined, which balanced the attractive force of the large and small balls at this distance. The necessary knowledge of the torsional stiffness of the wire was obtained from the period of the torsional vibration.

From Cavendish's measured values, the following formula is obtained

${\frac {F_{c}\,r_{m}^{2}}{m\,M_{c}}}=G$

a value for the constant

$G_{\mathrm {Cavendish} }=6{,}754\cdot 10^{-11}\,\mathrm {{m^{3}}\,{kg^{-1}\,s^{-2}}} .$

This falls short of today's figure by only 1.2 percent.

However, the concept of a gravitational constant was not yet common in Cavendish's time, rather Newton's law of gravitation was used exclusively in the form of proportionalities. Accordingly, he considered the ratio of the two forces $F_{c}$ and F_E , by which the small spheres are attracted to the large ones and to the earth, respectively. According to Newton:

$\frac {F_c} {F_E} = \frac { M_c} {M_E}\ \frac {r_E^2} {r_m^2}$

F_E is nothing else than the (total) weight of the small spheres, so that the earth mass $M_{E}$ the only unknown in this. Cavendish was able to determine the mass of the Earth from his measurement data. The physically incorrect and, strictly speaking, meaningless formulation that Cavendish "weighed the earth" became popular.

After the mass of the earth, implicitly the value of the gravitational constant, was known, the masses of other celestial bodies of the solar system could be determined.

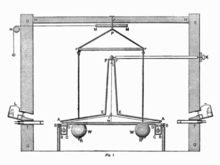
Cavendish Experiment (1798)