Graphene
![]()
This article is about the material graphene. Graphene is also the plural of graph.
Graphene [gʁa'feːn] (emphasis on the second syllable: graphene) is the name for a modification of carbon with a two-dimensional structure in which each carbon atom is surrounded by three others at an angle of 120°, forming a honeycomb pattern. Since carbon is tetravalent, there must be two double bonds per "honeycomb", but these are not localized. This is a concatenation of benzene rings, as often occurs in aromatic compounds. Although a single benzene ring has three double bonds in the representation of the valence bar formulae, connected benzene rings in this representation formally have only two double bonds per ring. Therefore, the structure can be better described by representing the delocalized bonds as a large circle in the benzene ring. The bonding ratios in graphene are described in the graphene structure. Graphene can be described as a polycyclic aromatic hydrocarbon. At the "edge" of the honeycomb lattice, other atomic groups must be docked, but - depending on its size - they hardly change the properties of graphene.
In theory, single-layer carbon films, graphenes, were used for the first time to describe the structure and electronic properties of complex materials made of carbon.
However, infinitely extended and everywhere flat strictly two-dimensional structures are not possible due to a rigorous mathematical theorem, the Mermin-Wagner theorem and its variants, which has been shown to be thermodynamically unstable.
This is why chemists and physicists were astonished when Konstantin Novoselov, Andre Geim and their co-workers announced the creation of free, single-layer graphene crystals in 2004. Their unexpected stability could be explained by the existence of metastable states or by the formation of an irregular crumpling of the graphene layer.
In 2010, Geim and Novoselov were awarded the Nobel Prize in Physics for their research, having not only made crucial contributions to the representation of these systems, but also discovered many of their unusual properties.
Mentally, by stacking such single-layered layers, the three-dimensional structure of graphite can be generated, to which graphene is closely related structurally. If, on the other hand, one imagines the single-layered layers rolled up, one obtains stretched carbon nanotubes. Also mentally, one can replace some of the six-membered rings with five-membered rings, causing the flat surface to curve into a spherical surface and yielding fullerenes at certain number ratios: For example, if one replaces 12 of 32 rings, the smallest fullerene (C60) is formed. Theoretically, single-layer films of other tetravalent elements such as silicon and germanium are also possible. In 2012, silicene layers were indeed experimentally detected in the form of a slightly corrugated single-layer of silicon.

Graph model
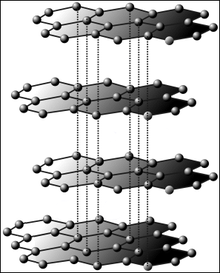
Relationship between graphene and graphite

Play media file Introductory (and at the same time summarizing) animated film (text in English): Electronic band structure and Dirac cone; lattice effects
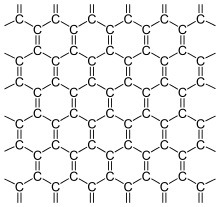
Valence stroke formula
Structure
All carbon atoms of graphene are sp2-hybridized, which means that each carbon atom can form three equivalent σ-bonds to other C atoms. This results in a honeycomb structure also known from the layers of graphite. The carbon-carbon bond lengths are all equal and are 142 pm. The third, non-hybridized 2p orbitals are perpendicular to the graphene plane, as in graphite, and form a delocalized π-bond system.
Consequently, graphene consists of two equivalent sublattices A and B, to which the carbon atoms are assigned. The sublattices are shifted with respect to each other by the bond length 




Graphene can be understood as a single crystal on the one hand, and as a giant molecule on the other. Similarly, smaller molecules such as benzene, hexabenzocoronene or naphthalene can be seen as hydrogen-substituted graphene fragments.
Properties
| Properties of graphene | |
| Property | Value |
| Mass per unit area | 7,57 × 10-7 kg-m-2 |
| E-modulus | approx. 1020 GPa |
| Tensile strength | 125 GPa |
| attenuation of visible light | 2,3 % |
| Layer thickness | 3,35 × 10−10 m |
| Thermal conductivity | approx. 5000 W/(m-K) |
| Electrical resistivity | 31 Ω |
Graphene has unusual properties that make it interesting for both basic research and applications, especially in physics.
For example, graphene face single crystals are exceptionally stiff and strong within the faces. Its modulus of elasticity of about 1020 GPa is equal to that of normal graphite along the basal planes and almost as large as that of diamond. Its tensile strength of 1.25×1011 Pa is the highest ever determined and about 125 times that of steel. A ribbon of graphene 1 m wide and 3.35 × 10-10 m thick, that is, of one atomic layer, has therefore a tensile strength of 42 N. A ribbon for a space elevator made of graphene with a constant cross-sectional area would only be loaded to 87.3% of its tensile strength at the geostationary orbit altitude of 35,786 km.
Assuming monocrystalline graphite with a density of 2260 kg-m-3 and a layer spacing of 3.35 × 10-10 m, multiplication calculates a mass per unit area for graphene of 7.57 × 10-7 kg-m-2. One square kilometer thus weighs 757 g. "A graphene hammock one square meter in size could support a four-kilogram cat - and itself weigh only as much as a single cat whisker."
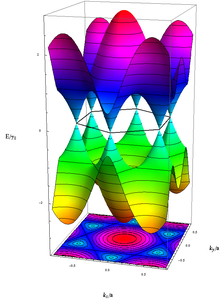
Graphene behaves as an electrical conductor due to the lack of a band gap, see the figure below for the energy of electrons in graphene. However, an artificial band gap in graphene can be created by "cutting" a so-called gate into the layer with a maximum width of 10 nm.
Measurements have shown that a single graphene layer attenuates light by about πα ≈ 2.3% (with fine structure constant α), over the entire visible spectrum.
Pseudo-relativistic behaviour
The electrical properties of graphene can be well described by a tight-binding model. Within the framework of this model, the energy of electrons with wavenumber 

With the nearest-neighbor hopping energy γ 




Here denotes 



Unusual quantum Hall effect
Because of the peculiarities in dispersion, in this material the staircase structure of the integer quantum Hall plateaus, σ 

Stiffness and temperature dependence
Graphene is extremely stiff in the layer direction because the sp2 bond between neighbouring atoms is comparable in strength to the sp3 bond of diamond. Accordingly, it is generally expected - and this corresponds to the experiment - that the properties of graphene which are of interest for applications are not only valid at absolute temperature zero, i.e. at -273.15 °C, but remain valid at room temperature.
One such property is thermoelectricity: a temperature gradient in graphene planes causes an electric field strength due to a decoupling of the temperature of the electrons from that of the lattice. Electric voltage when graphene is illuminated had been observed before, but the cause was thought to be photovoltaics. The fact that the decoupling can still be observed at room temperature is due to the rigidity of the lattice: the elementary vibrational excitations of the lattice (phonons) are so high-energy that the electrons rarely produce such a phonon.
Elastic behaviour and pseudo magnetic field
In July 2010, a publication in the American scientific journal Science reported extremely strong pseudo-magnetic fields. By elastic deformation, tiny triangular bubbles of 4 nanometers to 10 nanometers in size were created in graphene, in which the electrons moved as if a magnetic field of about 300 teslas was acting on them. It turned out that, unlike the effect of a real magnetic field, the observed effect does not affect the actual spin of the electron, but instead affects the pseudo-spin just mentioned, which is related to the existence of two different equivalent base atoms in the honeycomb structure. This pseudospin has a similar interaction with the pseudomagnetic field as real spins have with real magnetic fields, because these also generate "two-level systems". The experiments around the "pseudo-quantum Hall effect" generated in this way were based on theoretical predictions, which were thus confirmed.
Spin streams
In April 2011, A. Geim and coworkers published an article describing strong spin currents and current-induced magnetism near the Dirac point, i.e., near the meeting point of the conduction band and the valence band. This opens up the prospect of applications in spintronics.
Chemical functionalization and large-scale EU project
In 2013, the EU announced a major new project ("flagship project") on graphene, on which researchers in many Member States will collaborate, especially physicists and chemists. It is possible, for example, to "break" double bonds in graphene - every second bond is such a bond - and replace them with two single bonds, to which various organic molecules can then be attached: this allows the properties of the system to be specifically influenced.
Hydrodynamic behaviour with unusual properties
In 2016, a so-called hydrodynamic ("liquid-like") behaviour of the electrons in graphene was found, but with extraordinary properties: For example. the Wiedemann-Franz law, otherwise valid for metallic systems, that the ratio of thermal and electrical conductivity divided by the Kelvin temperature T is equal to a universal constant in metallic systems, is violated in graphene, in that when the Fermi energy approaches the overlap point, the thermal conductivity becomes much too large (i.e. the specific thermal resistance becomes much too small). Moreover, in this electron fluid (technical term: Dirac fluid) one observes an unusual tendency to form vortex structures.
Questions and Answers
Q: What is graphene?
A: Graphene is one of the forms of carbon, with a two-dimensional honeycomb or 'chicken wire' structure made up of carbon atoms and their bonds.
Q: How is graphene related to graphite?
A: Graphite is many graphene sheets stacked together - three million graphene sheets stacked to form graphite would be only one millimetre thick.
Q: Who coined the term 'graphene'?
A: The term 'graphene' was coined as a combination of graphite and the suffix '-ene' by Hanns-Peter Boehm in 1962.
Q: What did Sir Andre Geim and Sir Konstantin Novoselov win the Nobel Prize in Physics for 2010 for?
A: Sir Andre Geim and Sir Konstantin Novoselov won the Nobel Prize in Physics for 2010 "for groundbreaking experiments regarding the two-dimensional material graphene".
Q: What are some possible applications of graphene?
A: Possible applications of graphene include supercapacitors.
Q: What other forms or allotropes does carbon have besides graphene?
A: Other forms or allotropes that carbon has besides graphene include diamonds, graphite, charcoal, fullerene and carbon nanotubes.
Search within the encyclopedia