Graph of a function

In mathematics, the graph of a function is the set of all ordered pairs (x,f(x)) of the elements the definition set and the corresponding function values f(x) .

Sometimes these pairs can be interpreted as points in the drawing plane or in the visual space, they are also called curve, curve progression or also function graph.

Graph of the function $f(x)=x^{3}-9x$

Graph of function $f(x,y)=\sin \left(x^{2}\right)\cos \left(y^{2}\right)$

Definition

The graph of a function $f\colon D\to Z$ with definition set and target set is the set

$G_{f}=\{(x,f(x))\in D\times Z\mid x\in D\}$ .

The graph is thus a special subset of the Cartesian product of the definition set and the target set. It consists of all pairs where the first component is an element of the definition set and the second component is the element of the target set assigned to this element by the function.

Special cases and examples

The graph of a function $f\colon D\to \mathbb {R}$ with $D\subseteq \mathbb {R}$ is a subset of $\mathbb {R} \times \mathbb {R} =\mathbb {R} ^{2}$ and thus can be taken to be a set of points or a geometric figure in the plane. Examples are:

The graph of a linear function $f\colon \mathbb {R} \to \mathbb {R} ,x\mapsto ax+b$ is a straight line.
The graph of a quadratic function $f\colon \mathbb {R} \to \mathbb {R} ,x\mapsto ax^{2}+bx+c$ with $a\neq 0$ is a parabola.
The graph of the reciprocal function $f\colon \mathbb {R} \setminus \{0\}\to \mathbb {R} ,x\mapsto {\tfrac {1}{x}}$ is a hyperbola.

The graphs of functions $f\colon \mathbb {R} ^{2}\to \mathbb {R}$ or $f\colon \mathbb {R} \to \mathbb {R} ^{2}$ are subsets of $\mathbb {R} ^{3}$ and can still be represented pictorially as spatial figures as well. Examples are:

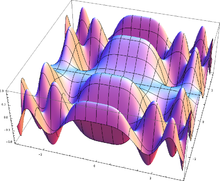
The graph of a continuous function $f\colon \mathbb {R} ^{2}\to \mathbb {R}$ is a surface in three-dimensional space. For example, the graph of the function is $f(x,y)=x^{2}+y^{2}$ an elliptic paraboloid.
The graph of a continuous function $f\colon \mathbb {R} \to \mathbb {R} ^{2}$ is a graph in three-dimensional space. For example, the graph of the function is $f(t)=(\sin t,\cos t)$ a helical line.

Questions and Answers

Q: What is a graph?

A: A graph is a picture designed to express words, particularly the connection between two or more quantities.

Q: How is the relationship between two numbers or measurements shown on a simple graph?

A: The relationship between two numbers or measurements is shown in the form of a grid.

Q: What is a Cartesian coordinate system?

A: A Cartesian coordinate system is a rectangular graph where the two measurements are arranged into two different lines at right angles to one another.

Q: How are the vertical and horizontal axes arranged in a rectangular graph?

A: The vertical axis goes up, while the horizontal axis goes right.

Q: Where do the lines or axes meet in a rectangular graph?

A: The lines or axes meet at their ends in the lower left corner of the graph.

Q: What are tick marks in a graph?

A: Tick marks are markings along each axis that act like a ruler drawn on paper to indicate each measurement.

Q: What is the difference between a graph and a chart or diagram?

A: A graph relates one quantity to other quantities while a chart or a diagram may not. Flowcharts and tree diagrams are examples of charts or diagrams that are not graphs.