Gradient

The gradient as an operator of mathematics generalizes the known gradients, which describe the course of physical quantities. As a differential operator, it can be applied to a scalar field, for example, and in this case will yield a vector field called a gradient field. The gradient is a generalization of the derivative in multidimensional analysis. To better distinguish between the operator and the result of its application, such gradients of scalar field quantities are also called gradient vectors in some sources.

In Cartesian coordinates, the components of the gradient vector are the partial derivatives at the point , the gradient therefore points in the direction of greatest change. The magnitude of the gradient indicates the value of the largest rate of change at that point.

For example, if one interprets the relief map of a landscape as a function h(x,y), which assigns to each location the elevation at that location, then the gradient of at the location (x,y) is a vector pointing in the direction of the greatest elevation increase of The magnitude of this vector indicates the largest slope at this point.

The gradient is studied together with other differential operators such as divergence and rotation in vector and tensor analysis, subfields of multidimensional analysis. They are formed with the same vector operator, namely the Nabla operator $\nabla$ (sometimes also ${\vec {\nabla }}$ or ${\underline {\nabla }}$ to indicate that the Nabla operator can be understood alternatively as a vector).

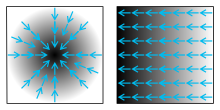
Two scalar fields, displayed as gray shading (darker color corresponds to larger function value). The blue arrows on them symbolize the corresponding gradient.

Definition

On $\mathbb {R} ^{n}$ let be $\langle {\cdot },{\cdot }\rangle$ given the scalar product ⟨ The gradient $\operatorname {grad}$ of the totally differentiable function $f\colon \mathbb {R} ^{n}\to \mathbb {R}$ at the point ${\vec {a}}\in \mathbb {R} ^{n}$ is the point given by the requirement

$\mathrm {d} f({\vec {a}}){\vec {h}}=\langle \operatorname {grad} f({\vec {a}}),{\vec {h}}\rangle \quad ({\vec {h}}\in \mathbb {R} ^{n})$

uniquely determined vector $\operatorname {grad} f({\vec {a}}).$ The operator $\mathrm {d}$ is the total differential or Cartan derivative.

For differentiable functions gradient has the defining property

$f({\vec {y}})-f({\vec {a}})=\mathrm {grad} f({\vec {a}})[{\vec {y}}-{\vec {a}}]+{\mathcal {O}}(|{\vec {y}}-{\vec {a}}|)$ for ${\vec {y}}\to {\vec {a}}$

The Landau symbol $\mathcal{O}(x)$ represents terms that grow slower than , and $\ldots [{\vec {h}}]$ represents a linear function of ${\vec h}$ If the gradient exists, it is unique and can be derived from

$\mathrm {grad} f({\vec {a}})[{\vec {h}}]=\left.{\frac {\mathrm {d} }{\mathrm {d} s}}f({\vec {a}}+s{\vec {h}})\right|_{s=0}=\lim _{s\to 0}{\frac {f({\vec {a}}+s{\vec {h}})-f({\vec {a}})}{s}}=({\vec {h}}\cdot \nabla )f$

where $\nabla$ is the nabla operator. This is also how gradients are defined for scalar, vector, and second level tensor fields, or nth level tensor fields in general.

For a scalar field, it follows that $\mathrm {grad} f=\nabla f$ ; therefore, one often writes $\nabla f$ (pronounced "Nabla ") instead of $\operatorname {grad} {f}$ .

Coordinate representation

The gradient also has different representations in different coordinate systems.

Cartesian coordinates

In $\mathbb {R} ^{n}$ with the standard Euclidean scalar product, is $\operatorname {grad} f(a)$ the column vector

$\operatorname {grad} (f)={\frac {\partial f}{\partial x_{1}}}{\hat {e}}_{1}+\cdots +{\frac {\partial f}{\partial x_{n}}}{\hat {e}}_{n}={\begin{pmatrix}{\frac {\partial f}{\partial x_{1}}}\\\vdots \\{\frac {\partial f}{\partial x_{n}}}\end{pmatrix}}.$

The entries ∂ ${\tfrac {\partial f}{\partial x_{i}}}$ are the partial derivatives of in $x_{i}$ direction.

Calculation example

Given a scalar field by $f(x,y)=2x^{2}-y^{2}$ in the xy plane. It has partial derivatives ∂ ${\tfrac {\partial f}{\partial x}}=4x$ and ∂ ${\tfrac {\partial f}{\partial y}}=-2y$ and it follows $\operatorname {grad} (f)=\nabla f={\tfrac {\partial f}{\partial x}}{\hat {e}}_{x}+{\tfrac {\partial f}{\partial y}}{\hat {e}}_{y}=4x{\hat {e}}_{x}-2y{\hat {e}}_{y}$ or in vector representation $\textstyle \operatorname {grad} (f)=\nabla f={\begin{pmatrix}4x\\-2y\end{pmatrix}}.$

For example, for the point P(2|1) the gradient vector is ${\begin{pmatrix}8\\-2\end{pmatrix}}$ . The magnitude is $\left|{\begin{pmatrix}8\\-2\\\end{pmatrix}}\right|={\sqrt {8^{2}+(-2)^{2}}}\approx 8{,}25$ .

Cylinder and sphere coordinates

Display in three-dimensional cylindrical coordinates: $V=V\left(\rho ;\varphi ;z\right)$

$\operatorname {grad} V={\frac {\partial V}{\partial \rho }}{\hat {e}}_{\rho }+{\frac {1}{\rho }}{\frac {\partial V}{\partial \varphi }}{\hat {e}}_{\varphi }+{\frac {\partial V}{\partial z}}{\hat {e}}_{z}$

Display in three-dimensional spherical coordinates: $V=V\left(r;\vartheta ;\varphi \right)$

$\operatorname {grad} V={\frac {\partial V}{\partial r}}{\hat {e}}_{r}+{\frac {1}{r}}{\frac {\partial V}{\partial \vartheta }}{\hat {e}}_{\vartheta }+{\frac {1}{r\sin \vartheta }}{\frac {\partial V}{\partial \varphi }}{\hat {e}}_{\varphi }$

These are special cases of the gradient on Riemannian manifolds. For this generalization see: Outer derivative.

Orthogonal coordinates

In general orthogonal coordinates the gradient has the representation

$\operatorname {grad} f=\sum _{a}{{\frac {1}{h_{a}}}{\frac {\partial f}{\partial {q_{a}}}}\,{\hat {e}}_{q_{a}}}\,,$

where the $h_{a}$ ${\tfrac {\partial {\vec {r}}}{\partial {q_{a}}}}$ denote the magnitude and ${\hat {e}}_{q_{a}}$ denote the direction of the vector ∂

General curvilinear coordinates

In general curvilinear coordinates the gradient has the representation

$\operatorname {grad} f=\sum _{a}{\frac {\partial f}{\partial q_{a}}}\,{\vec {G}}^{a}\,,$

where ${\vec {G}}^{a}$ is the gradient of the coordinate $q_{a}$

Geometric interpretation

The gradient has a descriptive meaning in the already mentioned case of (two-dimensional) maps, in which height data are registered. The height function is then a scalar field, which assigns a height to each point on the map (characterized by an x- and a y-coordinate). The gradient of this scalar field at a point is a vector pointing in the direction of the steepest slope of the height function, and the magnitude of the gradient corresponds to the magnitude of this slope. The gradient at any point is perpendicular to the contour line (level line) of the height function through that point. In a local minimum or maximum (extremum) or at a saddle point, the gradient is just the zero vector, provided that this extreme point lies in the interior of the considered area.

With the help of the gradient, the increase in any direction can also be determined. This so-called directional derivative is - in contrast to the gradient - a scalar. If one runs in the area in (infinitesimally) small triple steps from a point a to the point b and sums up the product of step length and direction derivative in direction of the step, one receives as result the height difference to the starting point a at the destination point b. This height difference is obviously path independent. This height difference is obviously path-independent. In particular, if the start and end points coincide, one has not changed one's altitude at the end, no matter which path one has taken through the area.

Applications

Conservative forces

→ Main article: Conservative force

In physics, many force fields can be represented as the gradient of a potential. Examples are:

the gravitational force

${\vec {F}}_{\mathrm {Gravitation} }(x,y,z)=-m\operatorname {grad} \Phi (x,y,z)\ ,$

which is the same as for a central mass M

${\vec {F}}_{\mathrm {Gravitation} }(r)=-m\operatorname {grad} \Phi (r)=\operatorname {grad} {\frac {GMm}{r}}=-{\frac {GMm}{r^{3}}}\,{\vec {r}}$

is, or

static electric fields ${\vec {E}}$ in electrodynamics

${\vec {E}}(x,y,z)=-\operatorname {grad} \phi (x,y,z)\ .$

In conservative force fields, one of the factors exploited is that, for sample masses or sample sample loads the path integrals the work ${\textstyle W=\int _{S}{\vec {F}}({\vec {r}})\cdot \mathrm {d} {\vec {r}}}$ along any path through the force field depends only on the starting and ending points of the path, but not on its course, see #integral theorems.

Transport phenomena

Numerous transport phenomena can be traced back to the fact that the associated currents can be expressed as a gradient of a scalar field, with the proportionality factor that occurs being referred to as the transport coefficient or conductivity.

An example is the heat flow ${\vec {j}}_{w}$ in thermodynamics, for which

${\vec {j}}_{w}=-\lambda \,\operatorname {grad} T$

where λ is $\lambda$ the thermal conductivity.

In fluid mechanics, a potential flow is a flow in which the velocity is a gradient of a potential field, see velocity potential.

Image processing

→ Main article: Edge detection

One problem in image processing is to detect contiguous areas in an image. Since an image contains discrete values, filters like the Sobel operator are used to obtain a gradient field of the image. A filter is a matrix that is used to convolve the image (see Discrete Convolution). The edges in the image are then recognizable as extreme values of the filtered image.

More applications

Just as Gauss-Newton methods are used for finding zeros of functions, the gradient method is used for multidimensional optimization problems in numerics.
A pressure gradient microphone exploits the pressure differences between spatial points.

Generalizations

Gradients of vectors and tensors

Riemannian manifolds

For a smooth function on a Riemannian manifold (M,g) the gradient of is that vector field $\nabla f$ with which for each vector field the equation

$g(\nabla f,X)=\partial _{X}f,\qquad \mathrm {d.\,h.} \quad g_{x}((\nabla f)_{x},X_{x})=(\partial _{X}f)(x),$

where $g_{x}(\cdot ,\cdot )$ the inner product of tangent vectors at defined by and ∂ $\partial _{X}f$ (often $X(f)$ called ) is that function, which gives to each point $x\in M$ the directional derivative of in direction , evaluated in , is assigned. In other words, in a map φ $\varphi$ from an open subset of to an open subset of $\mathbb {R} ^{n}$ is $(\partial _{X}f)(x)$ given by:

$\sum _{j=1}^{n}X^{j}(\varphi (x)){\frac {\partial }{\partial x_{j}}}(f\circ \varphi ^{-1}){\Big |}_{\varphi (x)},$

where $X^{j}$ is the component of in these coordinates.

In local coordinates the gradient has the form

$\nabla f=g^{ik}{\frac {\partial f}{\partial x^{k}}}{\frac {\partial }{\partial x^{i}}}.$

Analogous to the case $M=\mathbb {R} ^{n}$ one has the relation of the gradient with the outer derivative by means of

$(\partial _{X}f)(x)=df_{x}(X_{x})\ .$

More precisely, $\nabla f$ is that of 1-form $\mathrm {d} f$ under the musical isomorphism ("sharp") defined by means of the metric

$\sharp =\sharp ^{g}\colon T^{*}M\to TM$

corresponding vector field. The relation between outer derivative and gradient for functions on the $\mathbb {R} ^{n}$ is the special case for the flat metric given by the Euclidean scalar product.