Golden ratio

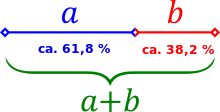
The golden ratio (Latin sectio aurea, proportio divina) is the division of a distance or other quantity in which the ratio of the whole to its larger part (also called the major) is equal to the ratio of the larger to the smaller part (the minor). Thus, with as the major and as the minor:

${\frac {a+b}{a}}={\frac {a}{b}}$ or ${\frac {a}{a+b}}={\frac {b}{a}}$

The division ratio of the golden section calculated as a number by dividing these quantities is an irrational number, i.e. a number that cannot be represented as a fraction of whole numbers. This number is also called the golden ratio or the golden number. The mathematical symbol for this number is usually the Greek letter Phi ( $\Phi$ , ϕ $\phi$ or φ $\varphi$ , present-day pronunciation [fi:]), more rarely also Tau ( $\mathrm{T}$ , τ {\displaystyle $\tau$ ) or used:

$\Phi ={\frac {a}{b}}={\frac {a+b}{a}}={\frac {1+{\sqrt {5}}}{2}}\approx 1{,}6180339887$

Knowledge of the golden section has been documented in mathematical literature since the time of Greek antiquity (Euclid of Alexandria). In the late Middle Ages (Campanus of Novara) and especially in the Renaissance (Luca Pacioli, Johannes Kepler), it was also placed in philosophical and theological contexts. Since the 19th century, it has been valued first in aesthetic theory (Adolf Zeising) and then also in artistic, architectural and craft practice as an ideal principle of aesthetic proportioning. However, there is no empirical evidence of a special aesthetic effect emanating from proportions of the golden ratio. Even the founder of empirical aesthetics, Gustav Theodor Fechner, stated on the basis of his own experiments: "Accordingly, I cannot but find the aesthetic value of the golden section ... overestimated." The historical question of whether the golden section already played a role in the proportioning of works of art and buildings of older epochs is also disputed.

The relationship of the golden section is not only important in mathematics, art or architecture, but is also found in nature, for example in the arrangement of leaves and in the inflorescences of some plants.

Proportions in the golden section of a line: $\Phi ={\frac {a}{b}}={\frac {a+b}{a}}$

Geometric statements

Construction method

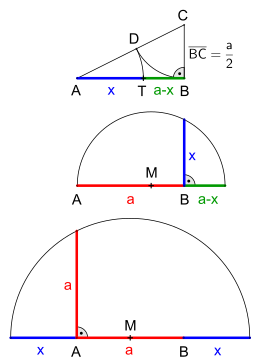
According to the postulates of Euclid, only those methods are accepted as construction methods that are limited to the use of compass and ruler (without scale). For the division of a line in the ratio of the golden section, there is an abundance of such methods, of which only a few are mentioned below as examples. A distinction is made between inner and outer division. In the case of the outer division, the point lying on the outside in the extension of the original line is sought, which makes the existing line a (larger) part of the golden section. The golden section is a special case of the harmonic division. Two modern constructions found by artists are also listed below.

Inner division

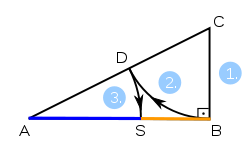
Klassische innere Teilung

Classic method with internal division, popular for its simplicity:

Establish a perpendicular of half the length of AB with end point C on the line AB at point B.
The circle around C with radius CB intersects the link AC at point D.
The circle around A with radius AD divides the distance AB at point S in the ratio of the golden section.

Innere Teilung: Verfahren nach Euklid

Inner division according to Euclid:

Goldener Schnitt, innere Teilung nach Euklid

Johann Friedrich Lorenz described in 1781 in his book Euclid's Elements the following task of Euclid: "To intersect a given straight line, AB, in such a way that the rectangle of the whole and one of the sections is equal to the square of the other section".

The result of the animation opposite shows that the line ${\overline {AB}}$ is divided in a ratio that is now known as the golden section with internal division.

As a representation of this process, a simplified construction, see left picture, has proven to be useful:

Establish a perpendicular of half the length of AB with end point C on the line AB at point A.
The circle around C with radius CB intersects the extension of AC at point D.
The circle around A with radius AD divides the distance AB at point S in the ratio of the golden section.

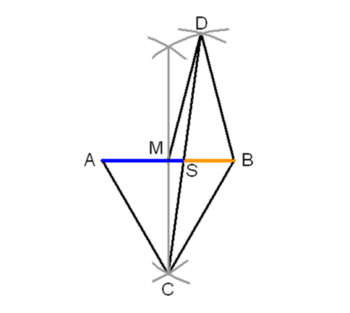
Konstruktion nach Hofstetter

Construction after the Austrian artist Kurt Hofstetter, which he published in Forum Geometricorum in 2005:

Bisect the distance AB in M by line symmetrals of radius AB, constructing an equilateral triangle ABC with side length AB and C below AB.
Construct an isosceles triangle MBD with side length AB over the base line MB
The line CD divides the line AB at point S in the ratio of the golden section.

Outer division

Äußere Teilung

Classic procedure with external division:

Establish a perpendicular of length AS with endpoint C on the line AS at point S.
Construct the centre M of the line AS.
The circle around M with radius MC intersects the extension of AS at point B. S divides AB in the ratio of the golden section.

This method is used, for example, for the construction of the pentagon with a given side length.

Konstruktion nach Odom

Construction after the American artist George Odom, who discovered it in 1982:

Construct an equilateral triangle.
Construct the circumcircle, i.e. the circle that passes through all the corners of the triangle.
Halve two sides of the triangle at points A and S.
The extension of AS intersects the circle at point B. S divides AB in the ratio of the golden section.

Instead of always having to construct anew, a Golden Compass - a reduction compass set to the Golden Ratio - was used by artists and craftsmen in the 19th century. In the carpentry trade in particular, a similar instrument in the form of a stork's beak was used.

The Golden Section in the Pentagon and the Pentagram

The regular pentagon and the pentagram each form a basic figure in which the relationship of the golden ratio occurs repeatedly. The side of a regular pentagon, for example, is in the golden ratio to its diagonals. The diagonals among themselves in turn also divide in the golden ratio, i.e., ${\overline {AD}}$ behaves to $\overline{BD}$ as $\overline{BD}$ to $\overline{CD}$ . The proof of this uses the similarity of suitably chosen triangles.

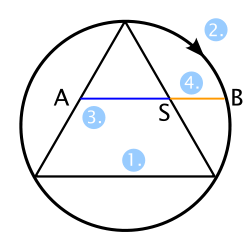
The pentagram, one of the oldest magical symbols in cultural history, has a particularly close relationship to the golden section. There is a partner for every line and part of a line in the pentagram that is related to it in the relationship of the golden section. In the illustration, all three possible pairs of routes are marked in blue (longer route) and orange (shorter route). They can be created one after the other using the continuous division method described above. In principle, this can be continued into the reduced pentagram, which could be drawn into the inner pentagon, and thus into all the others. If the two distances were in a ratio of whole numbers, this procedure of continued subtraction would have to result in zero at some point and thus break off. The observation of the pentagram, however, clearly shows that this is not the case. A further development of this geometry is found in the Penrose parquetry.

For the proof that it is the golden section, note that in addition to the many lines that are of equal length for obvious reasons of symmetry, ${\overline {\mathrm {CD} }}={\overline {\mathrm {CC'} }}$ holds. The reason is that the triangle has $DCC^{\prime }$ two equal angles, as can $CC^{\prime }$ be seen by parallel translation of the line , and is therefore isosceles. According to the ray theorem:

${\frac {\overline {\mathrm {AB} }}{\overline {\mathrm {BB'} }}}={\frac {\overline {\mathrm {AC} }}{\overline {\mathrm {CC'} }}}$

If ${\overline {\mathrm {AC} }}={\overline {\mathrm {AB} }}+{\overline {\mathrm {BC} }}$ and observing the equality of the parts occurring, exactly the above definition equation for the golden section is obtained.

Golden Rectangle and Golden Triangle

A rectangle whose aspect ratio corresponds to the golden section is called a golden rectangle, and likewise an isosceles triangle in which two sides are in this ratio is called a golden triangle.

For comparison of rectangular proportions, see section Comparison with other prominent aspect ratios.
A golden triangle is the content of the method inner division in the section Construction method.

Golden corner

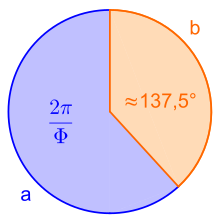
Blattstand einer Pflanze mit einem Blattabstand nach dem Goldenen Winkel

The golden angle is obtained when the solid angle is divided in the golden section. This leads to the obtuse angle ${\tfrac {2\pi }{\Phi }}\approx 3{,}88\approx 222{,}5^{\circ }.$ Usually, however, its complement to the solid angle, $2\pi -{\tfrac {2\pi }{\Phi }}\approx 2{,}40\approx 137{,}5^{\circ }$ is called the golden angle. This is justified by the fact that rotations by $\pm 2\pi$ not matter and the sign only denotes the direction of rotation of the angle.

By repeated rotation around the golden angle, new positions are created again and again, for example for the leaf beginnings in the picture. As with any irrational number, exact overlaps will never occur. Because the golden number is the most "irrational" number in the sense described below, the overlap of the leaves, which impedes photosynthesis, is minimised in total.

The first positions divide the circle into sections. These have at most three different angles. In the case of a Fibonacci number $n=f_{k}$ only two angles ${\tfrac {2\pi }{\Phi ^{k-1}}},{\tfrac {2\pi }{\Phi ^{k}}}$ occur. For $f_{k}<n<f_{k+1}$ angle 2 π Φ k +

If we look at the decreasing divisions of the circle for increasing , the (n+1) -th position always divides one of the remaining largest sections, and always the one that arose first in the course of the divisions, i.e. the "oldest" section. This division takes place in the golden ratio, so that, seen clockwise, an angle ${\tfrac {2\pi }{\Phi ^{l}}}$ with even $l\pm 1$ lies before an angle ${\tfrac {2\pi }{\Phi ^{l\pm 1}}}$ with odd

If we w_k denote the section with angle ${\tfrac {2\pi }{\Phi ^{k}}}$ with , we get successively the circle decompositions $w_{0},$ $w_{2}w_{1},$ $w_{2}w_{2}w_{3},$ $w_{4}w_{3}w_{2}w_{3},$ $w_{4}w_{3}w_{4}w_{3}w_{3},$ $w_{4}w_{3}w_{4}w_{3}w_{4}w_{5},$ $w_{4}w_{4}w_{5}w_{4}w_{3}w_{4}w_{5},$ $w_{4}w_{4}w_{5}w_{4}w_{4}w_{5}w_{4}w_{5},$ $w_{6}w_{5}w_{4}w_{5}w_{4}w_{4}w_{5}w_{4}w_{5},$ $w_{6}w_{5}w_{4}w_{5}w_{6}w_{5}w_{4}w_{5}w_{4}w_{5}$ etc.

Golden spiral

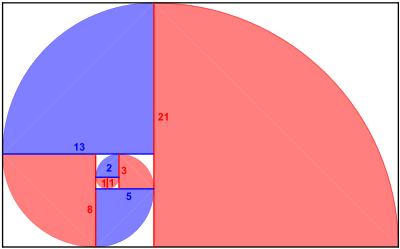
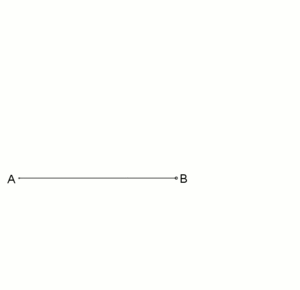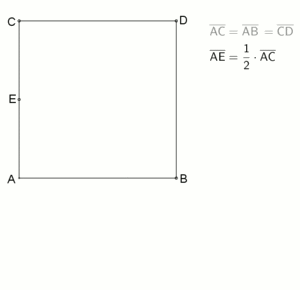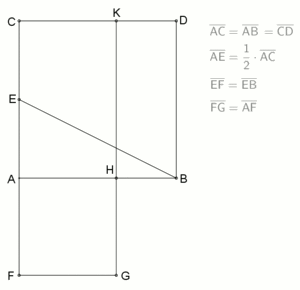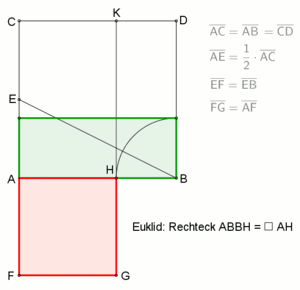
The golden spiral is a special case of the logarithmic spiral. This spiral can be constructed by recursively dividing a golden rectangle into a square and another, smaller golden rectangle (see picture opposite). It is often approximated by a sequence of quarter circles. Its radius changes by a factor $\Phi$ each 90° rotation.

It applies

$\textstyle r(\theta )=ae^{k\theta }=a\Phi ^{\frac {2\theta }{\pi }}$

with the slope $\textstyle k=\pm {\frac {\ln {\Phi }}{\alpha _{\llcorner }}}$ where α $\alpha _{\llcorner }$ the numerical value for the right angle, i.e. 90° or ${\tfrac {\pi }{2}}$ , so $\textstyle k={\frac {2\ln(\Phi )}{\pi }}$ with the golden number $\textstyle \Phi ={\frac {{\sqrt {5}}+1}{2}}$ .

Consequently, the following applies to the slope:

$\textstyle |k|\approx 0{,}005346798/{}^{\circ }\approx 0{,}30634896/\mathrm {rad}$

The golden spiral is distinguished among the logarithmic spirals by the following property. Let $P_{1},P_{2},P_{3},P_{4}$ be four successive intersections on the spiral with a straight line through the centre. Then the two pairs of points $P_{1},P_{4}$ and are P_2,P_3 harmonically conjugate, i.e., for their double ratio applies

$(P_{\theta },P_{\theta +3\pi };P_{\theta +\pi },P_{\theta +2\pi })={\frac {(-\Phi ^{6}-\Phi ^{4})(-\Phi ^{2}-1)}{(-\Phi ^{6}+\Phi ^{2})(\Phi ^{4}-1)}}={\frac {-\Phi ^{2}}{(-\Phi ^{2}+1)^{2}}}=-1.$

Golden section in the icosahedron

The twelve corners of the icosahedron form the corners of three rectangles of the same size standing vertically on top of each other with a common centre and with the aspect ratios of the golden section. This arrangement of the three rectangles is also called the golden section chair. Because the icosahedron is dual to the pentagon dodecahedron, the twelve centres of the pentagons also form the corners of a golden section chair.

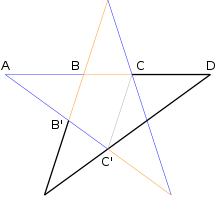
Pentagram

Golden spiral approximated by quarter circles. The ratio of the radii of the circle sectors corresponds to the Fibonacci sequence $1,1,2,3,5,8,13,21,\ldots$

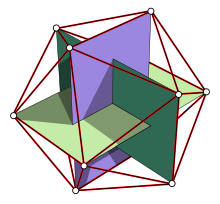
Three Golden Rectangles in the Icosahedron

The golden angle ( $\approx 137{,}5^{\circ }$ ) is the circular angle of the smaller arc if it a+b forms a circle of circumference with the larger arc and the ratio corresponds to the golden section.

Mathematical properties

Derivation of the numerical value

Algebraic

The definition given in the introduction

${\frac {a}{b}}={\frac {a+b}{a}}$

reads with the right side dissolved and after conversion

${\frac {a}{b}}-1-{\frac {b}{a}}=0$

respectively with ${\tfrac {a}{b}}=\Phi$ follows:

$\Phi -1-{\frac {1}{\Phi }}=0$

Multiplication by $\Phi$ gives the quadratic equation

$\Phi ^{2}-\Phi -1=0$

with the two solutions ${\tfrac {1+{\sqrt {5}}}{2}}=1{,}618\ldots$ and ${\tfrac {1-{\sqrt {5}}}{2}}=-0{,}618\ldots$ which can be obtained, for example, by applying the midnight formula or also by quadratic addition.

Since of these two values only the positive one can be considered for the golden number, it follows that

$\Phi ={\frac {1+{\sqrt {5}}}{2}}=1{,}618\ldots$

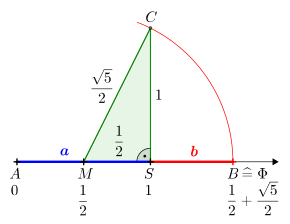
Geometric

The approach is the definition given in the introduction

$\Phi ={\frac {a}{b}}={\frac {a+b}{a}}$

with a major a=1 .

On a number line, first the numerical value designated $0$ as point and then the major plotted as numerical value resulting in the intersection point . After establishing the perpendicular on the line ${\overline {AS}}$ in line ${\overline {AS}}$ onto the perpendicular from the point intersection If we now halve ${\overline {AS}}$ in this produces the numerical value ${\tfrac {1}{2}}.$ The points $M,S$ and are vertices of the right triangle with cathets ${\overline {MS}}={\tfrac {1}{2}}$ and ${\overline {SC}}=1.$

With the help of the Pythagorean theorem

${\overline {MC}}^{2}=\left({\frac {1}{2}}\right)^{2}+1^{2}={\frac {5}{4}}$

thus obtains the hypotenuse ${\overline {MC}}={\frac {\sqrt {5}}{2}}.$

Finally, an arc is required around (numerical value ${\tfrac {1}{2}}$ ) with radius ${\tfrac {\sqrt {5}}{2}},$ which intersects the number line in ${\overline {SB}}$ shows the minor as a line and ${\tfrac {1}{2}}+{\tfrac {\sqrt {5}}{2}}$ gives the numerical value

The numerical value of $\Phi$ can thus be read directly on the number line:

${\overline {AB}}=a+b={\frac {1}{2}}+{\frac {\sqrt {5}}{2}}\;{\mathrel {\widehat {=}}}\;\Phi$

Summarised it also results in

$\Phi ={\frac {1+{\sqrt {5}}}{2}}=1{,}618\ldots$

The Golden Sequence of Numbers

Golden number sequence for a0 = 1
	$a_{z}=\Phi ^{z}\cdot a_{0}$
4	≈ 6,854	$\Phi ^{4}=3\cdot \Phi +2$
3	≈ 4,236	$\Phi ^{3}=2\cdot \Phi +1$
2	≈ 2,618	$\Phi ^{2}=\Phi +1$
1	≈ 1,618	$\Phi$
0	= 1,000	$\Phi ^{0}=1$
−1	≈ 0,618	$\Phi ^{-1}=\Phi -1$
−2	≈ 0,382	$\Phi ^{-2}=-\Phi +2$
−3	≈ 0,236	$\Phi ^{-3}=2\cdot \Phi -3$
−4	≈ 0,146	$\Phi ^{-4}=-3\cdot \Phi +5$

For a given number $a_{0}$ sequence $a_{z}:=\Phi ^{z}\cdot a_{0}$ for $z\in \mathbb {Z}$ construct. This sequence has the property that each three consecutive links $(a_{z-1},a_{z},a_{z+1})$ form a golden section, that is, it holds

${\frac {a_{z}}{a_{z-1}}}={\frac {a_{z+1}}{a_{z}}}$ and $a_{z+1}=a_{z}+a_{z-1}$ for all $z\in \mathbb {Z} .$

This sequence plays an important role in the theory of proportions in art and architecture, because for a given length $a_{0}$ further lengths can be created that appear harmonious. In this way, even objects of very different dimensions, such as window and room widths, can be related by means of the golden section and entire series of mutually harmonious dimensions can be created.

It is worth mentioning that for a_0 = 1 the decimal places for $a_{{-1}}$ , $a_{1}$ and $a_{2}$ not differ because they are positive and the difference between them is an integer. Thus the decimal number here is always x,618,033,988,75... with x= 0, 1, 2.

Connection with the Fibonacci numbers

Ratios of successiveFibonacci numbers
$f_{n}$	$f_{{n+1}}$	${\frac {f_{n+1}}{f_{n}}}$	Deviation to $\Phi$ in %.
01	01	= 1,0000	−38,0000
01	02	= 2,0000	+23,0000
02	03	= 1,5000	−7,300
03	05	≈ 1,6667	+3,000
05	08	= 1,6000	−1,100
08	13	= 1,6250	+0,430
13	21	≈ 1,6154	−0,160
21	34	≈ 1,6190	+0,063
34	55	≈ 1,6176	−0,024
55	89	≈ 1,6182	0+0,0091
89	144	≈ 1,6180	0−0,0035
144	233	≈ 1,6181	0+0,0013

Closely related to the golden section is the infinite sequence of Fibonacci numbers (see below the sections on the Middle Ages and the Renaissance):

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 …

The next number in this sequence is obtained as the sum of the two preceding numbers. The ratio of two consecutive numbers in the Fibonacci sequence tends towards the golden ratio (see table). The recursive formation law $f_{n+1}=f_{n}+f_{n-1}$ means namely

${\frac {f_{n+1}}{f_{n}}}={\frac {f_{n}+f_{n-1}}{f_{n}}}=1+{\frac {f_{n-1}}{f_{n}}}.$

Provided that this ratio $\Phi$ converges towards a limit , the following must apply to it

$\Phi =1+{\frac {1}{\Phi }}.$

This reasoning also applies to generalised Fibonacci sequences with any two initial members.

The members of the Fibonacci sequence $f_{n}$ for all $n\in \mathbb {N}$ calculated via Binet's formula:

$f_{n}={\frac {1}{\sqrt {5}}}(\Phi ^{n}-{\bar {\Phi }}^{n})$

where ${\bar {\Phi }}=1-\Phi =-{\frac {1}{\Phi }}={\tfrac {1-{\sqrt {5}}}{2}}$

This formula yields the correct initial values $f_{0}=0$ and $f_{1}=1$ and satisfies the recursive equation $f_{n+1}=f_{n}+f_{n-1}$ for all with $n\geq 1$ .

Approximation properties of the golden number

As indicated above, the golden number $\Phi$ an irrational number, i.e. it cannot be represented as a fraction of two integers. It is sometimes called the "most irrational" of all numbers because it can be approximated (in a special number-theoretical sense) particularly badly by rational numbers (Diophantine approximation). This will be $\pi$ illustrated in the following by a comparison with the likewise irrational circular number π latter is much better approximable than $\Phi$ for example, π {\displaystyle $\pi$ approximated by the fraction ${\tfrac {22}{7}}$ with a deviation of only about 0.00126. Such a small error would generally only be expected with a much larger denominator.

The golden number can be constructed directly from the requirement of the worst possible approximability by rational numbers. To understand this, consider the following procedure for approximating arbitrary numbers by a fraction using the example of the number π $\pi$ First, this number is decomposed into its integer part and a remainder smaller than : $\pi =3+{\text{Rest}}$ . The inverse of this remainder is a number greater than It can therefore again be decomposed into an integer part and a remainder smaller than : π $\pi =3+{\tfrac {1}{7+{\text{Rest}}}}$ . If the same is done with this remainder and all the following ones, then the infinite continued fraction development of the number π follows. $\pi$

$\pi =3+{\cfrac {1}{7+{\cfrac {1}{15+{\cfrac {1}{1+\dotsb }}}}}}$

If this continued fraction evolution is terminated after finitely many steps, then for π $\pi$ the known approximations , ${\tfrac {22}{7}}$ , ${\tfrac {333}{106}}$ , ${\tfrac {355}{113}}$ , ... which rapidly $\pi$ tend towards π For every single one of these fractions, it holds that there is no fraction with a denominator of at most equal size that $\pi$ better approximates π This is true in general:

If the continued fraction expansion of an irrational number is terminated at any point, then a rational number results. p/q which optimally approximates among all rational numbers with denominator ≤ $\leq q$ .

In the continued fraction above, an integer appears before each plus sign. The larger this number, the smaller the fraction in whose denominator it appears, and therefore the smaller the error that occurs when the infinite continued fraction is terminated before this fraction. The largest number in the continued fraction section above is . This is why ${\tfrac {22}{7}}$ is such a good approximation for π $\pi$

Reversing this argumentation, it now follows that the approximation is particularly bad if the number before the plus sign is particularly small. The smallest permissible number there is . The continued fraction, which contains only ones, can therefore be approximated particularly badly by rational numbers and is in this sense the "most irrational of all numbers".

For the golden number, however, $\Phi =1+{\tfrac {1}{\Phi }}$ (see above), from which, by repeated application, we get

$\Phi =1+{\frac {1}{\Phi }}=1+{\frac {1}{1+{\frac {1}{\Phi }}}}=\dotsb =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {\cdots }{\dotsb +{\cfrac {1}{\Phi }}}}}}}}}}$

Since the continued fraction expansion of the golden number $\Phi$ contains only ones, it belongs to the numbers that are particularly difficult to approximate rationally. If its continued fraction development breaks off at any point, a fraction of two consecutive Fibonacci numbers is always obtained.

Another curious designation is the following: In the theory of dynamical systems, numbers whose infinite continued fraction representation contains only ones from any point on are called "noble numbers". Since the golden number has only ones in its continued fraction, it can (jokingly) be called the "noblest of all numbers".

From an algebraic-number-theoretical point of view

The golden section is an algebraic number as the zero of the polynomial $X^{2}-X-1$ Because the polynomial is normalised and all coefficients are integers, the golden section is even whole. Let $K:=\mathbb {Q} (\Phi )=\mathbb {Q} ({\sqrt {5}})$ , then $K/\mathbb {Q}$ is a body extension of degree 2. Thus a square number body. It is the real quadratic number body of smallest discriminant, namely 5 (the real quadratic number body with next larger discriminant is $\mathbb {Q} ({\sqrt {2}})$ with discriminant 8). Let ${\mathcal {O}}_{K}$ be the associated integer ring. Because $\Phi$ is integer, $\Phi \in {\mathcal {O}}_{K}$ , but more than that: because of

$N_{K/\mathbb {Q} }(\Phi )=\Phi \Phi '={\frac {1+{\sqrt {5}}}{2}}\cdot {\frac {1-{\sqrt {5}}}{2}}={\frac {1-5}{4}}=-1\in \mathbb {Z} ^{\times }$

is the golden section even unit of the integer ring ${\mathcal {O}}_{K}$ . Its multiplicative inverse is $-\Phi '={\tfrac {{\sqrt {5}}-1}{2}}=\Phi -1$ . This can also be shown algebraically just by knowing the minimal polynomial $X^{2}-X-1$

$\Phi (\Phi -1)=\Phi ^{2}-\Phi =\Phi ^{2}-\Phi -(\Phi ^{2}-\Phi -1)=1.$

However, the golden section is not only a unit of the holistic ring ${\mathcal {O}}_{K}$ but even a fundamental unit of the holistic ring. That is, each element of ${\mathcal {O}}_{K}^{\times }$ is of the form $\pm \Phi ^{n}$ with $n\in \mathbb {\mathbb {Z} }$ . Moreover, $1,\Phi \in {\mathcal {O}}_{K}$ form a $\mathbb {Z}$ -basis of ${\mathcal {O}}_{K}$ . That is, each element of ${\mathcal {O}}_{K}$ be uniquely written as $a+b\Phi$ with $a,b\in {\mathbb Z}$ write. A simple consequence of the next paragraph is that also $1,\Phi ^{2}\in {\mathcal {O}}_{K}$ a $\mathbb {Z}$ -base of ${\mathcal {O}}_{K}$ . Here $\Phi ^{2}={\tfrac {3+{\sqrt {5}}}{2}}$ .

The whole boundary points of the convex hull of ${\mathcal {O}}_{K}^{+}:=\{x\in {\mathcal {O}}_{K}\mid x\gg 0\}$ , which are important, for example, for the desingularisation of peaks of Hilbert modular surfaces, are $\Phi$ given by the even powers of The fact that these boundary points all ${\mathcal {O}}_{K}^{\times }$ lie in i.e. are all units, is equivalent to the singularity of the rational curves in the Hilbert modular surface associated with the body living "infinitely" above it in the resolution of the top.

Other mathematical properties

From following infinite chain root can be derived $\Phi ^{2}=1+\Phi$ :

$\Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dotsb }}}}}}}}$

The square $\Phi ^{2}=\Phi +1$ and any higher integer power of $\Phi$ represented as the sum of an integer multiple of $\Phi$ and an integer multiple of 1. The fundamental significance of the golden section for quasiperiodic lattices is based on this property (see quasicrystal).
More precisely, $\Phi ^{n}=\Phi ^{n-1}+\Phi ^{n-2}=f_{n-1}+f_{n}\cdot \Phi =f_{n+1}+f_{n}\cdot {\tfrac {1}{\Phi }}$ (where $f_{n}$ the th Fibonacci number).

A brief proof of this relationship is provided by the direct representation of the Fibonacci numbers using $\Phi ^{-1}=-\Psi$ and $\Psi ^{-1}=-\Phi$ :

$(\Phi -\Psi )(f_{n-1}+f_{n}\cdot \Phi )=\Phi ^{n-1}-\Psi ^{n-1}+\Phi ^{n+1}-\Psi ^{n}\Phi =-\Psi \Phi ^{n}+\Phi \Psi ^{n}+\Phi ^{n+1}-\Phi \Psi ^{n}=(\Phi -\Psi )\Phi ^{n}$ , since falls out $\pm \Phi \Psi ^{n}$

the first assertion results after division by $(\Phi -\Psi )\neq 0$ . - In the analogous proof of the second assertion $\pm \Psi ^{n+1}$ falls out.

From trigonometry follows, among other things

$\Phi =2\cos \left({\frac {\pi }{5}}\right)=2\sin \left({\frac {3\pi }{10}}\right)$

and

${\frac {1}{\Phi }}=2\sin \left({\frac {\pi }{10}}\right)=2\cos \left({\frac {2\pi }{5}}\right).$

${\tfrac {\pi }{5}}$ is the full acute angle and ${\tfrac {3\pi }{10}}$ half the obtuse exterior angle of the pentagram. Occasionally the role of the golden section for the pentagon is described as comparably important as that of the circle number π $\pi$ for the circle.

The golden section can also be expressed with the help of the Eulerian number and the hyperbolic areasinus function:

$\Phi ^{\pm 1}=e^{\operatorname {arsinh} \left(\pm {\frac {1}{2}}\right)}$

Substituting $q={\tfrac {1}{\Phi }}$ into the geometric series formula ∑ k = $\textstyle \sum _{k=1}^{\infty }q^{k}={\frac {q}{1-q}}$

$\Phi =\sum _{k=1}^{\infty }{\frac {1}{\Phi ^{k}}}$ , because $\sum _{k=1}^{\infty }{\frac {1}{\Phi ^{k}}}={\frac {\frac {1}{\Phi }}{1-{\frac {1}{\Phi }}}}={\frac {1}{\Phi -1}}=\Phi$ .

Application of the binomial theorem to the relationship $\textstyle 1^{n}=({\frac {1}{\Phi }}+{\frac {1}{\Phi ^{2}}})^{n}=({\frac {1}{\Phi ^{2}}}+{\frac {1}{\Phi }})^{n}$ gives:

$1=\sum _{k=0}^{n}{\binom {n}{k}}{\frac {1}{\Phi ^{n+k}}}=\sum _{k=0}^{n}{\binom {n}{k}}{\frac {1}{\Phi ^{2n-k}}}$ or: $\Phi ^{n}=\sum _{k=0}^{n}{\binom {n}{k}}{\frac {1}{\Phi ^{k}}}$ .

Geometric derivation
Major a=1 yields the golden number $\Phi ={\tfrac {1+{\sqrt {5}}}{2}}$ .
Animation

Generalisation of the Golden Section

Geometric means

If the line ${\overline {AB}}$ is interpreted in its length |AB| as a real number and the division by the golden section at the point into the two subsections $\overline {AT}$ and ${\overline {BT}}$ as a decomposition of this number into two summands and a-x , then is the geometric mean of the numbers and a-x . This follows from the general definition of the geometric mean ${\bar {x}}_{\text{geom}}={\sqrt[{n}]{x_{1}\cdot x_{2}\dotsm x_{n}}}$ , here: $x={\sqrt[{2}]{a(a-x)}}$ . Furthermore, it follows immediately that is again the geometric mean of and a+x

For any real , a mathematical sequence can therefore be specified in ascending as well as descending order. The ascending as well as the descending sequence is defined recursively in each case.

For the ascending sequence: $a_{i+1}=a_{i}+{\tfrac {1}{2}}(1+{\sqrt {5}})a_{i}$ with the starting point $a_{0}=a$

For the descending sequence: $a_{i+1}=a_{i}-{\tfrac {1}{2}}(1+{\sqrt {5}})a_{i}$ with the starting point $a_{0}=a$

Continuous division

The geometric generalisation of the golden section by its multiple application is the continuous division of a line ${\overline {AB}}$ . Here the line ${\overline {AB}}$ first divided into a smaller line ${\overline {AA'}}$ and a larger ${\overline {A'B}}$ The line ${\overline {A'B}}$ (i.e. the larger of the resulting line segments) is now subjected to another golden section, leaving ${\overline {A''B}}$ as the (new) larger line segment and ${\overline {A'A''}}$ as the smaller one. This step can now be repeated infinitely often, since due to the mathematical properties of the golden section, despite the progressive division, there will be no point } $A^{{(n)}}$ that coincides with the original point

However, this general procedure can also be achieved by subtracting the line ${\overline {AA'}}$ the point after the construction of The point obtained A'' is the same as the point just described in the (general) decomposition A'' .

This sequence of steps is called a continuous division of a line ${\overline {AB}}$

Analytically, the continuous division as a generalisation of the golden section is an example of self-similarity: If the resulting lengths of the lines are interpreted as real numbers, the following applies: If the shorter of the two lines is subtracted from the longer one, an even shorter line a-b to which the middle distance again in the ratio of the golden section, i.e.

${\frac {b}{a-b}}={\frac {a}{b}}.$

This statement is again analytically identical to the descending geometric sequence of the previous section. Consequently, the same statement applies to the extension of a given distance, it leads to the ascending geometric sequence.

From this statement, however, the following also applies: A rectangle with the sides and corresponds exactly to the golden section if this is also the case for the rectangle with the sides a+b and A golden rectangle can therefore always be decomposed into a smaller golden rectangle and a square. This generalisation is in turn the basis for the construction of the (infinite) Golden Spiral, as described above.

Geometric mean:
divides the line ${\overline {AB}}$ in the ratio of the golden section.
$x={\sqrt {a(a-x)}}$
$a={\sqrt {x(a+x)}}$

Occurrence in nature

Biology

The most spectacular example of ratios of the golden section in nature is found in the arrangement of leaves (phyllotaxy) and in inflorescences of some plants. In these plants, the angle between two successive leaves divides the full circle of 360° in the ratio of the golden section when the two leaf bases are brought into alignment by a parallel displacement of one of the leaves along the plant axis. This is the golden angle of about 137.5°.

The resulting structures are also called self-similar: In this way, a pattern of a lower structural level is found in higher levels. Examples are the sunflower, cabbages, pine needles on young branches, cones, agaves, many palm and yucca species, and the petals of the rose, to name but a few.

The cause is the effort of these plants to keep their leaves at a distance. It is assumed that they produce a special growth inhibitor (inhibitor) at each leaf attachment for this purpose, which diffuses in the plant stem - mainly upwards, but to a lesser extent also in a lateral direction. In the process, certain concentration gradients form in different directions. The next leaf develops at a point on the circumference where the concentration is minimal. In the process, a certain angle to the predecessor is established. If this angle were to divide the full circle in the ratio of a rational number ${\tfrac {m}{n}}$ , then this leaf would grow in exactly the same direction as the one leaves before. However, the contribution of this leaf to the concentration of the inhibitor is just maximal at this point. Therefore, an angle with a ratio that avoids all rational numbers is set up. However, the number is now just the golden number (see above). Since no such inhibitor could be isolated so far, other hypotheses are also being discussed, such as the control of these processes in an analogous way by concentration distributions of nutrients.

The benefit for the plant could be that sunlight (or water and air) falling from above is used optimally in this way, a conjecture already expressed by Leonardo da Vinci, or also in the more efficient transport of the carbohydrates produced by photosynthesis downwards in the phloem part of the vascular bundles. The roots of plants show the golden angle less clearly. In other plants, on the other hand, leaf spirals appear with other angles. For example, in some species of cacti an angle of 99.5° is observed, which corresponds to the variant of the Fibonacci sequence 1, 3, 4, 7, 11, .... In computer simulations of plant growth, these different behaviours can be provoked by appropriate choice of diffusion coefficients of the inhibitor.

In many plants organised according to the golden section, so-called Fibonacci spirals form in this context. Spirals of this type are particularly easy to recognise when the leaf spacing is particularly small compared to the circumference of the plant axis. They are not formed by successive leaves, but by those at a distance where is a Fibonacci number. Such leaves are in close proximity because times the golden angle }}\approx $2\pi -{\tfrac {2\pi }{\Phi }}\approx 137{,}5^{\circ }$ is approximately a multiple of 360° because of

$n\cdot 360^{\circ }\cdot \left(1-{\frac {1}{\Phi }}\right)\approx n\cdot {\frac {m}{n}}\cdot 360^{\circ }=m\cdot 360^{\circ },$

where is the next smaller Fibonacci number to Since each of the leaves between these two belongs to a different spiral, spirals are seen. If is ${\tfrac {n}{m}}$ greater than $\Phi$ then the ratio of the two nearest Fibonacci numbers is smaller and vice versa. Therefore, spirals to successive Fibonacci numbers can be seen in both directions. The sense of rotation of the two types of spirals is left to chance, so that both possibilities occur with equal frequency.

Fibonacci spirals (which are in turn associated with the golden section) are particularly impressive in inflorescences, as in sunflowers. There, flowers that later develop into fruits sit close together on the strongly compressed, disc-shaped inflorescence axis, whereby each individual flower can be assigned to its own circle around the centre of the inflorescence. Consecutive fruits in terms of growth are therefore spatially far apart, while direct neighbours again have a distance corresponding to a Fibonacci number. In the outer area of sunflowers, 34 and 55 spirals are counted, in larger specimens 55 and 89 or even 89 and 144. The deviation from the mathematical golden angle, which is not exceeded in this case, is less than 0.01 %.

The golden ratio can also be seen in radially symmetrical five-petalled flowers such as the bellflower, columbine and (wild) hedge rose. The distance between the tips of petals of nearest neighbours and those of the next but one is in proportion, as is usual with the regular pentagon. This also applies to starfish and other animals with pentagonal symmetry.

In addition, the golden section is also assumed in the ratio of the lengths of successive stem sections of some plants, as in the case of the poplar. In the ivy leaf, too, the leaf axes a and b (see illustration) are approximately in the ratio of the golden section. However, these examples are disputed.

Even in the 19th century, the view was widespread that the Golden Section was a divine law of nature and was also realised in many ways in the proportions of the human body. Adolf Zeising, for example, in his book on the proportions of the human body, assumed that the navel divided the height of the body in the ratio of the golden section, and the lower section was in turn divided in this way by the knee. Furthermore, the ratios of adjacent parts of the limbs, such as the upper and lower arm and the phalanges, seem to be approximately in this proportion. However, a close examination reveals scattering of the ratios in the 20 % range. Often the definition of how the length of a body part is to be exactly determined contains a certain amount of arbitrariness. Furthermore, this thesis still lacks a scientific basis. Therefore, the view largely dominates that these observations are merely the result of targeted selection of neighbouring pairs from a set of arbitrary sizes.

Railway resonances

It has long been known that the orbital periods of some planets and moons are in ratios of small integers, such as Jupiter and Saturn with 2:5 or the Jupiter moons Io, Ganymede and Europa with 1:2:4. Such orbital resonances stabilise the orbits of the celestial bodies in the long term against minor perturbations. It was not until 1964 that it was discovered that sufficiently irrational ratios, as would exist in the case $1:\Phi$ can also have a stabilising effect. Such orbits are called KAM orbits, where the three letters stand for the names of the discoverers Andrei Kolmogorov, V. I. Arnold and Jürgen Moser.

Black holes

Contractible cosmic objects without a solid surface, such as black holes or the sun, have the paradoxical property of becoming hotter when they radiate heat (negative heat capacity) due to their self-gravity. In the case of rotating black holes, a switch from negative to positive heat capacity takes place above a critical angular momentum, whereby this tipping point depends on the mass of the black hole. In a -dimensional spacetime, a metric play, whose eigenvalues Φ {\displaystyle ${\bigl (}{\begin{smallmatrix}d-3&1\\1&0\end{smallmatrix}}{\bigr )}$ $\Phi$ 4 {\displaystyle d=4 zeros of the characteristic polynomial

$\left|{\begin{pmatrix}1-\Phi &1\\1&-\Phi \end{pmatrix}}\right|=\Phi ^{2}-\Phi -1$

result.

Crystal structures

The golden ratio also appears in the quasicrystals of solid-state physics, which were discovered by Dan Shechtman and his colleagues in 1984. These are structures with five-fold symmetry, from which, however, as Kepler already recognised, no strictly periodic crystal lattices can be built, as is usual for crystals. The surprise was correspondingly great when diffraction images with pentagonal symmetry were found in X-ray structural analyses. These quasicrystals structurally consist of two different rhombohedral basic building blocks with which the space can be filled without gaps but without global periodicity (Penrose parquetry). Both rhombohedra are composed of the same rhombic side faces, which are, however, oriented differently. The shape of these rhombuses can now be defined by the fact that their diagonals are in the ratio of the golden section. Shechtman was awarded the Nobel Prize in Chemistry in 2011 for the discovery of quasicrystals.

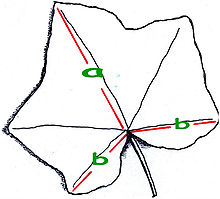
Golden section in the ivy leaf

Sunflower with 34 and 55 Fibonacci spirals

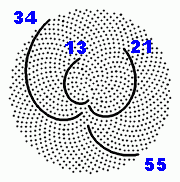
Calculated inflorescence with 1000 fruits in the Golden Angle - 13, 21, 34 and 55 Fibonacci spirals appear.

Spruce cones with 5, 8 and 13 Fibonacci spirals

Arrangement of leaves at the distance of the golden angle viewed from above. The sunlight is used optimally.

Questions and Answers

Q: What is the ratio of two numbers?

A: The ratio of two numbers is found by dividing them, so the ratio would be a/b.

Q: How can another ratio be found?

A: Another ratio can be found by adding the two numbers together and then dividing this sum by the larger number, a. This new ratio would be (a+b)/a.

Q: What is the name for when these two ratios are equal to each other?

A: When these two ratios are equal to each other, it is called the golden ratio. It is usually represented with Greek letter φ or phi.

Q: If b = 1 and a/b = φ , what does that mean for a?

A: If b = 1 and a/b = φ , then that means that a = φ as well.

Q: How can one way write this number?

A: One way to write this number is φ = 1 + 5 / 2 = 1.618...

Q: What does it mean if you subtract 1 from it or divide 1 by it?

A: If you subtract 1 from it or divide 1 by it, you will get back the same number - in other words, they will both equal the golden ratio.

Q: Is the golden ration an irrational number?

A: Yes, the golden ration is an irrational number which means that if someone tries to write it out, there will never be an end and no pattern - only starting with something like "1.6180339887..."