Gibbs free energy

This article has been entered into the quality assurance of the physics editorial team. If you are familiar with the topic, you are welcome to participate in the review and possible improvement of the article. The exchange of views on this is currently not taking place on the article discussion page, but on the physics quality assurance page.

Gibbs energy (also free enthalpy), named after Josiah Willard Gibbs, is a thermodynamic potential, i.e. a state variable in thermodynamics. It is an extensive quantity with the dimension energy. In the SI system of units, it is measured in joules. Its formula symbol is and its natural variables are the temperature, the pressure and the particle numbers $\{N_{i}\}$ .

The Gibbs energy of a system is obtained from its enthalpy by a Legendre transformation with respect to the entropy by reducing the enthalpy by the product of the absolute temperature and the entropy

$G(T,p,\{N_{i}\})=H(S,p,\{N_{i}\})-T\,S$ .

or starting from the internal energy

$G(T,p,\{N_{i}\})=U(S,V,\{N_{i}\})+p\,V-T\,S$ .

where is the volume of the system.

The molar Gibbs energy (unit: J/mol) is the Gibbs energy related to the amount of substance

$G_{\text{m}}={\frac {G}{n}}$ .

The specific Gibbs energy (unit: J/kg) is the Gibbs energy related to the mass

$g={\frac {G}{m}}$ .

The molar and specific Gibbs energies are intensive quantities: If two identical subsystems have the same molar or specific Gibbs energy, then the total system formed from them also has this molar or specific Gibbs energy.

Overview

The Gibbs energy is measured in joules, but it is not an independent form of energy, such as the kinetic energy or the internal energy contained in the system or a converted heat of reaction. It must not be added up when calculating the total energy. It is merely an abbreviation for the frequently occurring expression $U+p\,V-T\,S$ . With its help, statements can be made about the behaviour of the system, such as the direction of processes running voluntarily or the position of equilibrium states.

Gibbs energy as equilibrium criterion

A process in a given thermodynamic system runs voluntarily exactly when it is associated with an increase in the total entropy of the system and its environment. If one restricts oneself to processes that take place at a temperature and pressure kept constant, then the processes that increase the entropy of the system and its surroundings are precisely those that decrease the Gibbs energy of the system. A closed system kept at constant temperature and pressure therefore assumes as its equilibrium state that state in which its Gibbs energy has the smallest possible value. If the system is not in equilibrium, it will voluntarily (unless otherwise inhibited) move to states of lower Gibbs energy until equilibrium is reached. Since many physical and chemical processes occur at constant temperature (isothermal) and constant pressure (isobaric), the Gibbs energy provides a frequently used criterion for the direction in which the process occurs voluntarily and for the location of equilibrium.

For example, for an isothermal and isobaric chemical reaction:

If the Gibbs energy of the reaction products is smaller than the Gibbs energy of the starting materials ( $\Delta G<0$ the reaction proceeds in the direction of the products.
If the Gibbs energy of the reaction products is greater than the Gibbs energy of the starting materials ( $\Delta G>0$ then the reaction proceeds in the opposite direction.
The Gibbs energy of the mixture of starting materials and products usually depends on the mixture and therefore changes in the course of a reaction. If it passes through a minimum, i.e. when a certain mixture is reached ( $\mathrm {d} G=0$ ), then in this state the outward and the reverse reaction take place at the same rate, the reacting system has reached a chemical equilibrium.

Two phases of a substance are in equilibrium with each other if the molar (or specific) Gibbs energies of the substance are the same in both phases. If the molar Gibbs energies of the phases involved are known, it can therefore be immediately recognised whether equilibrium exists or not. Conversely, if equilibrium exists, the molar Gibbs energy of all phases is known as soon as it is known for one phase. If, for example, liquid water is in equilibrium with its vapour, then the two phases have the same molar Gibbs energy. That of the vapour can be easily calculated (considered approximately as an ideal gas), the numerical value found also applies to the liquid water. If
the phases consist of mixtures of several substances, the equilibrium criterion applies separately to each substance contained in the mixture.

Chemical potential

In a single-component system, the chemical potential is identical to the molar Gibbs energy of the system. In a multi-component system, the chemical potentials are identical to the partial molar Gibbs energies of the system.

Change in the Gibbs energy of a system

If one changes the temperature of a system at constant pressure and constant quantities of substances, the Gibbs energy of the system changes proportionally to the temperature change, the proportionality constant is the negative of the entropy of the system; if one changes the pressure under the same conditions, the Gibbs energy changes proportionally to the pressure change (proportionality constant: volume of the system).

If one changes the amount of substance of one of the substances contained in the system at constant temperature, constant pressure and constant amounts of substance of the remaining substances, the Gibbs energy of the system changes proportionally to the change in amount of substance, the constant of proportionality is the chemical potential of the substance in question under the conditions prevailing in the system.

If a certain amount of reversible physical work (other than volume change work $p\,\mathrm {d} V$ ) is performed on a closed system kept at constant temperature and pressure, the Gibbs energy of the system increases by that amount. Thus, the Gibbs energy of a system can be selectively increased by, for example, performing a known amount of lifting work or electrical work on the system. Conversely, if the system performs work (other than volume change work) under the conditions mentioned, its Gibbs energy decreases by the amount in question.

The equality of the amounts of work done and the change in Gibbs energy only applies in the case of reversible work. In the irreversible case, depending on the degree of irreversibility, the work to be done on the system is greater or the work done by the system is less than the change in Gibbs energy.
In this context, the Gibbs energy provides a measure of the "driving force" of the process, such as the "affinity" of the reactants in a chemical reaction.

As a fundamental equation

The entire thermodynamic information about the system can be derived from the Gibbs energy. However, it is a prerequisite that it is calculated as a function of the variables temperature , pressure and mole numbers $n_{i}$ the chemical components contained in the system. These are the "natural variables" of the Gibbs energy. It can also be set as a function of other variables, but then no longer contains the complete thermodynamic information.

Minimum principle of Gibbs energy

According to the Second Law of Thermodynamics, a closed system takes as its equilibrium state among the attainable states the one that has the highest entropy at the given internal energy. From this maximum principle of entropy, other, equally important extreme principles can also be derived, such as, for example, a minimum principle of internal energy: with entropy kept constant, a system takes as its state of equilibrium that state which has the lowest internal energy.

A similar minimum principle exists for the Gibbs energy: A system whose temperature and pressure are kept constant and which does no work other than volume change work, assumes as its equilibrium state of all attainable states with this temperature and pressure the one in which the Gibbs energy has the smallest possible value.

To prove this, consider a closed system whose temperature and pressure are kept at a constant value. The temperature can be kept constant by keeping the system under consideration in contact, via a heat-permeable wall, with a second system that invariably has the desired temperature (in thermodynamic terms: a heat reservoir). In the event of a temperature difference, the system under consideration can exchange heat with the heat reservoir via a heat flow through the contact wall until it has brought its temperature back into line with that of the reservoir. The pressure can be kept constant by keeping the system in contact with a system that invariably has the desired pressure (a volume reservoir) via a heat-impermeable but flexible wall. By deforming the flexible wall, the system under consideration can "exchange volume" with the volume reservoir in the event of a pressure difference until it has brought its pressure back into line with that of the volume reservoir.

In the course of any process, the entropies of the system and the heat reservoir usually change (the volume reservoir exchanges no heat and no matter with the system under consideration, thus also no entropy). According to the Second Law of Thermodynamics, the entropy of the closed overall system formed by the system under consideration and the heat reservoir increases or at best remains the same:

$\mathrm {d} (S_{\mathrm {Sys} }+S_{\mathrm {Res} })=\mathrm {d} S_{\mathrm {Sys} }+\mathrm {d} S_{\mathrm {Res} }\geq 0$ ,

$\mathrm {d} S_{\mathrm {Sys} }\geq -\mathrm {d} S_{\mathrm {Res} }$ .

The "greater" sign applies to processes that increase the entropy of the overall system and therefore run voluntarily of their own accord. These processes run by themselves (provided there is no other inhibition) in the direction of the state of equilibrium. The equals sign applies when the overall system has assumed the greatest entropy achievable under the given conditions and has thus reached the thermal equilibrium state.

The entropy change $\mathrm {d} S_{\mathrm {Res} }$ of the reservoir is related to the heat flowing into the reservoir $\mathrm {d} Q_{\mathrm {Res} }$ and the temperature of the reservoir $T_{\mathrm {Res} }$ by definition in the relation

$\mathrm {d} S_{\mathrm {Res} }=\mathrm {d} Q_{\mathrm {Res} }/T_{\mathrm {Res} }$ .

Because the reservoir and the system under consideration exchange heat exclusively with each other, $\mathrm {d} Q_{\mathrm {Sys} }=-\mathrm {d} Q_{\mathrm {Res} }$ , and since the system and the reservoir are assumed to be at the same temperature, $T_{\mathrm {Sys} }=T_{\mathrm {Res} }$ . Therefore, it follows from the above inequality

$\mathrm {d} S_{\mathrm {Sys} }\geq \mathrm {d} Q_{\mathrm {Sys} }/T_{\mathrm {Sys} }$ .

This has made it possible to formulate the entropy criterion, which considers the entropies of system and reservoir, using only the quantities of the system under consideration, which greatly facilitates its application. Since a distinction is no longer necessary, the indices at the sizes of the system are now omitted and the inequality reads as follows

$\mathrm {d} S\geq \mathrm {d} Q/T$ (Clausius' inequality).

Furthermore, let it now be assumed that the system is kept under constant pressure (isobaric process, $\mathrm {d} p=0$ ) and that the system is also such that it cannot do any other kind of work except volume change work. Then the amount of heat added or removed is numerically equal to the enthalpy change of the system ( $\mathrm {d} H=\mathrm {d} Q$ , see → Enthalpy), and from Clausius' inequality follows

$\mathrm {d} S\geq \mathrm {d} H/T$

or converted

$\mathrm {d} H-T\,\mathrm {d} S\leq 0\quad (*)$ .

On the other hand, the change in the Gibbs energy of the system according to its definition is

$\mathrm {d} G=\mathrm {d} (H-T\,S)=\mathrm {d} U+p\mathrm {d} V+V\mathrm {d} p-T\mathrm {d} S-S\mathrm {d} T$ ,

which in the present case, because of the assumed constancy of temperature ( $\mathrm {d} T=0$ ) and pressure ( $\mathrm {d} p=0$ ) becomes

$\mathrm {d} G=\mathrm {d} H-T\,\mathrm {d} S\quad (*)$

simplified. Comparison of the marked equations (*) finally provides the statement:

$\mathrm {d} G\leq 0$ .

The "less than" sign applies to processes that run voluntarily. The equals sign applies as soon as the system has reached the state of equilibrium.

The maximum principle for the entropy of the total system thus leads to the Gibbs energy of the system under consideration assuming a minimum on the subset of states with constant temperature and constant pressure. If the system is not yet in equilibrium, it moves voluntarily (if isothermal and isobaric conditions exist and the system does no non-volume work) to states of lower Gibbs energy. Equilibrium is reached with the state in which the Gibbs energy has the smallest possible value under the given conditions.

If one wanted to directly determine the state of equilibrium with the help of the (generally and always valid) entropy criterion, the maximum of the total entropy would have to be determined, i.e. the sum of the entropies of the system under investigation and its environment. Therefore, not only the change of the system entropy during a change of state would have to be considered, but also the entropy change that the system produces there through feedback on the environment. The Gibbs energy criterion is a reformulation of the entropy criterion, into which only properties of the system under consideration enter and which automatically takes into account the retroaction on the environment (under isothermal and isobaric conditions) through the term $-T\,S$ , because under the given conditions $\mathrm {d} (-T\,S)=\mathrm {d} (T_{\mathrm {Res} }S_{\mathrm {Res} })$ . When using the Gibbs energy criterion, the determination of the (isothermal and isobaric) equilibrium state can thus be limited to the observation of the system, which noticeably facilitates the investigations.

For a real physical or chemical process, the atmosphere can often serve as a reservoir of heat and volume. Because of its large volume, its temperature and pressure do not change appreciably when a system transfers heat or volume to it. The conditions for the applicability of the minimum principle of Gibbs energy are thus fulfilled in particular when a system is exposed to the free atmosphere and its processes are therefore isothermal and isobaric. However, they are also fulfilled, for example, when a subsystem is considered within a larger system which, due to its size, represents a heat and volume reservoir for the subsystem (for example, for a grape in a fermentation vat).

Compare the minimum principle of the Gibbs energy under isothermal and isobaric conditions with the extreme principles of other thermodynamic potentials, which represent the equilibrium conditions in closed systems under other boundary conditions:

Constantly held sizes	Equilibrium condition
Internal energy and volume	Maximum entropy $S(U,V,n_{1},\dots ,n_{r})$
Entropy and Volume	Minimum internal energy $U(S,V,n_{1},\dots ,n_{r})$
Entropy and pressure	Minimum enthalpy $H(S,p,n_{1},\dots ,n_{r})$
Temperature and Volume	Minimum free energy $F(T,V,n_{1},\dots ,n_{r})$
Temperature and pressure	Minimum Gibbs energy $G(T,p,n_{1},\dots ,n_{r})$

In this section it has been assumed that the system does no work other than volume change work. The following section deals with systems that also do other forms of work.

Gibbs energy and maximum non-volume work

In the course of a process, a system usually exchanges heat and work with its environment. As will be shown in the following, in an isothermal, isobaric and reversible process, the decrease in the Gibbs energy of the system is numerically equal to the work done by the system on the environment, if any volume change work done $p\,\mathrm {d} V$ not taken into account.

Maximum non-volume work

If the enthalpy $H=U+p\,V$ a system changes in the course of a process, the following applies in general for a differential enthalpy change

The change of internal energy $\mathrm {d} U$ can be divided according to the First Law of Thermodynamics into the exchanged heat $\mathrm {d} Q$ and the exchanged work $\mathrm {d} W$ . The work in turn can be subdivided into volume change work $\mathrm {d} W_{V}$ and other forms of work (for example mechanical, electrical, chemical work), which are $\mathrm {d} W_{N}$ summarised as non-volume work

If the process is reversible,

according to the second law, the heat exchanged can be expressed by the entropy exchanged: $\mathrm {d} Q=T\mathrm {d} S$ ,
the volume change work done on the system is given by $\mathrm {d} W_{V}=-p\,\mathrm {d} V$ ,
maximum possible work is done on the system for the present change of state and it is $\mathrm {d} W_{N}=\mathrm {d} W_{N_{\mathrm {max} }}$ .

In this reversible case, the above equation can be written as

Finally, for the change in the Gibbs energy of the system associated with the process, according to its definition and using the expression just derived for $\mathrm{d}H$ :

${\begin{alignedat}{6}\mathrm {d} G&=\mathrm {d} (H-TS)&&&&&\\&=\mathrm {d} H&&&\,-\,&T\mathrm {d} S&\,-\,S\mathrm {d} T\\&=(T\mathrm {d} S&\,+\,&\mathrm {d} W_{N_{\mathrm {max} }}+V\mathrm {d} p)&\,-\,&T\mathrm {d} S&\,-\,S\mathrm {d} T\\&=&&\mathrm {d} W_{N_{\mathrm {max} }}+V\mathrm {d} p&&&\,-\,S\mathrm {d} T\end{alignedat}}$

If the process runs under isothermal ( $\mathrm {d} T=0$ ) and isobaric ( $\mathrm {d} p=0$ ) conditions, this simplifies to

$\mathrm {d} G=\mathrm {d} W_{N_{\mathrm {max} }}$ .

If one wants to count positively the work done by the system and made available to the environment, its sign must be reversed

$\mathrm {d} W'_{N_{\mathrm {max} }}=-\mathrm {d} W_{N_{\mathrm {max} }}$

and it is the work released

$\mathrm {d} W'_{N_{\mathrm {max} }}=-\mathrm {d} G$ .

Thus, if the Gibbs energy of a system changes in the course of an isothermal, isobaric and reversible process, the decrease in the Gibbs energy of the system is equal to the non-volumetric work delivered by the system to the environment during the process. Conversely, if non-volume work is done on the system, its Gibbs energy increases by the corresponding amount.

This relationship can be used, for example, to calculate the electrical work that can be obtained from electrochemical cells or from fuel cells. Conversely, from the measurement of the electrical work of a reaction, its Gibbs reaction energy Δ $\Delta_r G$ determined if an electrochemical cell can be operated with this reaction. By applying a suitably selected countervoltage, the cell can be operated close to the equilibrium state so that the electrochemical reaction is practically reversible and delivers the maximum possible electrical work.

Using a similar argument as above, it can be shown that the same relationship between non-volumetric work and Gibbs energy also applies to processes that temporarily assume different temperatures and pressures from the initial and final states. This is the case, for example, with combustion reactions. If one selects as the final state a state in which the system has again assumed the initial temperature - for example 20 °C - after combustion, then the entire process including heating and cooling is described by the Gibbs energies of the starting materials and products at 20 °C. However, free combustion is a reaction that takes place far from the state of equilibrium and thus irreversibly, so that it cannot deliver the maximum possible work output. If a process in which the system temporarily also assumes temperatures other than the temperature of the initial and final state and pressures other than the pressure of the initial and final state is to be conducted reversibly, it must be ensured in particular that, despite the variability of temperature and pressure, the heat exchange with the heat reservoir takes place at the temperature and the volume exchange with the pressure reservoir takes place at the pressure

If an isothermal, isobaric and non-reversible process takes place, then not all of the decrease in Gibbs energy is converted into non-volumetric work, a portion is given off as heat. In this case, the yield of non-volume work $\mathrm {d} W'_{N_{\mathrm {irrev} }}$ lower:

First example

As an example of the maximum non-volumetric work of a chemical reaction, determine the non-volumetric work that an organism can gain from the combustion of one mole of glucose at a body temperature of 37 °C and atmospheric pressure in order to maintain its functions (such as ultimately electrical nerve and muscle activity). The enthalpy of combustion for glucose is taken from relevant tables

$\Delta _{c}H=-2808\ \mathrm {\tfrac {kJ}{mol}}$

(the index c stands for combustion) and the entropy change associated with combustion.

$\Delta _{c}S=+182{,}4\ \mathrm {\tfrac {J}{K\ mol}}$ .

Strictly speaking, the figures apply to 25 °C and are used here approximately for 37 °C. Since enthalpy and entropy are state variables and therefore only depend on the initial and final state, these numerical values apply to the oxidation of glucose regardless of whether it takes place in an open combustion or - as here - in an enzymatically catalysed reaction. The Gibbs enthalpy of reaction is

$\Delta _{c}G=\Delta _{c}H-T\ \Delta _{c}S=-2808\ \mathrm {\tfrac {kJ}{mol}} -(310\ \mathrm {K} )\ (182{,}4\ \mathrm {\tfrac {J}{K\ mol}} )=-2865\ \mathrm {\tfrac {kJ}{mol}}$ .

Thus, from the combustion of one mole of glucose, a maximum of $2865\ \mathrm {kJ}$ non-volume work can be gained. If the combustion process proceeds non-reversibly, the recoverable work is less, depending on the extent of irreversibility.

Second example

In the derivation of the barometric height formula discussed below, a height-dependent term occurs in addition to a pressure-dependent term: The Gibbs energy of the volume element under consideration increases by the amount of the lifting work performed when the volume element is lifted in the gravitational field.

Processes without non-volume work

If an isothermal, isobaric and reversible process takes place, in the course of which the system does no non-volume work (i.e. no work at all, except possibly volume change work), then the free energy of the system does not change during this process:

$-\mathrm {d} G=\mathrm {d} W'_{N_{\mathrm {max} }}=0$ .

If, for example, part of a given quantity of water is converted by adding latent heat into a vapour phase that is in equilibrium with the rest of the water at the same temperature and pressure, then this isothermal, isobaric and reversible process involves volume change work (because of the expansion of the water during evaporation), but it does not perform any non-volume work. Consequently, the steam has the same molar Gibbs energy as the water with which it is in equilibrium. The equality of the molar Gibbs energy in different phases of a substance that are in equilibrium with each other will be discussed in more detail later.

If an isothermal, isobaric and irreversible process takes place, in the course of which the system does not perform any non-volumetric work

$\mathrm {d} W'_{N_{\mathrm {irrev} }}=0$ ,

then the inequality (see above) applies

$-\mathrm {d} G=\mathrm {d} W'_{N_{\mathrm {max} }}>\mathrm {d} W'_{N_{\mathrm {irrev} }}=0$ ,

Spontaneously occurring processes are always irreversible. Thus, if an isothermal and isobaric process, in the course of which the system does no non-volume work, runs spontaneously, it is associated with a decrease in the Gibbs energy. This result is already known from the previous section.

Derivatives of the Gibbs energy

Since the change in Gibbs energy is an important aspect in its application to thermodynamic processes, this section examines how it depends on its variables , and $n_{1},\dots ,n_{r}$ . In preparation, we first consider the derivatives of the internal energy and some related definitions.

The derivatives of the internal energy

Assuming the internal energy as a function of its natural variables $S,V,n_{1},\dots ,n_{r}$ and forming its total differential, we obtain:

$\mathrm {d} U(S,V,n_{1},\dots ,n_{r})=\left({\frac {\partial U}{\partial S}}\right)_{V,n_{1},\dots ,n_{r}}\mathrm {d} S+\left({\frac {\partial U}{\partial V}}\right)_{S,n_{1},\dots ,n_{r}}\mathrm {d} V\,+\,\sum _{i=1}^{r}\left({\frac {\partial U}{\partial n_{i}}}\right)_{S,V,n_{j\neq i}}\mathrm {d} n_{i}$ .

The partial derivatives occurring here are interpreted in thermodynamics as the definitions of temperature , pressure and chemical potential of the ith substance μ $\mu _{i}$ :

$T:=\left({\frac {\partial U(S,V,n_{1},\dots ,n_{r})}{\partial S}}\right)_{V,n_{1},\dots ,n_{r}}$

$p:=-\left({\frac {\partial U(S,V,n_{1},\dots ,n_{r})}{\partial V}}\right)_{S,n_{1},\dots ,n_{r}}$

$\mu _{i}:=\left({\frac {\partial U(S,V,n_{1},\dots ,n_{r})}{\partial n_{i}}}\right)_{S,V,n_{j\neq i}}$ .

With these definitions, the differential of the internal energy can also be written as

$\mathrm {d} U(S,V,n_{1},\dots ,n_{r})=T\,\mathrm {d} S-p\,\mathrm {d} V\,+\,\sum _{i=1}^{r}\mu _{i}\,\mathrm {d} n_{i}$ .

The derivatives of Gibbs energy

The total differential of the Gibbs energy as a function of its natural variables $T,p,n_{1},\dots ,n_{r}$ is on the one hand formally

$\mathrm {d} G(T,p,n_{1},\dots ,n_{r})=\left({\frac {\partial G}{\partial T}}\right)_{p,n_{1},\dots ,n_{r}}\mathrm {d} T+\left({\frac {\partial G}{\partial p}}\right)_{T,n_{1},\dots ,n_{r}}\mathrm {d} p\,+\,\sum _{i=1}^{r}\left({\frac {\partial G}{\partial n_{i}}}\right)_{T,p,n_{j\neq i}}\mathrm {d} n_{i}\quad (*)$ .

and on the other hand, using their definition and using the expression just derived for $\mathrm {d} U$ :

${\begin{alignedat}{13}\mathrm {d} G&\,=\mathrm {d} (U&&&&&\,+\,&pV&&&\,-\,&TS)&&\\&\,=\mathrm {d} U&&&&&\,+\,&p\,\mathrm {d} V&\,+\,&V\,\mathrm {d} p&\,-\,&T\,\mathrm {d} S&\,-\,&S\mathrm {d} T\\&\,=T\,\mathrm {d} S&\,-\,&p\,\mathrm {d} V&\,+\,&\sum \mu _{i}\,\mathrm {d} n_{i}&\,+\,&p\,\mathrm {d} V&\,+\,&V\,\mathrm {d} p&\,-\,&T\,\mathrm {d} S&\,-\,&S\mathrm {d} T\\&\,=&&&&\sum \mu _{i}\,\mathrm {d} n_{i}&&&\,+\,&V\,\mathrm {d} p&&&\,-\,&S\mathrm {d} T\\\end{alignedat}}$

so converted

$\mathrm {d} G=-S\,\mathrm {d} T+V\,\mathrm {d} p\,+\,\sum \mu _{i}\,\mathrm {d} n_{i}\quad (*)$

so that from the comparison of the coefficients in the marked equations (*) follows

$\left({\frac {\partial G}{\partial T}}\right)_{p,n_{1},\dots ,n_{r}}=-S$ ,

and

$\left({\frac {\partial G}{\partial p}}\right)_{T,n_{1},\dots ,n_{r},\dots }=V$

and

$\left({\frac {\partial G}{\partial n_{i}}}\right)_{T,p,n_{j\neq i}}=\mu _{i}$ .

These simple relationships are discussed in more detail in the following sections.

The derivation shows at the same time how the addition of the terms $-T\,S$ and $p\,V$ the list of independent variables from $(S,V,\dots )$ to $(T,p,\dots )$ removing the terms dependent on $\mathrm {d} V$ $\mathrm{d}S$ and the total differential and adding terms dependent on ${\mathrm {d}}p$ $\mathrm {d} T$ and instead.

The second of the marked equations is a "differential fundamental function", namely the frequently required differential Gibbs energy as a function of its natural variables:

$\mathrm {d} G(T,p,n_{1},\dots ,n_{r})=-S\,\mathrm {d} T+V\mathrm {d} p\,+\,\sum _{i=1}^{r}\mu _{i}\,\mathrm {d} n_{i}$ .

Gibbs energy and chemical potential

→ Main article: Chemical potential

Consider a homogeneous phase with temperature and pressure consisting of a mixture of substances, where in each case the i}th substance is present in the quantity $n_{i}$ From the equation derived above

$\left({\frac {\partial G}{\partial n_{i}}}\right)_{T,p,n_{j\neq i}}=\mu _{i}$

follows a descriptive interpretation of the chemical potential μ $\mu _{i}$ :

The chemical potential μ $\mu _{i}$ the -th component of the phase indicates by which (infinitesimal) amount $\mathrm {d} G$ Gibbs energy of the phase changes, if the amount of the component in the phase changes by the (infinitesimal) amount $\mathrm {d} n_{i}$ , where the temperature , the pressure and the quantities $n_{j}$ the remaining components are kept constant. The amount of the th component may change, for example, in the course of a chemical reaction taking place in the phase, or because it is added to the phase from the environment (which may also be another phase of the system).

The transition from the infinitesimal quantity $\mathrm {d} G$ to the total Gibbs energy the system seems to require an integration at first. This would also be difficult because $\mathrm {d} G$ may depend in a complicated way on the quantities of substances present $n_{1},\dots ,n_{r}$ , which in turn may change in a complicated way during the process. However, it turns out that the relationship between $\mathrm {d} G$ (respectively the μ $\mu _{i}$ ) and surprisingly simple.

The starting point of the considerations is the generally valid differential fundamental function derived above

$\mathrm {d} G=-S\,\mathrm {d} T+V\,\mathrm {d} p+\mu _{1}\,\mathrm {d} n_{1}+\dots +\mu _{r}\,\mathrm {d} n_{r}$ .

Now think of the size of the phase multiplied. In this process, the temperature and the pressure remain unchanged because they are intensive quantities. So in this case $\mathrm {d} T=0$ and $\mathrm {d} p=0$ and the differential simplifies to

$\mathrm {d} G=\mu _{1}\,\mathrm {d} n_{1}+\dots +\mu _{r}\,\mathrm {d} n_{r}$ .

Since the chemical potentials μ $\mu _{1},\dots ,\mu _{r}$ are also intensive quantities, they also remain unchanged. The direct integration of the differential therefore yields

${\begin{aligned}\Delta G=\int \mathrm {d} G&=\int \mu _{1}\,\mathrm {d} n_{1}+\dots +\int \mu _{r}\,\mathrm {d} n_{r}\\&=\mu _{1}\int \mathrm {d} n_{1}+\dots +\mu _{r}\int \mathrm {d} n_{r}\\&=\mu _{1}\Delta n_{1}+\dots +\mu _{r}\Delta n_{r},\end{aligned}}$

because the μ $\mu _{1},\dots ,\mu _{r}$ can be drawn in front of the respective integrals as constant quantities.

If the phase is increased to then the numerical values of the extensive quantities , $n_{1}$ ... $n_{r}$ to times and the following applies

$\Delta G=k\,G-G=(k-1)\,G$

$\Delta n_{i}=k\,n_{i}-n_{i}=(k-1)\,n_{i}$

Substituting into the previous equation leads to

$(k-1)G=\mu _{1}(k-1)n_{1}+\dots +\mu _{r}(k-1)n_{r}$

and thus

$G=n_{1}\mu _{1}+\dots +n_{r}\mu _{r}$ .

There is therefore a simple relationship between the Gibbs energy of the phase and the chemical potentials of the substances contained in the phase:

If each chemical potential μ $\mu _{i}$ is multiplied by the quantity $n_{i}$ the substance concerned and the sum is formed over all substances, the result is equal to the Gibbs energy of the phase.

Both and the μ $\mu _{i}$ are only determined to one constant.

Division by the total amount of substance the phase gives the often used Gibbs molar energy

${\frac {G}{n}}={\frac {n_{1}}{n}}\mu _{1}+\dots +{\frac {n_{r}}{n}}\mu _{r}=x_{1}\mu _{1}+\dots +x_{r}\mu _{r}$

with the mass fractions $x_{i}=n_{i}/n$ .

For a system consisting of only one substance ( r=1 ) is in particular

${\frac {G}{n}}=\mu$ .

In a multi-component system, the chemical potentials are thus identical to the partial molar Gibbs energies of the system. In a single-component system, the chemical potential is identical to the molar Gibbs energy of the system.

Chemical potential in phases in equilibrium

Thermodynamic potentials usually assume different values in the different phases of a system. For example, the molar enthalpies of water and water vapour, which are in equilibrium, differ by the amount of the enthalpy of vaporisation of water. The chemical potential, on the other hand, assumes the same value in all phases of a system in equilibrium.

To prove this, consider a single-component system consisting of several phases in equilibrium and first assume that the chemical potential has different values μ $\mu _{A}$ and μ different locations and the system $\mu _{B}$ . If one imagines a quantity of substance transported $\mathrm{d}n$ from location to location Gibbs energy at location changes by the amount $-\mu _{A}\mathrm {d} n$ and at location by the amount $+\mu _{B}\mathrm {d} n$ , so the total Gibbs energy of the system changes by $\mathrm {d} G=(\mu _{B}-\mu _{A})\mathrm {d} n$ . If μ $\mu _{B}<\mu _{A}$ then the change in Gibbs energy is negative and transport proceeds spontaneously, contradicting the assumption that the system is already in equilibrium. Thus, the system can only be in equilibrium if μ $\mu _{A}=\mu _{B}$ .

Since the two locations compared can be in different phases but also in the same phase, the equality of the chemical potential follows in all phases but also at all locations within each phase.

Since in the considered case of a single substance the chemical potential is identical with the molar Gibbs energy, the constancy of the molar Gibbs energy also follows in all phases.

Temperature dependence of the Gibbs energy

→ Main article: Gibbs-Helmholtz equation

Temperature dependence

From the equation derived above

$\left({\frac {\partial G}{\partial T}}\right)_{p,n_{1},\dots ,n_{r}}=-S$

it follows directly that the temperature dependence of the Gibbs energy at constant pressure and constant quantities of substances is given by the negative of the entropy of the system. Since entropy is always positive according to the third law of thermodynamics, the Gibbs energy always decreases under these conditions when the temperature increases. In gases with their high entropy, the temperature dependence of the Gibbs energy is greater than in liquids or solids.

Division by the amount of substance in the phase yields the corresponding equation for the molar quantities of the phase:

$\left({\frac {\partial G_{m}}{\partial T}}\right)_{p,x_{1},\dots ,x_{r-1}}=-S_{m}$

Example

As an example of temperature dependence, consider ice and liquid water, which are in equilibrium. Let the temperature common to the two phases be the melting temperature corresponding to the common pressure (for example, 0 °C if the pressure is atmospheric pressure). Since equilibrium is assumed, both phases have the same Gibbs molar energy:

$G_{m,\ \mathrm {Eis} }(T)=G_{m,\ \mathrm {Wasser} }(T)$ .

If the temperature is increased while the pressure is kept constant, the molar Gibbs energies change proportionally to the negative of their respective molar entropies:

${\begin{alignedat}{7}&G_{m,\ \mathrm {Eis} }(T')&&\,=\,G_{m,\ \mathrm {Eis} }(T)&&-S_{m,\ \mathrm {Eis} }&&\mathrm {d} T\\&G_{m,\ \mathrm {Wasser} }(T')&&\,=\,G_{m,\ \mathrm {Wasser} }(T)&&-S_{m,\ \mathrm {Wasser} }&&\mathrm {d} T.\end{alignedat}}$

Since the liquid water has the greater molar entropy compared to the ice with its lattice structure, its molar Gibbs energy decreases faster with an increase in temperature, and it eventually has a smaller molar Gibbs energy than the ice at the increased final temperature. The equilibrium between the two phases is therefore disturbed. It could be restored either by the ice melting and assuming the smaller Gibbs molar energy of water, or by the water freezing and assuming the larger Gibbs molar energy of ice. As the melting process (at constant pressure and new temperature kept constant) decreases the Gibbs energy of the total system, it is the melting process that the system selects and spontaneously goes through until a new equilibrium is established.

Conversely, if the temperature is reduced, the Gibbs molar energy of the water increases more than that of the ice and the disturbed equilibrium is spontaneously restored as the water freezes and matches the smaller Gibbs molar energy of the ice.

Pressure dependence of the Gibbs energy

Pressure dependence

From the equation derived above

$\left({\frac {\partial G}{\partial p}}\right)_{T,n_{1},\dots ,n_{r}}=V$

it follows directly that the pressure dependence of the Gibbs energy at constant temperature and constant quantities of substances is given by the volume of the system. Since the volume is always positive, the Gibbs energy always increases under these conditions when the pressure increases.

Division by the amount of substance in the phase yields the corresponding equation for the molar quantities of the phase:

$\left({\frac {\partial G_{m}}{\partial p}}\right)_{T,x_{1},\dots ,x_{r-1}}=V_{m}$ .

Example

As an example of pressure dependence, consider again ice and liquid water, which are in equilibrium. Since equilibrium is assumed, both phases have the same Gibbs molar energy:

$G_{m,\ \mathrm {Eis} }(p)=G_{m,\ \mathrm {Wasser} }(p)$

If the pressure is increased while the temperature is kept constant, the molar Gibbs energies change proportionally to the respective molar volume:

${\begin{alignedat}{7}&G_{m,\ \mathrm {Eis} }(p')&&\,=\,G_{m,\ \mathrm {Eis} }(p)&&+V_{m,\ \mathrm {Eis} }&&\mathrm {d} p\\&G_{m,\ \mathrm {Wasser} }(p')&&\,=\,G_{m,\ \mathrm {Wasser} }(p)&&+V_{m,\ \mathrm {Wasser} }&&\mathrm {d} p.\end{alignedat}}$

Since the ice has the larger molar volume compared to the liquid water, its molar Gibbs energy increases faster with an increase in pressure, and it eventually has a higher molar Gibbs energy than the water at the increased final pressure. The equilibrium between the two phases is disturbed. It is restored by the ice melting and assuming the smaller Gibbs molar energy of water. Since this melting process (at constant temperature and new pressure) decreases the total Gibbs energy of the system, the melting occurs spontaneously.

Despite the temperature being kept constant, the system under increased pressure is now completely liquid. The temperature would therefore have to be reduced to allow equilibrium between liquid water and ice again at the new pressure: The increase in pressure has lowered the melting temperature. The properties of the state variable Gibbs energy allowed this conclusion to be drawn solely from knowledge of the molar volumes of ice and liquid water.

Conversely, if the pressure is reduced, the Gibbs molar energy of the ice decreases faster than that of the water and the disturbed equilibrium is spontaneously restored as the water freezes and converges to the smaller Gibbs molar energy of the ice.

Conclusions

If the Gibbs energy is $p^{\circ }$ known at a reference pressure, for example the standard pressure , it can be determined for any other pressures by integration:

$G(p)=G(p^{\circ })+\int _{p^{\circ }}^{p}V\,\mathrm {d} p$ .

The following applies accordingly to the Gibbs molar energy:

$G_{m}(p)=G_{m}(p^{\circ })+\int _{p^{\circ }}^{p}V_{m}\,\mathrm {d} p$ .

For liquids and solids, the molar volume $V_{m}$ varies only slightly with the pressure. $V_{m}$ can then be approximately regarded as constant and drawn in front of the integral:

$G_{m}(p)=G_{m}(p^{\circ })+(p-p^{\circ })\,V_{m}$ .

For not too extreme pressure increases, $(p-p^{\circ })\,V_{m}$ usually negligible and the Gibbs energy of liquids and solids is practically independent of pressure:

$G_{m}(p)=G_{m}(p^{\circ })$

With gases, on the other hand, the molar volume varies too much to be set constant. Here the integral must be evaluated.

Gibbs energy of the ideal gas

In the case of ideal gases, the integral can be calculated immediately, since the molar volume can be expressed as

$V_{m}={\frac {R\,T}{p}}$

can be expressed and inserted into the integral:

${\begin{aligned}G_{m}(p)&=G_{m}(p^{\circ })+R\,T\,\int _{p^{\circ }}^{p}{\frac {1}{p}}\mathrm {d} p\\&=G_{m}(p^{\circ })+R\,T\,\ln \left({\frac {p}{p^{\circ }}}\right).\end{aligned}}$

For a system consisting of only one substance, the Gibbs energy m $G_{m}$ identical to the chemical potential μ $\mu$ the substance (see above) and the following applies

$\mu =\mu ^{\circ }+R\,T\,\ln \left({\frac {p}{p^{\circ }}}\right)$ ,

where the Gibbs molar energy of the substance in the standard state, $G_{m}(p^{\circ })$ , is now called the chemical potential of the substance in the standard state, μ $\mu ^{\circ }$ , is denoted.

The chemical potential of an ideal gas can therefore be easily calculated as a function of pressure. This has many applications, because it is not only possible to determine the chemical potential of approximately ideal gases in this way. If, for example, one considers a liquid that is in equilibrium with its vapour, then the molar Gibbs energy - and thus also the chemical potential - is identical in both phases (see above), and the chemical potential of the liquid is therefore known, provided the vapour may be treated as an ideal gas to a sufficiently good approximation.

Gibbs energy of a solvent

As an example, consider a solution, i.e. a mixture of a solvent and a substance dissolved in it. According to Raoult's law, the vapour pressure solvent is proportional to the amount of substance with which it is represented in the solution:

$p\,=\,c\,x$ .

(In most cases, Raoult's law is only valid in the limiting case of strongly diluted solutions; in the following, its validity for the solution under consideration is assumed). If the solute fraction of the solvent is changed from $x_{0}$ to , the corresponding vapour pressures $p_{0}$ and behave like the solute fractions:

${\frac {p}{p_{0}}}\,=\,{\frac {x}{x_{0}}}$ .

If one further assumes that the solvent vapour may be treated as an ideal gas to a sufficient approximation, then the formula from the last section is applicable and for the chemical potentials μ $\mu _{0}$ and μ $\mu$ the vapour above the two solvent fractions considered:

$\mu =\mu _{0}+R\,T\,\ln \left({\frac {p}{p_{0}}}\right)=\mu _{0}+R\,T\,\ln \left({\frac {x}{x_{0}}}\right)$ .

If one chooses the pure solvent as the starting point (indicated by an asterisk ∗ $^{*}$ ), then because $x_{0}=x^{*}=1$ the chemical potential of the solvent vapour over the solvent with fraction

$\mu =\mu ^{*}+R\,T\,\ln(x)$ .

Because the solvent is in equilibrium with its vapour, it has the same chemical potential. Since the solute fraction of the solvent is less than one, its logarithm has a negative sign. The presence of a dissolved substance thus reduces the chemical potential of the solvent under the conditions mentioned. This is the cause of phenomena such as osmosis, lowering of the freezing point in solutions and the like.

If the mass fraction of the dissolved substance is denoted by $x_{2}:=1-x$ , then

${\begin{aligned}\mu &=\mu ^{*}+R\,T\,\ln(x)\\&=\mu ^{*}+R\,T\,\ln(1-x_{2})\\&\approx \mu ^{*}-R\,T\,x_{2},\end{aligned}}$

the chemical potential of the solvent thus decreases proportionally to the molar fraction of the dissolved substance. Note that the change in the chemical potential of the solvent does not depend on the nature of the dissolved substance, but only on its mass fraction, see → colligative property.

Gibbs mixing energy of ideal gases

Consider a container with two chambers containing the pure gases respectively. Let their quantities be $n_{\mathrm {A} }$ and $n_{\mathrm {B} }$ (with $n_{\mathrm {A} }+n_{\mathrm {B} }=n$ ). Let their temperatures be equal, as well as their pressures . Since the Gibbs energy is an extensive quantity, the Gibbs energy of the total system is calculated as the sum of the Gibbs energies of both subsystems. If one uses the molar Gibbs energies, which in turn are identical with the chemical potentials, one obtains

$G_{\mathrm {Anfang} }=n_{\mathrm {A} }\ G_{\mathrm {m,A} }+n_{\mathrm {B} }\ G_{\mathrm {m,B} }=n_{\mathrm {A} }\ \mu _{\mathrm {A} }+n_{\mathrm {B} }\ \mu _{\mathrm {B} }$ .

In particular, if the gases are ideal, then the Gibbs energy using the formula derived in the previous section for the chemical potential of an ideal gas:

$G_{\mathrm {Anfang} }=n_{\mathrm {A} }\left(\mu _{\mathrm {A} }^{\circ }+R\,T\,\ln \left({\frac {p}{p^{\circ }}}\right)\right)+n_{\mathrm {B} }\left(\mu _{\mathrm {B} }^{\circ }+R\,T\,\ln \left({\frac {p}{p^{\circ }}}\right)\right)$ .

If the partition between the chambers is removed, the gases mix. In the mixed state they have the partial pressures $p_{\mathrm {A} }$ and $p_{\mathrm {B} }$ (with $p_{\mathrm {A} }+p_{\mathrm {B} }=p$ ). With these pressures, the Gibbs energy of the system in the mixed final state is

$G_{\mathrm {Ende} }=n_{\mathrm {A} }\left(\mu _{\mathrm {A} }^{\circ }+R\,T\,\ln \left({\frac {p_{\mathrm {A} }}{p^{\circ }}}\right)\right)+n_{\mathrm {B} }\left(\mu _{\mathrm {B} }^{\circ }+R\,T\,\ln \left({\frac {p_{\mathrm {B} }}{p^{\circ }}}\right)\right)$ .

The difference between the Gibbs energies in the final and initial states is the Gibbs mixing energy Δ $\Delta _{\mathrm {mix} }G$ :

$\Delta _{\mathrm {mix} }G=G_{\mathrm {Ende} }-G_{\mathrm {Anfang} }=n_{\mathrm {A} }\ R\,T\,\ln \left({\frac {p_{\mathrm {A} }}{p}}\right)+n_{\mathrm {B} }\ R\,T\,\ln \left({\frac {p_{\mathrm {B} }}{p}}\right)$ .

According to Dalton's law, the partial pressure $p_{\mathrm {A} }$ expressed as the product of the mass fraction $x_{\mathrm {A} }$ and total pressure :

$p_{\mathrm {A} }=x_{\mathrm {A} }\ p$ .

Furthermore, due to the definition of the substance amount fraction

$n_{\mathrm {A} }=x_{\mathrm {A} }\ n$ ,

and corresponding expressions also apply in each case to gas . This gives the Gibbs mixing energy of ideal gases:

$\Delta _{\mathrm {mix} }G=n\ R\,T\,(x_{\mathrm {A} }\ln x_{\mathrm {A} }+x_{\mathrm {B} }\ln x_{\mathrm {B} })$ .

Since the mass fractions according to their definition are always smaller than one in the case under consideration, the logarithms always become negative and the Gibbs mixing energy is also always negative. The Gibbs energy of the total system of ideal gases therefore always decreases during mixing and the mixing of ideal gases is therefore a voluntary process, which also corresponds to experience with real but approximately ideal gases.

If strongly non-ideal substances are mixed, other formulas for the Gibbs mixing energy result. It can then even assume positive values under certain circumstances. In such a case, a mixture segregates voluntarily, the components involved are not miscible. If the Gibbs mixing energy only assumes positive values in a certain range of compositions of the mixture, the mixture is only unstable for these compositions - there is a mixing gap.

In the considered case of non-reacting ideal gases, the substance quantities of both components remained constant during the mixing process. If the mixed substances can react chemically with each other, the amounts of substances are variable. They then voluntarily adjust themselves so that the Gibbs mixing energy assumes the smallest value compatible with the conditions of the reaction. The state that is established in this way is the state of chemical equilibrium. The position of this state of equilibrium can therefore be predicted if the Gibbs mixing energy of the system is known.

Application

Osmosis

→ Main article: Osmosis

The effect of osmosis can be seen, for example, when a solvent containing dissolved substances is separated from pure solvent by a membrane that is permeable to the solvent but impermeable to the dissolved substances. Pure solvent then flows spontaneously through the membrane into the solution, even without a pressure difference being present.

For further explanation, consider a phase that is a mixture of a solvent and solutes. It is in contact with a second phase consisting of the pure solvent via a semi-permeable membrane that is only permeable to the solvent. An example would be a phase with sugar water and a phase with pure water, which are separated from each other by a cellophane foil. Temperature and pressure would be identical on both sides.

In the mixture, the solvent has a lower chemical potential than in the pure state (compare the above discussion of the Gibbs energy of a solvent). The different chemical potentials of the solvent in the two phases set in motion a balancing solvent flow that transports solvent from the side with the higher chemical potential to the side with the lower chemical potential (namely the side with the mixture).

If one wants to prevent osmotic transport, one must cause the solvent to have the same chemical potential both in the pure phase and in the mixed phase. This can be done by departing from the requirement of equal pressure on both sides and increasing the pressure in the mixed phase (while keeping the temperatures identical). As explained above, an increase in pressure increases the chemical potential. The additional pressure $\Pi$ which must be applied to achieve equilibrium is called osmotic pressure. If the pressure in the pure solvent and $p^{\prime }$ is the pressure in the mixture, then in equilibrium

$\Pi =p'-p$ .

Let the chemical potential of the pure solvent be denoted by μ $\mu _{p}^{*}$ ; the asterisk denotes the pure substance and the index the pressure under which the substance is.

For the mixing phase, let it be assumed for the sake of simplicity that it is an ideal mixture. Then the chemical potential of the solvent (mass fraction ) in the mixed phase under pressure is given by

$\mu _{p'}^{*}+R\,T\,\ln x$ .

In osmotic equilibrium, the two chemical potentials are equal:

$\mu _{p}^{*}=\mu _{p'}^{*}+R\,T\,\ln x$ ,

or converted and taking into account the pressure dependence of the chemical potential of the pure solvent:

${\begin{aligned}R\,T\,\ln x&=\mu _{p}^{*}-\mu _{p'}^{*}\\&=\int _{p'}^{p}V_{m}\ \mathrm {d} p,\end{aligned}}$

where $V_{\mathrm {m} }$ is the molar volume of the pure solvent. With ${\overline {V}}_{\mathrm {m} }$ as the mean value of the molar volume over the pressure interval $p-p'$ it becomes:

$R\,T\,\ln x={\overline {V}}_{\mathrm {m} }\,(p-p')=-{\overline {V}}_{\mathrm {m} }\ \Pi$ .

The following therefore applies to the osmotic pressure:

$\Pi =-{\frac {R\,T}{{\overline {V}}_{\mathrm {m} }}}\,\ln x$ .

With $\textstyle \sum x_{\mathrm {i} }$ as the sum over the mass fractions of all dissolved substances is

$\Pi =-{\frac {R\,T}{{\overline {V}}_{\mathrm {m} }}}\,\ln(1-\sum x_{\mathrm {i} })$ ,

which for small $\textstyle \sum x_{\mathrm {i} }$ becomes

$\Pi \approx {\frac {R\,T}{{\overline {V}}_{\mathrm {m} }}}\,\sum x_{\mathrm {i} }$

simplified, van 't Hoff's law. The osmotic pressure of sufficiently diluted solutions is therefore proportional to the sum of the mass fractions of the dissolved substances.

Clausius-Clapeyron equation

→ Main article: Clapeyron equation

→ Main article: Clausius-Clapeyron equation

In the above discussion of the temperature and pressure dependence of the Gibbs energy, it was shown that an existing equilibrium of two phases of a substance is disturbed if either the temperature of the system is changed while the pressure is kept constant or the pressure of the system is changed while the temperature is kept constant. However, it is possible to change pressure and temperature together so that the phases remain in equilibrium, provided that the changes $\mathrm {d} T$ and ${\mathrm {d}}p$ suitably matched.

If the considered system of two phases and a substance is initially in equilibrium, the specific Gibbs energies of the two phases are equal. After the changes $\mathrm {d} T$ and ${\mathrm {d}}p$ the phases should also be in equilibrium, their specific Gibbs energies must therefore - usually with changed numerical values - again be equal. The specific Gibbs energies of both phases must therefore have changed by the same amount:

$\mathrm {d} g_{1}=\mathrm {d} g_{2}$ .

Since the system consists of only one substance, the differential Gibbs function (see above) reduces to the expression $\mathrm {d} g=-s\,\mathrm {d} T+v\,\mathrm {d} p$ , and from

$v_{1}\,\mathrm {d} p-s_{1}\,\mathrm {d} T=v_{2}\,\mathrm {d} p-s_{2}\,\mathrm {d} T$

follows the Clapeyron equation

${\frac {\mathrm {d} p}{\mathrm {d} T}}={\frac {s_{2}-s_{1}}{v_{2}-v_{1}}}$ .

The difference $s_{2}-s_{1}$ is the difference of the specific entropies of both phases. It is identical to the specific latent enthalpy Δ $\Delta h$ which must be supplied to a unit mass of the substance at the given temperature and pressure in order to transfer it reversibly from phase to phase , divided by the temperature present :

$s_{2}-s_{1}={\frac {\Delta h}{T}}$ .

Substituting this expression yields the Clausius-Clapeyron equation:

${\frac {\mathrm {d} p}{\mathrm {d} T}}\,=\,{\frac {\Delta h}{T\,\Delta v}}$ .

Vapour pressure over drops

→ Main article: Kelvingleichung

The saturation vapour pressure of a liquid at a given temperature is the pressure at which the liquid is in equilibrium with its vapour. It is usually assumed that the surface of the liquid is flat. Over curved surfaces, the saturation vapour pressure assumes other values: It is higher over convexly curved surfaces (e.g. over drops) and lower over concavely curved surfaces (e.g. over the meniscus in a partially filled capillary) than over a flat surface.

The reason for this is the changed pressure under which the liquid is subjected with a curved surface. With a flat surface (since equilibrium is assumed), the pressure in the liquid phase is equal to the pressure in the vapour phase. However, the liquid in a drop of radius is under a higher pressure because the surface tension γ $\gamma$ an additional capillary pressure

$p_{\mathrm {k} }=2\gamma /r$

is generated in the drop. The total pressure in the drop is the sum of the capillary pressure and the saturation vapour pressure exerted by the vapour phase on the drop. What is sought is the new saturation vapour pressure that must occur over the curved surface under these changed pressure conditions in order to maintain equilibrium.

The pressure dependence of the saturation vapour pressure can be $\mu _{\mathrm {g} }$ determined by considering the pressure dependence of the chemical potentials of the liquid μ $\mu _{\mathrm {l} }$ and the vapour μ (the index l stands for liquid, the index g for gas). In any equilibrium of liquid and vapour, the chemical potentials of the two phases are equal:

$\mu _{\mathrm {g} }=\mu _{\mathrm {l} }$ .

If a change occurs that leads to a new equilibrium, in general μ $\mu _{\mathrm {g} }$ and μ change, but they remain the same among themselves, so both must change in the same way: μ $\mu _{\mathrm {l} }$ but they remain the same among themselves, so they must both change in the same way:

$\mathrm {d} \mu _{\mathrm {g} }=\mathrm {d} \mu _{\mathrm {l} }$ .

If the change is a pressure change $\mathrm {d} p_{\mathrm {l} }$ in the fluid, then the chemical potential of the fluid (see pressure dependence of Gibbs energy) changes by

$\mathrm {d} \mu _{\mathrm {l} }=V_{\mathrm {m,l} }\,\mathrm {d} p_{\mathrm {l} }$ ,

where $V_{\mathrm {m,l} }$ is the molar volume of the liquid. A corresponding expression applies to the vapour phase and it follows

$V_{\mathrm {m,g} }\,\mathrm {d} p_{\mathrm {g} }=V_{\mathrm {m,l} }\,\mathrm {d} p_{\mathrm {l} }$ .

From this equation it can be determined what pressure change $\mathrm {d} p_{\mathrm {g} }$ in the vapour phase is necessary to re-establish equilibrium if the pressure in the liquid phase changes by $\mathrm {d} p_{\mathrm {l} }$

For simplicity, assume that the vapour behaves like an ideal gas. Its molar volume is then given by $V_{\mathrm {m,g} }=R\,T/p_{\mathrm {g} }$ and the following applies

${\frac {\mathrm {d} p_{\mathrm {g} }}{p_{\mathrm {g} }}}={\frac {V_{\mathrm {m,l} }\,\mathrm {d} p_{\mathrm {l} }}{R\,T}}$

This formula is now integrated, from the initial state without additional pressure to the final state in which there is an additional pressure Δ $\Delta p$ liquid. In the initial state, the pressures in the vapour and in the liquid are equal to the normal saturation vapour pressure $p_{0}$ . In the final state, the pressure in the liquid is Δ p $\Delta p$ increased by $p_{0}+\Delta p$ in the vapour the pressure to be determined prevails:

$\int _{p_{0}}^{p}{\frac {\mathrm {d} p_{\mathrm {g} }}{p_{\mathrm {g} }}}={\frac {1}{R\,T}}\int _{p_{0}}^{p_{0}+\Delta p}V_{\mathrm {m,l} }\,\mathrm {d} p_{\mathrm {l} }$ .

If, as a further simplification, it is assumed that the molar volume of the liquid is constant in the pressure range under consideration (i.e. the liquid is incompressible), the following follows

${\begin{aligned}\ln \left({\frac {p}{p_{0}}}\right)&={\frac {V_{\mathrm {m,l} }}{R\,T}}\,(p_{0}+\Delta p-p_{0})\\&={\frac {V_{\mathrm {m,l} }}{R\,T}}\,\Delta p\end{aligned}}$

or transformed

$p=p_{0}\,e^{\frac {V_{\mathrm {m,l} }\,\Delta p}{R\,T}}$ .

This formula describes how the saturation vapour pressure increases from $p_{0}$ to when an additional pressure Δ $\Delta p$ is applied to the liquid, regardless of the way in which the pressure increase Δ } $\Delta p$ was generated in the liquid.

An open water surface, for example, is exposed to atmospheric pressure instead of only its own saturation vapour pressure; the saturation vapour pressure in humid atmospheric air is therefore slightly higher than in a pure water vapour atmosphere at the same temperature (Poynting effect). Thus, the saturation vapour pressure of pure water at equilibrium with an atmosphere consisting only of water vapour is 612 Pa at the triple point. If air is added to the vapour phase until the total atmospheric pressure of 101325 Pa is reached, the equilibrium partial pressure of the water vapour in the mixture of vapour and air (in the so-called "humid air") is 0.5 Pa higher than in the pure water vapour atmosphere because of the pressure increase of a good ^{105 Pa.}

If the pressure increase is due to capillary forces because a drop of radius now considered instead of the liquid with a plane surface, then Δ $\Delta p=2\gamma /r$ and the following applies to the saturation vapour pressure above the drop

$p_{\mathrm {Tr} }=p_{0}\,e^{\frac {2\gamma \,V_{\mathrm {m,l} }}{R\,T\,r}}$

This is the Kelvin equation. Above a water droplet with a radius of 0.001 mm, for example, the saturation vapour pressure at 25 °C is greater by a factor of 1.001 than above a flat water surface. Over a concave meniscus with the same radius, the saturation vapour pressure is lower by the same factor.

Barometric altitude formula

→ Main article: Barometric altitude formula

This short alternative derivation of the barometric height formula demonstrates the change in Gibbs energy of a volume element in a fluid when the acting hydrostatic pressure changes and when non-volume work is done on the element.

Let there be a vertical column of a fluid (for example water or air) in equilibrium in the homogeneous gravitational field of field strength ${\overline {g}}$ . The Gibbs energy of a volume element is investigated as a function of its height in the fluid column. For this purpose, it is assumed that the volume element has been transported from a point to a point at a different height. The change of its specific (i.e. related to the mass) Gibbs energy during this process consists of two contributions:

The change in hydrostatic pressure along the path changes the specific Gibbs energy by

$\Delta g_{P}=\int _{A}^{B}v\,\mathrm {d} P$ ,

where is the specific volume of the fluid under the respective pressure.

The specific work done on the volume element (assumed to be reversible) during the height change Δ $\Delta h$ is non-volume work, it therefore increases the specific Gibbs energy of the volume element by

$\Delta g_{W}=\mathrm {d} w_{N_{\mathrm {max} }}=\int _{A}^{B}{\overline {g}}\,\mathrm {d} h$ .

Overall, the specific Gibbs energy changes with the height change by

$\Delta g=\Delta g_{P}+\Delta g_{W}=\int _{A}^{B}v\,\mathrm {d} P+\int _{A}^{B}{\overline {g}}\,\mathrm {d} h$ .

Since the fluid column is assumed to be in equilibrium, the specific Gibbs energy must have the same value at all heights, so it is Δ $\Delta g=0$ from which follows

$v\,\mathrm {d} P+{\overline {g}}\,\mathrm {d} h=0$ .

Converting and inserting the density ρ $\textstyle \rho ={\frac {1}{v}}$ yields

${\frac {\mathrm {d} P}{\mathrm {d} h}}=-{\frac {\overline {g}}{v}}=-{\overline {g}}\,\rho$ .

This is the well-known relationship between the change in altitude and the change in hydrostatic pressure in a fluid. Integrating this equation gives the barometric altitude formula.

Chemical reaction equilibrium of ideal gases

→ Main article: Mass action law

Introductory example

As an introductory example, consider a simple chemical equilibrium reaction of the type

$\mathrm {A\rightleftharpoons B}$

which takes place at constant temperature and constant pressure. The system initially consists of pure starting material and the product increasingly formed from it. Since it is presumed to be an equilibrium reaction, a reconversion from to also takes place at the same time (it could be an isomerisation, for example, which can proceed in both directions). The reconversion rate is initially zero, since no exists yet. However,the more has been formed $A\to B$ by the outward reaction , the greater the reverse conversion rate also becomes. At a certain composition of the chemical system, the outward and backward reactions occur at the same conversion rate and the composition of the system no longer changes - the equilibrium composition is reached. Since experience shows that such a system voluntarily enters this state and the process presupposedly takes place under isothermal and isobaric conditions, the equilibrium composition is characterised by the fact that it is the composition with the smallest Gibbs energy. This fact allows the expected equilibrium composition to be calculated.

The progress of the reaction is $\xi$ measured by the turnover variable ξ In the initial state, ξ $\xi$ has the value zero. When one mole has been converted in the reaction, so the amount of substance of decreased by one mole and the amount of substance of has increased by one mole, then ξ has $\xi$ reached the value 1 mole, and so on.

The reaction proceeds according to the premise at constant temperature and constant pressure, in the differential fundamental function $\mathrm {d} G$ (see above)

$\mathrm {d} G=-S\ \mathrm {d} T+V\ \mathrm {d} p+\mu _{A}\ \mathrm {d} n_{A}+\mu _{B}\ \mathrm {d} n_{B}$

the ${\mathrm {d}}p$ terms dependent on $\mathrm {d} T$ and dropped and for the change $\mathrm {d} G$ of only the terms

${\begin{aligned}(\mathrm {d} G)_{T,p}&=\mu _{A}\ \mathrm {d} n_{A}+\mu _{B}\ \mathrm {d} n_{B}\\&=-\mu _{A}\ \mathrm {d} \xi +\mu _{B}\ \mathrm {d} \xi \end{aligned}}$

Rearrangement yields the equation

$\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=\mu _{B}-\mu _{A}$ .

This equation gives for a given mixture of and in which reaction direction the Gibbs energy decreases, i.e. in which direction the system runs voluntarily starting from the present mixture. Decisive for this are the chemical potentials μ $\mu _{A}$ and μ $\mu _{B}$ . In the case μ right side $\mu _{B}<\mu _{A}$ negative, G {\displaystyledecreases in the positive reaction direction, so the reaction proceeds in of B {\displaystyle case μ B > $\mu _{B}>\mu _{A}$ direction of A {\displaystyle As the reaction proceeds, the chemical potentials dependent on the mixture also change, and as soon as $\mu _{A}=\mu _{B}$ , $\mathrm {d} G=0$ . The Gibbs energy has reached the minimum and the system has reached its equilibrium where its composition no longer changes. The general thermodynamic equilibrium condition for such a chemical system is therefore simple

$0=\mu _{B}-\mu _{A}$

$\mu _{B}=\mu _{A}$ .

This also shows the reason for the name "chemical potential": The chemical system strives for a "potential balance" and has reached equilibrium when the two chemical potentials have become equal.

If the reacting substances are ideal gases in particular, the expressions derived above can be used for their chemical potentials as a function of the partial pressures p_A and p_B

${\begin{aligned}\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}&=\mu _{B}-\mu _{A}\\&=\mu _{B}^{\circ }+RT\ \ln \left({\frac {p_{B}}{p^{\circ }}}\right)-\mu _{A}^{\circ }-RT\ \ln \left({\frac {p_{A}}{p^{\circ }}}\right)\\&=\mu _{B}^{\circ }-\mu _{A}^{\circ }+RT\ \ln \left({\frac {p_{B}}{p_{A}}}\right)\end{aligned}}$ .

The derivative $\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}$ on the left describes the change in Gibbs energy per mole of formula conversion at the present composition of the reacting mixture. It is also briefly called Gibbs reaction energy Δ $\Delta_r G$

The chemical potential μ $\mu _{A}^{\circ }$ standard state and therefore to the pure substance . For this case, however, as described above, the chemical potential is identical to the Gibbs molar energy. The difference μ $\mu _{B}^{\circ }-\mu _{A}^{\circ }$ is therefore equal to the difference $G_{m,B}^{\circ }-G_{m,A}^{\circ }$ of the molar Gibbs energies of the pure substances and the standard state. This difference is also $\Delta _{r}G^{\circ }$ called the standard Gibbs molar reaction energy Δ

The equation can be written shorter with these definitions as

$\Delta _{r}G=\Delta _{r}G^{\circ }+RT\ \ln \left({\frac {p_{B}}{p_{A}}}\right)$ .

At equilibrium, Δ $\Delta _{r}G=0$ , thus

$-{\frac {\Delta _{r}G^{\circ }}{RT}}=\ln \left({\frac {p_{B}}{p_{A}}}\right)$

${\frac {p_{B}}{p_{A}}}=e^{-{\frac {\Delta _{r}G^{\circ }}{RT}}}=:K$

While the individual values p_A and p_B co-determined by the existing initial quantities and can assume different values for differently set experiments in equilibrium, their ratio in the state of equilibrium is determined solely by Δ $\Delta _{r}G^{\circ }$ and the temperature. Thus, for given substances and and given temperature, there is a constant, the equilibrium constant . Equilibrium is reached as soon as the ratio of the partial pressures has assumed this numerical value.

General case

In the general case of a reaction with a more complex stoichiometry, which is

$a\ A+b\ B+\dots \,=\,p\ P+q\ Q+\dots$

is symbolised, the reaction equation is rearranged as in the transformation of a mathematical equation so that all the summands are on the right-hand side and a reaction equation of the form

$0=\sum _{J}\nu _{J}\ J$ .

Here the stoichiometric number νassociated with substance has a $\nu _{J}$ negative sign for the starting substances on the left-hand side of the original equation and a positive sign for the products on the right-hand side.

If the turnover variable ξ $\xi$ by ${\mathrm {d}}\xi$ , then the amount of substance according to its stoichiometric number by $\mathrm {d} n_{J}=\nu _{J}\ \mathrm {d} \xi$ and the change in the Gibbs energy in the course of the isothermal and isobaric reaction is

$(\mathrm {d} G)_{T,p}=-S\ \mathrm {d} T+V\ \mathrm {d} p+\sum _{J}\mu _{J}\ \mathrm {d} n_{J}=\sum _{J}\mu _{J}\ \nu _{J}\ \mathrm {d} \xi$ .

Convert results in

$\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=\sum _{J}\nu _{J}\ \mu _{J}$ .

In the state of equilibrium the left side is zero and the general thermodynamic equilibrium condition for a reaction with this stoichiometry is

$0=\sum _{J}\nu _{J}\ \mu _{J}$ .

Here, the system thus strives to balance the chemical potentials weighted with the (partly positive, partly negative) stoichiometric numbers.

If the reacting substances are ideal gases in particular, the known expressions for their chemical potentials can be used again. Using the definition for the Gibbs reaction energy $\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=:\Delta _{r}G$ and the definition of standard Gibbs molar reaction energy extended to multiple summands $\sum _{J}\nu _{J}\ \mu _{J}^{\circ }=:\Delta _{r}G^{\circ }$ :

${\begin{aligned}\Delta _{r}G&=\sum _{J}\nu _{J}\ \mu _{J}\\&=\sum _{J}\nu _{J}\left(\mu _{J}^{\circ }+RT\ \ln \left({\frac {p_{J}}{p^{\circ }}}\right)\right)\\&=\left(\sum _{J}\nu _{J}\ \mu _{J}^{\circ }\right)+RT\ \sum _{J}\nu _{J}\ \ln \left({\frac {p_{J}}{p^{\circ }}}\right)\\&=\Delta _{r}G^{\circ }+RT\ \sum _{J}\ln \left({\frac {p_{J}}{p^{\circ }}}\right)^{\nu _{J}}\\&=\Delta _{r}G^{\circ }+RT\ \ln \prod _{J}\left({\frac {p_{J}}{p^{\circ }}}\right)^{\nu _{J}}\end{aligned}}$

In the state of equilibrium, Δ $\Delta _{r}G=0$ , thus

$-{\frac {\Delta _{r}G^{\circ }}{RT}}=\ln \prod _{J}\left({\frac {p_{J}}{p^{\circ }}}\right)^{\nu _{J}}$

$\prod _{J}\left({\frac {p_{J}}{p^{\circ }}}\right)^{\nu _{J}}=e^{-{\frac {\Delta _{r}G^{\circ }}{RT}}}=:K$

For example, if the reaction is

$2\ A+3\ B\rightleftharpoons C+2\ D$

then the corresponding stoichiometric numbers are ν $\nu _{A}=-2$ , ν $\nu _{B}=-3$ , ν $\nu _{C}=1$ and ν $\nu _{D}=2$ .

The general thermodynamic equilibrium condition for any substance , , and is

$0=-2\ \mu _{A}-3\ \mu _{B}+\mu _{C}+2\ \mu _{D}$ .

In particular, if it is an ideal gas mixture, then using the formulae for the chemical potentials of ideal gases gives the standard Gibbs molar reaction energy

$\Delta _{r}G_{m}^{\circ }=-2\mu _{A}^{\circ }-3\ \mu _{B}^{\circ }+\mu _{C}^{\circ }+2\ \mu _{D}^{\circ }$

and the equilibrium constant

$K=e^{-{\frac {\Delta _{r}G^{\circ }}{RT}}}$ .

For the partial pressures the equilibrium condition follows

${\frac {\left({\frac {p_{C}}{p^{\circ }}}\right)\left({\frac {p_{D}}{p^{\circ }}}\right)^{2}}{\left({\frac {p_{A}}{p^{\circ }}}\right)^{2}\left({\frac {p_{B}}{p^{\circ }}}\right)^{3}}}=K$ .

Here, too, the resulting numerical values for $p_{A},\dots ,p_{D}$ among other things, on the initial quantities used, but the expression mentioned for the ratio of the partial pressures is determined solely by Δ $\Delta _{r}G_{m}^{\circ }$ as well as the temperature, is thus for the substances $A,\dots ,D$ and the given temperature in a reaction of the given stoichiometry is a constant, the equilibrium constant . The reaction has reached the state of equilibrium as soon as the ratio of the partial pressures satisfies the above equilibrium condition.

To determine the standard Gibbs molar reaction energy Δ $\Delta _{r}G_{m}^{\circ }$ only the Gibbs molar energies of the pure substances involved in the standard state are required, which can be taken from relevant tables.

Electrochemistry

In electrochemistry (see electrochemical voltage series), the useful work performed by a voluntary conversion of chemical substances (e.g. a fuel cell) can be determined via the following relationship:

$\Delta _{\mathrm {r} }G=-z\cdot F\cdot E$

with

$\Delta _{\mathrm {r} }G$ - molar free enthalpy of reaction
- number of electrons transferred in the reaction under consideration.
- Faraday constant: 96485.3399(24) A s/mol
- equilibrium cell tension

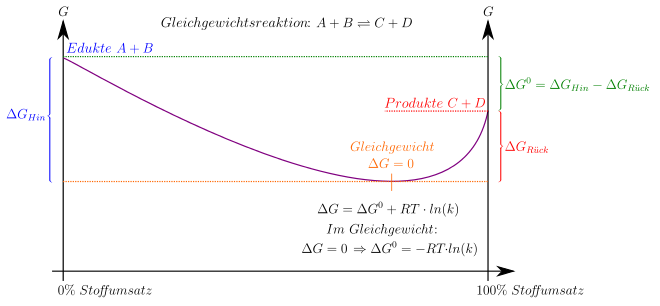
Change in Gibbs energy during an equilibrium reaction. The complete conversion of the reactants is not achieved because there is always a back reaction of the products.

Gibbs energy as a fundamental function

Consider a system whose properties are determined by the state variables entropy , volume and molar numbers $n_{1},\dots ,n_{r}$ the chemical components, then the internal energy the system is expressed as a function of the mentioned state variables (namely all extensive variables of the system),

$U=U(S,V,n_{1},\dots ,n_{r})$

a fundamental function of the system. It describes the system completely; all thermodynamic properties of the system can be derived from it.

Often, however, these variables are inconvenient for practical work and one would prefer to have, for example, the temperature or the pressure in the variable list. In contrast to the usual procedure, a change of variables in the present case must not be done by a simple substitution, as otherwise information is lost. For example, if the entropy is to be replaced by the temperature could be derived from the functions $U(S,V,n_{i})$ and $T(S,V,n_{i})$ to obtain a function of the form $U(T,V,n_{i})$ However, since the temperature is thermodynamically defined as the partial derivative of the internal energy according to the entropy

$T=\left({\frac {\partial U}{\partial S}}\right)_{V,n_{1},\dots ,n_{r}}$

this formulation would be equivalent to a partial differential equation for which would define only up to indefinite functions. This would still be a description of the system under consideration, but it would not be a complete description and thus no longer a fundamental function.

To change variables while preserving the complete information, a Legendre transformation must be performed. For example, if the variable list $(T,p,n_{1},\dots ,n_{r})$ , the transformation is as follows:

${\begin{aligned}G(T,p,n_{1},\dots ,n_{r})&:=U(S,V,n_{1},\dots ,n_{r})-\left({\frac {\partial U}{\partial S}}\right)_{V,n_{1},\dots ,n_{r}}\cdot S-\left({\frac {\partial U}{\partial V}}\right)_{S,n_{1},\dots ,n_{r}}\cdot V\\&=U-T\,S+p\,V\\&=H-T\,S\end{aligned}}$

The Legendre transform $G=H-T\ S$ is called Gibbs energy. It is again a fundamental function if it is given as a function of the variables $(T,p,n_{1},\dots ,n_{r})$ - these are the natural variables of the Gibbs energy. It can also be expressed as a function of other variables, but then it is no longer a fundamental function.

The origin of the Gibbs energy from a Legendre transformation explains the additive terms $-T\,S$ and $p\,V$ : They compensate for the loss of information that would otherwise be associated with the change of variable.

The following table shows some examples of how other thermodynamic quantities can be derived from the fundamental function "Gibbs energy":

Equations of state:

$s(T,p)=-\left({\frac {\partial g}{\partial T}}\right)_{p}$

$v(T,p)=\left({\frac {\partial g}{\partial p}}\right)_{T}$

$h(T,p)=g-T\left({\frac {\partial g}{\partial T}}\right)_{p}$

Derivatives of the caloric equations of state:

$c_{p}(T,p):=\left({\frac {\partial h}{\partial T}}\right)_{p}=-T\left({\frac {\partial ^{2}g}{\partial T^{2}}}\right)_{p}$

$\left({\frac {\partial h}{\partial p}}\right)_{T}=v-T\left({\frac {\partial v}{\partial T}}\right)_{p}$

Derivatives of entropy:

$\left({\frac {\partial s}{\partial T}}\right)_{p}={\frac {c_{p}(T,p)}{T}}$

$\left({\frac {\partial s}{\partial p}}\right)_{T}=-\left({\frac {\partial v}{\partial T}}\right)_{p}$

Gibbs free energy

Overview

Gibbs energy as equilibrium criterion

Chemical potential

Change in the Gibbs energy of a system

As a fundamental equation

Minimum principle of Gibbs energy

Gibbs energy and maximum non-volume work

Maximum non-volume work

First example

Second example

Processes without non-volume work

Derivatives of the Gibbs energy

The derivatives of the internal energy

The derivatives of Gibbs energy

Gibbs energy and chemical potential

Chemical potential in phases in equilibrium

Temperature dependence of the Gibbs energy

Temperature dependence

Example

Pressure dependence of the Gibbs energy

Pressure dependence

Example

Conclusions

Gibbs energy of the ideal gas

Gibbs energy of a solvent

Gibbs mixing energy of ideal gases

Application

Osmosis

Clausius-Clapeyron equation

Vapour pressure over drops

Barometric altitude formula

Chemical reaction equilibrium of ideal gases

Introductory example

General case

Electrochemistry

Gibbs energy as a fundamental function

Search by letter