Gamma function

The Eulerian gamma function, also known as the gamma function or Eulerian integral of the second genus, is one of the most important special functions and is studied in the mathematical subfields of calculus and function theory. It is represented today by a Γ $\Gamma$ , the Greek capital gamma, and is a transcendental meromorphic function with property

$\Gamma (n)=(n-1)!$

for any natural number , where with denotes the factorial. The motivation for defining the gamma function was to be able to extend the factorial to real and complex arguments. In 1729, the Swiss mathematician Leonhard Euler solved this problem and defined the gamma function using an infinite product. Today, the gamma function is often defined by means of an integral representation, which also goes back to Euler.

The gamma function underlies the gamma probability distribution.

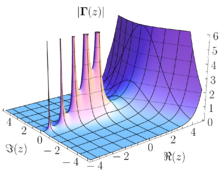
magnitude of the complex gamma function

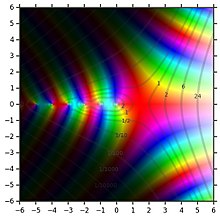
Complex gamma function: The brightness corresponds to the magnitude, the color to the argument of the function value. Additionally, contour lines of constant magnitude are drawn.

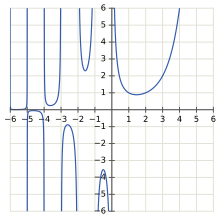
Graph of the gamma function in the real

Classification without prior mathematical knowledge

A mathematical function is basically like a calculator. You enter a value into the function, and it then returns a result depending on the input value, at least in theory. What is meant by this is that the function itself does not calculate, but mostly just holds a calculation rule in a formulaic way. A simple example of a function is the quadratic function, which multiplies the input by itself. Formulaically, this is written as $f(x)=x^{2}$ . Thus, for example, the quadratic function assigns the value $(-2)^{2}$ to the number Calculating this, we get $4$ , so $f(-2)=4$ .

The gamma function is based on a rule also known as the factorial. This assigns to a natural number the product of all natural numbers up to this number. The factorial is denoted by the symbol of the exclamation mark. So for example

$4!=1\cdot 2\cdot 3\cdot 4=24.$

It was considered a problem within mathematics whether this rule could be extended to numbers of other kinds. Concretely, this means:

Can factorials also be calculated for arbitrary rational, real, complex numbers? How about you could think of $({\tfrac {1}{2}})!$ ?
If such "universal" rules are found, what mathematical properties can be given to them? Does one of these prescriptions stand out as being particularly natural and structural? Is this particular precept uniquely determined, i.e. "the one" generalized factorial?

The answer to these questions is provided by the gamma function. For any value , Γ $\Gamma (z+1)=z!$ , so, for example, Γ $\Gamma (5)=24.$ The shift of 1 from the above factorial is due to a 19th century convention. The strategy of generalization is based on the observation that another factorial is obtained from a previous factorial by adding another factor. Thus, for example, $4!\cdot 5=5!$ and more generally $n!\cdot (n+1)=(n+1)!$ . Accordingly, all values of the gamma function should be related by Γ . $\Gamma (z)\cdot z=\Gamma (z+1)$ If one imposes other important conditions, such as differentiability, on Γ $\Gamma (z)$ then this can finally be uniquely defined, with which "the" generalized factorial is found.

It then holds $({\tfrac {1}{2}})!=\Gamma ({\tfrac {3}{2}})={\tfrac {\sqrt {\pi }}{2}}\approx 0{,}88622$ with circle number π $\pi$ . This relationship can be explained by Gaussian normal distribution.

History

The earliest definition of the gamma function is considered to be that given in a letter from Daniel Bernoulli to Christian Goldbach on 6 October 1729:

$\Bigl(A + \frac{x}{2}\Bigr)^{x-1} \Bigl(\frac{2}{1+x} \cdot \frac{3}{2+x} \cdot \frac{4}{3+x} \cdots \frac{A}{A-1+x}\Bigr)$

for infinitely large , according to today's notation or Γ $\Gamma(x+1)$ . A few days later, on 13 Octoberjul^. / 24 October 1729greg^. , Euler also described in a letter to Goldbach the similar, somewhat simpler formula

${\frac {1\cdot 2\cdot 3\dotsm n}{(1+m)(2+m)\dotsm (n+m)}}\,(n+1)^{m},$

which Gauss rediscovered in 1812 for the more general case of complex numbers (the letters mentioned were not published until 1843). It approaches with increasing the true value for or Γ $\Gamma(m+1)$ . On January 8, 1730, in a letter to Goldbach, Euler described the following integral for the interpolation of the factorial function, which he had presented to the St. Petersburg Academy on November 28, 1729:

$\int \!{\mathrm d}x(-lx)^{n},$ in present notation: Γ $\displaystyle \Gamma (n+1)=\int _{0}^{1}(-\log x)^{n}\mathrm {d} x$

This definition was later preferred by Euler and goes by the substitution $t = -\log x$ into the form

$\Gamma (n+1)=\int _{0}^{\infty }t^{n}{\mathrm {e}}^{{-t}}{\mathrm d}t$

about. Euler discovered this integral while studying a problem from mechanics in which the acceleration of a particle is considered.

In 1809, Adrien-Marie Legendre introduced the Greek majuscule Γ $\Gamma$ (gamma) as a function symbol. In 1812, Gauss used the function symbol $\Pi$ (Pi) such that $\Pi(x) = \Gamma(x+1)$ and thus also holds $\Pi(n) = n!$ for nonnegative integer However, it did not catch on; today $\Pi$ used as a symbol for a product (analogous to $\Sigma$ for a sum).

Questions and Answers

Q: What is the gamma function in mathematics?

A: The gamma function is a key topic in the field of special functions in mathematics.

Q: What is the extension of the factorial function to all complex numbers except negative integers?

A: The gamma function is an extension of the factorial function to all complex numbers except negative integers.

Q: How is the gamma function defined for positive integers?

A: For positive integers, the gamma function is defined as Γ(n) = (n-1)!.

Q: Is the gamma function defined for all complex numbers?

A: Yes, the gamma function is defined for all complex numbers.

Q: Is the gamma function defined for negative integers and zero?

A: No, the gamma function is not defined for negative integers and zero.

Q: How is the gamma function defined for a complex number whose real part is not a negative integer?

A: The gamma function is defined for a complex number whose real part is not a negative integer by a specific formula that is not given in the text.

Q: Why is the gamma function important in mathematics?

A: The gamma function is important in mathematics because it is a key topic in the field of special functions and it extends the factorial function to all complex numbers except negative integers.