Finite set

In set theory, a branch of mathematics, a finite set is a set with finitely many elements. For example, the set

$M\,=\,\{4,6,2,8\}$

is a finite set with four elements. According to its definition, the empty set has no elements, i.e. the number of elements is $0$ , so it is also considered to be a finite set. The power or cardinality, written |M| for a set , of a finite set is identified with a natural number (involving zero). For example, one then writes |M|=4 to express that consists of four elements.

A set that is not finite is called an infinite set.

Definition

A set is called finite if there exists a natural number such that a bijection (a one-to-one mapping)

$f\colon M\rightarrow N_{n}\quad :=\{m\in \mathbb {N} _{0}\,\mid \,m<n\}\;=\;\{0,1,2,3,\dotsc ,n-1\}$

exists between and the set $N_{n}$ of all natural numbers less than

In particular, the empty set $\emptyset :=\{\}$ finite, since a bijection between $\emptyset$ and the empty set $N_{0}$ (all natural numbers less than $0$ , such do not exist) trivially exist.

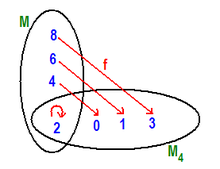
For example, the amount

$M\,=\,\{4,6,2,8\}$

finite, since a bijection to the set

$N_{4}\,=\,\{0,1,2,3\}$

exists, see for example the figure opposite.

With this enumerative set notation, the order is not important. Furthermore, an element that is mentioned more than once is only included once. It is therefore for example

$M\,=\,\{4,6,2,8\}\,=\,\{2,4,6,8\}\,=\,\{4,8,6,2,6,8\}\,=\,\{4,8,6,2,6,4,6,4,6,4,6,4,\dotsc \}$ .

For the set of all natural numbers

$\mathbb {N} _{0}=\{0,1,2,3,\dotsc \}$

on the other hand, no such bijection exists on a finite set, the set $\mathbb {N} _{0}$ is therefore infinite.

The bijection indicated by the red arrows shows $|M|=|N_{4}|$ and thus the finiteness of

Basic properties of finite sets

Any subset of a finite set is also finite.
In particular, if a finite set and is an arbitrary set, then both the intersection $A\cap B$ and the difference $A\setminus B$ finite sets, because both are subsets of .
If are finite sets, then their union $A\cup B$ is also finite. For their powers, $|A\cup B|=|A|+|B|-|A\cap B|$ .
If and
are finite and disjoint, that is, $A\cap B=\emptyset ,$ then one has $|A\cup B|=|A|+|B|=|A\,{\dot {\cup }}\,B|$ .
In general, a union of finitely many finite sets is again a finite set. Its power is given by the principle of inclusion and exclusion.
If is infinite and is finite, then is $A\setminus B$ infinite.
The power set ${\mathcal {P}}(A):=\{U\mid U\subseteq A\}$ of a finite set has power greater than the set itself, but is still finite; it holds $|{\mathcal {P}}(A)|=2^{|A|}$ .
The Cartesian product $A \times B$ of finite sets is finite. Its power is higher than that of all factors involved if no factor is empty and at least two factors have power greater than . For finite sets , $|A\times B|=|A|\cdot |B|$ . More generally, a Cartesian product of finitely many finite sets is again a finite set.