Exponential distribution

The exponential distribution (also negative exponential distribution) is a continuous probability distribution over the set of non-negative real numbers given by an exponential function. It is primarily used as a model in answering the question of the length of random time intervals, such as

Time between two calls
Lifetime of atoms during radioactive decay
Service life of components, machines and devices, when ageing phenomena do not have to be considered.
as a rough model for small and medium losses in household contents, motor vehicle liability, comprehensive insurance in actuarial mathematics

$\lambda$ represents the number of expected events per unit interval. As can be seen from the diagram, shorter intervals between events (interval length ) are more likely. However, very long intervals occur less frequently. The probability density may well take values >1 (e.g. for λ $\lambda = 2$ ), since the area under the curve is normalized to 1 (normalization property). Concrete probability information about the occurrence of the next event is best obtained here from the distribution function.

Often the actual distribution is not an exponential distribution, but the exponential distribution is easy to handle and is assumed for simplicity. It is applicable if a Poisson process is present, i.e. the Poisson assumptions are fulfilled.

The exponential distribution is part of the much larger and more general exponential family, a class of probability measures characterized by ease of use.

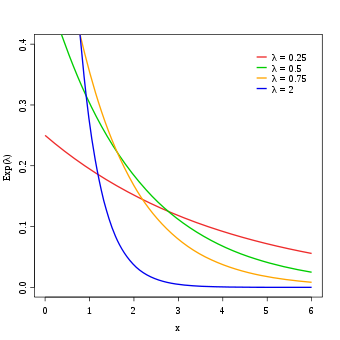
Density of the exponential distribution with different values for λ

Definition

A continuous random variable satisfies the exponential distribution $\operatorname {Exp}(\lambda )$ with the positive real inverse scale parameter λ $\lambda \in \mathbb{R} _{{>0}}$ , if they have the density function

$f_{{\lambda }}(x)={\begin{cases}\displaystyle \lambda {{\rm {e}}}^{{-\lambda x}}&x\geq 0\\0&x<0\end{cases}}$

has. If a random variable has this density, then one also writes $X\sim {\mathcal {E}}(\lambda )$ or $X\sim \operatorname {Exp} (\lambda )$ .

The parameter λ $\lambda$ has the character of an event rate and $1/\lambda$ that of an event distance (mean range or mean lifetime).

An alternative parameterization (common especially in Anglo-Saxon countries) leads to the density function

$f_{{\mu }}(x)={\begin{cases}\displaystyle {\frac {1}{\mu }}{\mathrm {e}}^{{-{\frac {x}{\mu }}}}&x\geq 0\\0&x<0\end{cases}}$ .

The relation to the above parametrization is simply μ $\mu =1/\lambda$ . To avoid misunderstandings, it is recommended to state the expected value explicitly, i.e. to speak of an exponential distribution with expected value . $1/\lambda$

Relationship to other distributions

Relationship to the continuous uniform distribution

If a continuous random variable uniformly [0,1] distributed on the interval , then $Y=-{\tfrac {1}{\lambda }}\ln(X)$ satisfies the exponential distribution with parameter λ $\lambda$ .

Relationship to normal distribution

If the random variables and are standard normally distributed and independent, then $X^{2}+Y^{2}$ is exponentially distributed with parameter λ $\lambda ={\tfrac 12}$ .

Relationship to geometric distribution

In analogy to the discrete geometric distribution, the continuous exponential distribution determines the waiting time until the first occurrence of an event that occurs according to a Poisson process; thus, the geometric distribution can be considered as a discrete equivalent of the exponential distribution.

Relationship to gamma distribution

The generalization of the exponential distribution, i.e. the waiting time until the arrival of the -th event of a Poisson process, is described by the gamma distribution. Thus, the exponential distribution with parameter λ $\lambda$ is identical to the gamma distribution with parameters and λ $\lambda$ . Accordingly, the exponential distribution also has all the properties of the gamma distribution. In particular, the sum of independent, $\operatorname {Exp}(\lambda )$ -distributed random variables is gamma or Erlang distributed with parameters and λ $\lambda$ .

Convolving two exponential distributions with the same λ $\lambda$ yields a gamma distribution with , $b=\lambda$ .

Relationship to gamma-gamma distribution

If the parameter λ $\lambda$ of the exponential distribution $\operatorname {Exp}(\lambda )$ a random variable distributed like a gamma distribution G(a,b) , then the resulting random variable is G(a,b,1) distributed like a gamma-gamma distribution .

Relationship to the Pareto distribution

If is Pareto distributed $\operatorname {Par}(\lambda ,1)$ with parameters λ $\lambda$ and then is $\log {X}$ exponentially distributed $\operatorname {Exp}(\lambda )$ with parameter λ $\lambda$ .

Relationship to the Poisson distribution

The distances between the occurrence of random events can often be described by the exponential distribution. In particular, it holds that the distance between two consecutive events of a Poisson process with rate λ is $\lambda$ exponentially distributed with parameter λ . $\lambda$ In this case, the number of events in an interval of length Δ is $\Delta w$ Poisson distributed with parameter λ $\lambda \cdot \Delta w$ .

Derivation: Let w be a location or time variable and λ $\lambda$ the small constant occurrence frequency of events in the unit interval of w . Then, using Poisson's assumptions, find the probability of the next occurrence of an event in the small interval $[w,w+\Delta w]$ as the product of the probability of having no event up to w and one in the interval : $[w,w+\Delta w]$

$P_{1}(w+\Delta w)={\mathrm {e}}^{{-\lambda \cdot w}}\cdot \lambda \Delta w$

From this, after dividing by Δ $\Delta w$ the probability density $f_{{\lambda }}(w)=\lambda {\mathrm {e}}^{{-\lambda \cdot w}}$ of the exponential distribution with λ $\lambda$ as event rate and $1/\lambda$ as mean event distance.

Relationship to the Erlang distribution

For a Poisson process, the random number of events up to a defined time is determined by means of Poisson distribution, the random time up to the -th event is Erlang distributed. In the case , this Erlang distribution transitions to an exponential distribution $\operatorname {Erl}(\lambda ,1)=\operatorname {Exp}(\lambda )$ , which can be used to determine the time to the first random event and the time between two consecutive events.

The sum of independent $\operatorname {Exp}(\lambda )$ exponentially distributed random variables has the Erlang distribution -th order $\operatorname {Erl}(\lambda ,n)$ .

Relationship to Weibull distribution

With β $\beta =1$ , the Weibull distribution transitions to the exponential distribution. In other words, the exponential distribution handles problems with constant failure rate λ $\lambda$ . However, if one examines problems with increasing ( $\lambda >1$ ) or decreasing ( $\lambda <1$ ) failure rate, then one transitions from the exponential distribution to the Weibull distribution.
If is exponentially distributed, then $X^{\lambda }$ Weibull distributed.

Relationship to the chi-square distribution

The chi-squared distribution transitions to the exponential distribution for n=2 with parameter λ $\lambda ={\tfrac {1}{2}}$

Relationship to the Rayleigh distribution

If is exponentially distributed with rate λ $\lambda$ , then is ${\sqrt {X}}$ Rayleigh distributed with scale parameter ${\frac {1}{\sqrt {2\lambda }}}$ .

Relationship to the Laplace distribution

If are $X_{\lambda },Y_{\lambda }$ two independent random variables, both exponentially distributed to parameter λ , $\lambda$ then both $X_{\lambda }-Y_{\lambda }$ and $Y_{\lambda }-X_{\lambda }$ Laplace distributed.

Relationship to the standard Gumbel minimum distribution

The density of the logarithm of a standard exponentially distributed random variable $X\sim \operatorname {Exp} (\lambda =1)$ follows a standard Gumbel distribution (minimum)

$f(z)=\operatorname {exp} \left(z\right)\operatorname {exp} \left(-\operatorname {exp} \left(z\right)\right)$ .