Euler–Mascheroni constant

This is the sighted version that was marked on 18 May 2021. There is 1 pending change that needs to be sighted.

Euler's constant is a redirection to this article. For other numbers named after Euler, see Euler's numbers (disambiguation).

The Euler-Mascheroni constant (after the mathematicians Leonhard Euler and Lorenzo Mascheroni), also Euler's constant, is an important mathematical constant that occurs particularly in the fields of number theory and analysis. It is denoted by the Greek letter γ $\gamma$ (gamma).

Their definition is:

$\gamma =\lim _{n\to \infty }\left(H_{n}-\ln n\right)=\lim _{n\rightarrow \infty }\left(\sum _{k=1}^{n}{\frac {1}{k}}-\ln n\right)=\int _{1}^{\infty }\left({1 \over \lfloor x\rfloor }-{1 \over x}\right)\,\mathrm {d} x,$

where $H_{n}$ denotes the nth harmonic number, $\ln$ the natural logarithm and ⌊ $\lfloor x\rfloor$ the rounding function.

Its numerical value is accurate to 100 decimal places (sequence A001620 in OEIS):

γ = 0,57721 56649 01532 86060 65120 90082 40243 10421 59335 93992 35988 05767 23488 48677 26777 66467 09369 47063 29174 67495 …

As of May 2020, calculation completed on 26 May 2020, 600,000,000,100 decimal decimal places are known.

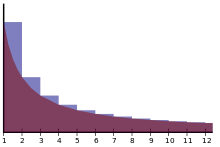
The blue area represents Euler's constant.

General

Despite great efforts, it is still unknown whether this number is rational or irrational, whether it is algebraic or transcendental. However, it is strongly suspected that it is at least an irrational number. The first concrete attempt to prove this was made in 1926 by Paul Émile Appell with the help of Joseph Ser's development mentioned below. By calculating the continued fraction development of γ $\gamma$ (sequence A002852 in OEIS)

$\gamma =\left[0;1,1,2,1,2,1,4,3,13,5,1,1,8,1,2,4,1,1,40,1,11,3,7,1,7,1,1,5,1,49,4,1,65,1,4,7,11,1,399,2,1,3,2,1,2,1,5,3,2,1,\dotsc \right]$

lower bounds are obtained for positive integers and with γ $\gamma ={\tfrac {p}{q}}$ (for example, 475,006 denominators give the estimate $q>10^{244.663}$ ).

In contrast to square roots of rational numbers in the Pythagorean theorem and to the circle number π $\pi$ in the circumference and area of a circle with rational radius, Euler's constant does not occur in finite elementary geometric problems. However, there are many engineering problems that lead to the summation of the finite harmonic series $H_{n}$ , such as the centre of gravity problem of the cantilever or the problem of the optimal elevation of rows of seats in theatres and cinemas. Euler's constant appears in many problems in calculus, number theory and function theory and especially in special functions.

Convergence

The existence of Euler's constant results from the telescope sum

$\gamma =\lim _{n\rightarrow \infty }\left(\sum _{k=1}^{n}{\frac {1}{k}}-\ln(n+1)\right)=\sum _{k=1}^{\infty }\left({\frac {1}{k}}-\ln {\frac {k+1}{k}}\right).$

Since $\ln(n+1)-\ln(n)$ is a zero sequence, can be $\ln(n)$ used instead of $\ln(n+1)$ the defining limit. The following applies

${\frac {1}{k}}-\ln {\frac {k+1}{k}}={\frac {1}{k}}-\int _{k}^{k+1}{\frac {\mathrm {d} x}{x}}=\int _{k}^{k+1}{\frac {x-k}{xk}}\,\mathrm {d} x={\frac {1}{k}}\int _{0}^{1}{\frac {x}{x+k}}\,\mathrm {d} x.$

About

${\frac {1}{2(k+1)}}=\int _{0}^{1}{\frac {x}{1+k}}\,\mathrm {d} x\leq \int _{0}^{1}{\frac {x}{x+k}}\,\mathrm {d} x\leq \int _{0}^{1}{\frac {x}{k}}\,\mathrm {d} x={\frac {1}{2k}}$

therefore applies

${\frac {1}{2k\cdot (k+1)}}\leq {\frac {1}{k}}-\ln {\frac {k+1}{k}}\leq {\frac {1}{2k^{2}}}$

and thus the sum converges according to the major criterion.

In particular, it follows from this elementary argument and

$\sum _{k=1}^{\infty }{\frac {1}{k\cdot (k+1)}}=\sum _{k=1}^{\infty }\left({\frac {1}{k}}-{\frac {1}{k+1}}\right)=1$

and the Basel problem that

${\frac {1}{2}}\leq \gamma \leq {\frac {\pi ^{2}}{12}}$

applies.

The Euler-Mascheroni constant in mathematical problems

Euler's constant occurs frequently in mathematics and sometimes quite unexpectedly in various sub-areas. It mainly occurs in limit value processes of number sequences and functions as well as in limit values of differential and integral calculus. The occurrence can be subdivided (as with other mathematical constants) according to the type of limit value:

1. as a function value or limit value of special functions.

The value γ $\gamma$ is the negative of the derivative of the gamma function at the point 1, i.e.

$\Gamma ^{\prime }(1)=\psi (1)=-\gamma$ .

This gives the following limit representations, where $\zeta (s)$ denotes the Riemann zeta function and ψ $\psi (z)$ denotes the digamma function:

$\lim _{s\to 1}\left(\zeta (s)-{\frac {1}{s-1}}\right)=\gamma$

$\lim _{z\to 0}\left\{\Gamma (z)-{\frac {1}{z}}\right\}=\lim _{z\to 0}\left\{\psi (z)+{\frac {1}{z}}\right\}=-\gamma$

$\lim _{z\to 0}{\frac {1}{z}}\left\{{\frac {1}{\Gamma (1+z)}}-{\frac {1}{\Gamma (1-z)}}\right\}=2\gamma$

$\lim _{z\to 0}{\frac {1}{z}}\left\{{\frac {1}{\psi (1-z)}}-{\frac {1}{\psi (1+z)}}\right\}={\frac {\pi ^{2}}{3\gamma ^{2}}}$

2. in the development of special functions, e.g. in the series development of the integral logarithm of Leopold Schendel, the Bessel functions or the Weierstrass representation of the gamma function.

3. in the evaluation of certain integrals.

There is a rich abundance here, for example:

${\begin{aligned}\gamma &=-\int _{0}^{1}\ln(-\ln x)\,\mathrm {d} x\\\gamma &=-\int _{0}^{\infty }e^{-x}\ln x\,\mathrm {d} x\\\gamma &=\int _{0}^{\infty }\left({\frac {1}{e^{x}-1}}-{\frac {1}{xe^{x}}}\right)\,\mathrm {d} x\\\gamma &=\int _{0}^{1}\left({\frac {1}{\ln x}}+{\frac {1}{1-x}}\right)\,\mathrm {d} x\\\gamma &={\frac {1}{2}}+2\int _{0}^{\infty }{\frac {\sin(\arctan x)}{(e^{2\pi x}-1){\sqrt {1+x^{2}}}}}\,\mathrm {d} x\end{aligned}}$

or also

${\begin{aligned}\int _{0}^{\infty }e^{-x}\ln ^{2}x\,\mathrm {d} x&={\frac {\pi ^{2}}{6}}+\gamma ^{2}\\\int _{0}^{\infty }e^{-x^{2}}\ln x\,\mathrm {d} x&=-{\frac {\sqrt {\pi }}{4}}(\gamma +2\ln 2)\end{aligned}}$

There are also many invariant parameter integrals, e.g.:

${\begin{aligned}\gamma &=\int _{0}^{\infty }\left({\frac {1}{x^{k}+1}}-e^{-x}\right){\frac {\mathrm {d} x}{x}},\quad k>0\\\gamma &=\int _{0}^{\infty }\left({\frac {1}{kx+1}}-e^{-kx}\right){\frac {\mathrm {d} x}{x}},\quad k>0\end{aligned}}$

One can $\gamma$ also express γ as a double integral (J. Sondow 2003, 2005) with the equivalent series:

$\gamma =\int _{0}^{1}\int _{0}^{1}{\frac {x-1}{(1-xy)\ln(xy)}}\,\mathrm {d} x\,\mathrm {d} y=\sum _{n=1}^{\infty }\left({\frac {1}{n}}-\ln {\frac {n+1}{n}}\right)$ .

There is an interesting comparison (J. Sondow 2005) of the double integral and the alternating series:

$\ln \left({\frac {4}{\pi }}\right)=\int _{0}^{1}\int _{0}^{1}{\frac {x-1}{(1+xy)\ln(xy)}}\,\mathrm {d} x\,\mathrm {d} y=\sum _{n=1}^{\infty }(-1)^{n-1}\left({\frac {1}{n}}-\ln {\frac {n+1}{n}}\right)$ .

In this sense, we can say that $\ln {\big (}{\tfrac {4}{\pi }}{\big )}$ is the "alternating Euler's constant" (sequence A094640 in OEIS).

Furthermore, these two constants are linked to the pair

$\sum _{n=1}^{\infty }{\frac {N_{1}(n)+N_{0}(n)}{2n(2n+1)}}=\gamma ,$

$\sum _{n=1}^{\infty }{\frac {N_{1}(n)-N_{0}(n)}{2n(2n+1)}}=\ln \left({\frac {4}{\pi }}\right)$

of series, where $N_{1}(n)$ and are $N_{0}(n)$ the number of ones and zeros, respectively, in the binary expansion of (Sondow 2010).

Furthermore, there is an equally rich abundance of infinite sums and products, such as

${\begin{aligned}e^{\gamma }&=\lim _{n\to \infty }{\frac {1}{\ln n}}\prod _{p\leq n,p{\text{ prim}}}\left(1-{\frac {1}{p}}\right)^{-1}\\{\frac {6}{\pi ^{2}}}e^{\gamma }&=\lim _{n\to \infty }{\frac {1}{\ln n}}\prod _{p\leq n,p{\text{ prim}}}\left(1+{\frac {1}{p}}\right)\\\gamma &=\lim _{x\to 1^{+}}\sum _{n=1}^{\infty }\left({\frac {1}{n^{x}}}-{\frac {1}{x^{n}}}\right).\end{aligned}}$

4. as the limit value of series. The simplest example results from the limit value definition:

$\gamma =\sum _{n=1}^{\infty }\left({\frac {1}{n}}-\ln {\frac {n+1}{n}}\right)$ .

Series with rational terms come from Euler, Fontana and Mascheroni, Giovanni Enrico Eugenio Vacca, S. Ramanujan and Joseph Ser. There are countless variations on series with irrational members whose members consist of rationally weighted values of the Riemann zeta function at the odd argument positions ζ(3), ζ(5), .... An example of a particularly fast converging series is:

$\sum _{n=1}^{\infty }{\frac {\zeta (2n+1)-1}{(2n+1)2^{2n}}}=1+\ln 2-\ln 3-\gamma =$ 0.0173192269903...

Another series results from the Kummer series of the gamma function:

$\gamma =\ln \pi -4\ln \Gamma {\big (}{\tfrac {3}{4}}{\big )}+{\frac {4}{\pi }}\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {\ln(2k+1)}{2k+1}}$

Designations

One can say that Euler's constant is the constant with the most designations. Euler himself designated it with C and occasionally with O or n. However, it is doubtful whether he intended to introduce an independent symbol for his constant. Mascheroni did not designate the constant with γ - as is often claimed - but with A. The γ-misunderstanding stems from the article by J. W. L. Glaisher, which is often quoted without verification (although Glaisher explicitly notes there that he has not seen Mascheroni's book):

"Euler's constant (which throughout this note will be called γ after Mascheroni, De Morgan, &c.) [...]It
is clearly convenient that the constant should generally be denoted by the same letter. Euler used C and O for it; Legendre, Lindman, &c., C; De Haan A; and Mascheroni, De Morgan, Boole, &c., have written it γ, which is clearly the most suitable, if it is to have a distinctive letter assigned to it. It has sometimes (as in Crelle, t. 57, p. 128) been quoted as Mascheroni's constant, but it is evident that Euler's labours have abundantly justified his claim to its being named after him."

- J. W. L. Glaisher: On the history of Euler's constant, 1872, p. 25 and 30

Other mathematicians use the designations C, c, ℭ, H, γ, E, K, M, l. The origin of the designation γ used today is not certain. Carl Anton Bretschneider used the designation γ alongside c in an article written in 1835 and published in 1837, Augustus De Morgan introduced the designation γ in a textbook published in parts from 1836 to 1842 as part of his treatment of the gamma function.

Generalisations

Euler's constant knows several generalisations. The most important and best known is that of the Stieltjes constant:

$\gamma _{n}:=\lim _{N\to \infty }\left(\sum _{k=1}^{N}{\frac {\log ^{n}k}{k}}-{\frac {\log ^{n+1}N}{n+1}}\right),\quad n=0,1,2,\dotsc$

Number of calculated decimal places

In 1734, Leonhard Euler calculated six decimal places (five valid), later 16 places (15 valid). In 1790, Lorenzo Mascheroni calculated 32 decimal places (30 valid ones), of which, however, the three places 20 to 22 are wrong - apparently due to a clerical error, but they are given several times in the book. The error was the cause of several recalculations.

Number of published valid decimal places of γ
Date	Jobs	Author
1734	5	Leonhard Euler
1735	15	Leonhard Euler
1790	19	Lorenzo Mascheroni
1809	22	Johann Georg Soldner
1811	22	Carl Friedrich Gauss
1812	40	Friedrich Bernhard Gottfried Nicolai
1826	19	Adrien-Marie Legendre
1857	34	Christian Fredrik Lindman
1861	41	Ludwig Oettinger
1867	49	William Shanks
1871	99	J. W. L. Glaisher
1871	101	William Shanks
1877	262	John Couch Adams
1952	328	John William Wrench, Jr.
1961	1.050	Helmut Fischer & Karl Zeller
1962	1.270	Donald E. Knuth
1962	3.566	Dura W. Sweeney
1973	4.879	William A. Beyer & Michael S. Waterman
1976	20.700	Richard P. Brent
1979	30.100	Richard P. Brent & Edwin M. McMillan
1993	172.000	Jonathan Borwein
1997	1.000.000	Thomas Papanikolaou
1998	7.286.255	Xavier Gourdon
1999	108.000.000	Xavier Gourdon & Patrick Demichel
8 December 2006	116.580.041	Alexander J. Yee & Raymond Chan
18 January 2009	14.922.244.771	Alexander J. Yee & Raymond Chan
13 March 2009	29.844.489.545	Alexander J. Yee & Raymond Chan
22 December 2013	119.377.958.182	Alexander J. Yee
15 March 2016	160.000.000.000	Peter Trueb
18 May 2016	250.000.000.000	Ron Watkins
23 August 2017	477.511.832.674	Ron Watkins
26 May 2020	600.000.000.100	Seungmin Kim & Ian Cutress