Skip to content
Home

Euclidean space — n-dimensional Cartesian geometry and its properties

Mathematical setting for classical geometry: the n-dimensional Cartesian space with points, vectors, distance, and inner product. Origins in Euclid and Cartesian coordinates; used throughout science and engineering.

Author: Created: Updated:

Overview

Euclidean space is the standard mathematical model for classical, flat geometry. In practical terms it is the set of ordered n-tuples of real numbers, commonly written as Rn, whose elements represent points. Distances, angles and straight lines in this setting follow the familiar rules of plane and solid geometry. The study of these properties is classically called Euclidean geometry, whose early foundations appear in Euclid's Elements.

Image gallery

3 Images
Blender3D BW Grid 256
en.wikipedia.org · Public domain

Structure and basic properties

Formally, Euclidean space can be viewed as the vector space Rn together with an inner product that induces a norm and a metric. The inner product of two vectors defines lengths and angles, and the induced distance function d(x,y)=||x−y|| satisfies the familiar triangle inequality. Straight lines and planes are affine subspaces determined by linear equations or by a point and a direction. Isometries — transformations that preserve distances — include translations, rotations and reflections.

Key characteristics

  • Points as n-tuples: each point is an ordered list of n real coordinates.
  • Euclidean metric: length derived from the dot (inner) product.
  • Affine and vector structure: vectors represent directions and displacements.
  • Standard topology: open and closed sets, continuity and limits are the usual ones from Rn.

History and development

The ideas of Euclidean space trace to Euclid's axiomatic treatment of plane and solid geometry. Centuries later, René Descartes introduced Cartesian coordinates, which connected geometry with algebra and made the representation Rn commonplace. In the 19th and early 20th centuries geometers and logicians refined the axioms and clarified the distinction between Euclidean and non-Euclidean geometries; modern treatments place Euclidean space within the frameworks of linear algebra, metric spaces and manifold theory.

Uses, examples and importance

Euclidean space underlies much of applied mathematics and the physical sciences. Examples include the plane R2 for maps and drawings, the physical space R3 used in mechanics and optics, and higher-dimensional Rn in statistics, optimization, and data analysis. Calculus on Rn provides multivariable derivatives and integrals; linear algebra describes transformations and coordinates. Computer graphics, robotics, and engineering rely on Euclidean notions of distance and orientation.

Distinctions and notable facts

Euclidean space is "flat" in the sense that its geometry obeys the parallel postulate; this contrasts with curved geometries such as spherical or hyperbolic spaces. It is a specific example of an inner product space and an affine space, but not every affine or metric space is Euclidean. For rigorous foundations one can study axiomatic systems that characterize Euclidean geometry; these clarify which properties depend on particular axioms and which follow from algebraic structure alone. For further background see discussions of three-dimensional space and axiomatic treatments in modern texts: 3D Euclidean space and axiomatic foundations.

Euclidean vector spaces

See also: Scalar product space

From Euclidean visual space to Euclidean vector space

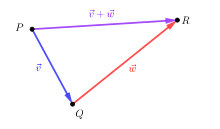
In analytic geometry, one associates a vector space with Euclidean space. One way to do this is to take the set of parallel displacements (translations), provided with the one behind the other as an addition. Each translation can be described by an arrow connecting a point to its image point. Two arrows, which are parallel in the same direction and have the same length, describe the same displacement. Two such arrows are called equivalent and the equivalence classes are called vectors.

If one chooses a point Oas reference point (origin) in the Euclidean space, one can assign to{\vec {p}}={\overrightarrow {OP}} each point Pits location vector , the vector Prepresented by an arrow from the origin Oto the point In this way, one gets a one-to-one relationship between the Euclidean space and the associated Euclidean vector space, and can thus identify the original Euclidean space with the Euclidean vector space. However, this identification is not canonical, but depends on the choice of the origin.

One can now also transfer the length and angle measurement from Euclidean space to vectors as the length of the associated arrows and angles between such. In this way one obtains a vector space with scalar product. The scalar product is characterized by the fact that the product {\vec {a}}\cdot {\vec {a}}a vector {\vec {a}}with itself |{\vec {a}}|gives the square |{\vec {a}}|^{2}its length From the laws of arithmetic for scalar products, the binomial formulas, and the cosine theorem (applied to a triangle whose sides correspond to vectors {\vec {a}}, {\vec {b}}and {\vec {b}}-{\vec {a}}), we obtain the formula

{\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\,|{\vec {b}}|\,\cos \sphericalangle ({\vec {a}},{\vec {b}}).

Here denotes \sphericalangle ({\vec {a}},{\vec {b}})the angle between vectors {\vec {a}}and {\vec {b}}.

General term

Starting from this, any real vector space with scalar product (of arbitrary finite dimension n) is called a Euclidean vector space. One then uses the above formula to define length (norm) of a vector and angles between vectors. Two vectors are orthogonal if their scalar product is zero. Every three-dimensional Euclidean vector space is isometrically isomorphic to the vector space of arrow classes. Every n-dimensional Euclidean vector space is isometrically isomorphic to the coordinate vector space \mathbb {R} ^{n}(see below). Euclidean vector spaces of the same dimension nare thus indistinguishable. This entitles one to call any such one the Euclidean vector space of dimension . nSome authors use the term Euclidean space also for infinite-dimensional real vector spaces with scalar product, some also for complex vector spaces with scalar product, cf. scalar product space.

Lengths, angles, orthogonality and orthonormal bases

See also: Orthonormal basis

Once one has provided a real vector space with a scalar product, one can transfer the metric notions of the Euclidean visual space to it. The length (the norm, the magnitude) of a vector {\vec {a}}is then the square root of the scalar product of the vector with itself:

|{\vec {a}}|={\sqrt {{\vec {a}}\cdot {\vec {a}}}}.

Two vectors {\vec {a}},{\vec {b}}are orthogonal (or perpendicular) to each other if their scalar product is zero:

{\vec {a}}\perp {\vec {b}}\Leftrightarrow {\vec {a}}\cdot {\vec {b}}=0.

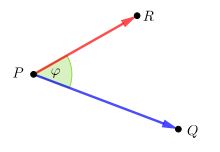
The (non-oriented) angle between two vectors is defined by the above formula

{\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\,|{\vec {b}}|\,\cos \sphericalangle ({\vec {a}},{\vec {b}}),

Sync and corrections by n17t01

\sphericalangle ({\vec {a}},{\vec {b}})=\arccos {\frac {{\vec {a}}\cdot {\vec {b}}}{|{\vec {a}}|\,|{\vec {b}}|}}.

A vector {\vec {a}}is called a unit vector if it has length 1. A basis of unit vectors that are pairwise orthogonal is called an orthonormal basis. Orthonormal bases exist in every Euclidean vector space. If {\vec {e}}_{1},\dotsc ,{\vec {e}}_{n}is an orthonormal basis, then the vector {\vec {a}}represented in this basis:

{\displaystyle {\vec {a}}=a_{1}{\vec {e}}_{1}+\dotsb +a_{n}{\vec {e}}_{n}}.

The coefficients are obtained by

a_{i}={\vec {a}}\cdot {\vec {e}}_{i}.

Isometrics

If Vand are Wtwo n -dimensional Euclidean vector spaces, then a linear mapping is called f\colon V\to Wa (linear) isometry if it preserves the scalar product, i.e. if

f({\vec {a}})\cdot f({\vec {b}})={\vec {a}}\cdot {\vec {b}}

{\vec {a}},{\vec {b}}\in Vholds for all Such a mapping f is also called an orthogonal mapping. In particular, an isometry preserves lengths

|f({\vec {a}})|=|{\vec {a}}|

and angles, i.e. in particular orthogonality

f({\vec {a}})\perp f({\vec {b}})\Longleftrightarrow {\vec {a}}\perp {\vec {b}}.

Conversely, any linear mapping that preserves lengths is an isometry.

An isometry maps every orthonormal basis back to an orthonormal basis. Conversely, if {\vec {e}}_{1},\dotsc ,{\vec {e}}_{n}is an orthonormal basis of Vand {\vec {e}}_{1}{}',\dotsc ,{\vec {e}}_{n}{}'an orthonormal basis of W, then there is exactly one isometry that {\vec {e}}_{i}{}'maps {\vec {e}}_{i}to

From this it follows that two Euclidean vector spaces of the same dimension are isometric, that is, they are indistinguishable as Euclidean vector spaces.

Two points and their position vectors
Two points and their position vectors
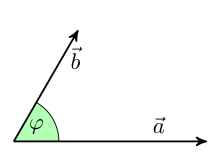
Angle between two vectors
Angle between two vectors

The Euclidean point space

Motivation

Euclidean vector spaces often serve as models for Euclidean space. The elements of the vector space are then called points or vectors, depending on the context. No distinction is made between points and their location vectors. Computationally, this can be advantageous. Conceptually, however, it is unsatisfactory:

  • From a geometric point of view, points and vectors should be distinguished conceptually.
    • Vectors can be added and multiplied by numbers, but points cannot.
    • Points are connected or merged by vectors.
  • In the vector space there is a distinguished element, the zero vector. But in Euclidean geometry all points are equal.

Description

The remedy is the concept of a Euclidean point space. This is an affine space over a Euclidean vector space. Here one distinguishes between points and vectors.

  • The totality of points forms the Euclidean point space. This is usually denoted by E, E_{n}, E^{n}or ^{n}} (The superscript \mathbb {E} ^{n}nis not an exponent, but an index denoting the dimension. So E^{n}is not a Cartesian product).
  • The set of all vectors forms a Euclidean vector space V.
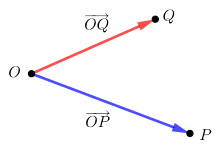
  • For every two points Pand Q\in E
     there exists exactly one connection vector, denoted by     {\overrightarrow {PQ}}
    . The connection vector of a point with itself is the zero vector:
     {\overrightarrow {PP}}={\vec {0}}
  • A point Pcan be uniquely Qtransformed into a point {\vec {v}} by a vector This is often denoted by P+{\vec {v}}. (This is a purely formal notation. The plus sign does not denote vector space addition, nor addition on the point space.)
    The zero vector merges every vector into itself:     P+{\vec {0}}=P
  • If the vector {\vec {v}} passes the point Pto the point Q and the vector {\vec {w}} passes the point Qto the point R, then {\vec {v}}+{\vec {w}} Rtransits the point P into the point This can be expressed as follows:

(P+{\vec {v}})+{\vec {w}}=P+({\vec {v}}+{\vec {w}})

{\overrightarrow {PQ}}+{\overrightarrow {QR}}={\overrightarrow {PR}}

In the language of algebra, these properties mean: The additive group of the vector space Voperates freely and transitively on the set E.

Lengths, distances and angles

Line lengths, distances between points, angles and orthogonality can now be defined using the scalar product of vectors:

The length {\overline {PQ}}of the line [PQ]and the distance d(P,Q)the points Pand Qis defined as the length of the vector {\overrightarrow {PQ}}:

{\displaystyle d(P,Q)={\overline {PQ}}=|{\overrightarrow {PQ}}|}

The size of the angle \sphericalangle QPRis defined as the angle between the vectors {\overrightarrow {PQ}}and {\displaystyle {\overrightarrow {PR}}}:

\sphericalangle QPR=\sphericalangle ({\overrightarrow {PQ}},{\overrightarrow {PR}})

Two distances [PQ]and [RS]are orthogonal if and only if the associated vectors {\overrightarrow {PQ}}and {\overrightarrow {RS}}orthogonal.

Images

Length-preserving mappings of a Euclidean point space to itself are called isometries, congruence mappings (in plane geometry), or motions. They automatically preserve angles as well. If f\colon E\to Ea motion, then there exists an orthogonal mapping (linear isometry) {\vec {f}}\colon V\to V, such that for all points Pand Qholds:

f(Q)=f(P)+{\vec {f}}({\overrightarrow {PQ}})

The angle \sphericalangle QPRis the angle between the vectors \textstyle {\overrightarrow {PQ}}and \textstyle {\overrightarrow {PR}}

Related articles

Author

AlegsaOnline.com Euclidean space — n-dimensional Cartesian geometry and its properties

URL: https://en.alegsaonline.com/art/32466

Share

Sources