Errors and residuals

This article is about the statistical point of view. For a numerical view, see Residual (Numerical Mathematics).

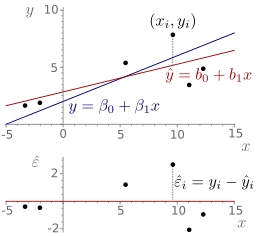
In statistics, confounding variables and residuals are two closely related concepts. The disturbance variables (not to be confused with disturbance parameters or disturbance factors), also called disturbance variables, disturbance terms, error terms, or errors for short, are unobservable random variables in a simple or multiple regression equation that measure the vertical distance between the observation point and the true straight line (regression function of the population). They are usually assumed to be uncorrelated, to have an expected value of zero and to have a homogeneous variance (Gauss-Markow assumptions). They include unobserved factors that affect the dependent variable. The confounding variable may also include measurement error in the observed dependent or independent variables.

In contrast to the disturbance variables, residuals (Latin residuum = "the one left behind") are calculated variables and measure the vertical distance between the observation point and the estimated regression line. Sometimes the residual is also referred to as the "estimated residual". This naming is problematic because the confounding variable is a random variable and not a parameter. It is therefore not possible to speak of an estimate of the disturbance variable.

The problem with the so-called regression diagnostics is that the Gauss-Markow assumptions only refer to the disturbance variables, but not to the residuals. Although the residuals also have an expected value of zero, they are not uncorrelated and do not exhibit a homogeneous variance. To account for this shortcoming, the residuals are usually modified to meet the required assumptions, e.g. studentized residuals. The sum of squares of the residuals plays a major role in statistics in many applications, e.g., in the least squares method. The notation of the disturbance variables as ε $\varepsilon_i$ or is $e_{i}$ adapted from the Latin word erratum (error). The residuals can be generated using the residual matrix.

Theoretical true straight line and estimated regression straight line ${\hat {y}}$ . The residual ε ${\hat {\varepsilon }}_{i}$ is the difference between the measured value $y_{i}$ and estimated value $\hat{y}_i$ .

Disturbance and residual

Disturbance variables are not to be confused with residuals. One distinguishes the two concepts as follows:

Unobservable random perturbations ε $\varepsilon_i$ : measure the vertical distance between observation point and theoretical (true straight line).
Residual ε ${\hat {\varepsilon }}_{i}=y_{i}-{\hat {y}}_{i}$ : Measure the vertical distance between empirical observation and the estimated regression line.

Simple linear regression

→ Main article: Linear simple regression

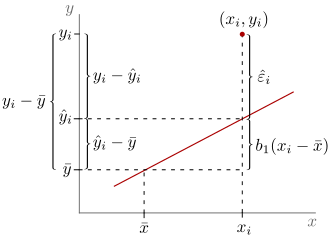
In the simple linear regression with the single linear regression model the ordinary residuals $Y_{i}=\beta _{0}+\beta _{1}x_{i}+\varepsilon _{i}$ are given by

${\hat {\varepsilon }}_{i}=y_{i}-{\hat {y}}_{i}=y_{i}-{\hat {\beta }}_{0}-{\hat {\beta }}_{1}x_{i}$ .

These are residuals, since an estimated value is subtracted from the true value. More precisely, the fitted values are subtracted from the observed values y_{i}} $y_{i}$ ${\hat {y}}_{i}={\hat {\beta }}_{0}+{\hat {\beta }}_{1}x_{i}$ . In simple linear regression, numerous assumptions are usually made on the confounding variables (see Assumptions about confounding variables).

Residual variance

(also called residual variance) is an estimate of the variance of the regression function in the population $\operatorname {Var} (y\mid X=x)=\operatorname {Var} (\beta _{0}+\beta _{1}x+\varepsilon )=\sigma ^{2}=\operatorname {konst}$ . In simple linear regression, an estimate found by maximum likelihood estimation is given by.

${\tilde {s}}_{\varepsilon }^{2}={\frac {1}{n}}\sum \limits _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}={\frac {1}{n}}\sum \limits _{i=1}^{n}(y_{i}-{\hat {\beta }}_{0}-{\hat {\beta }}_{1}x_{i})^{2}$ .

However, the estimator does not meet common quality criteria for point estimators and is therefore not often used. For example, the estimator is not expectation-true for σ $\sigma ^{2}$ . In simple linear regression, under the assumptions of the classical model of linear simple regression, it can be shown that an expectation-true estimate of the variance of the confounding variables σ $\sigma ^{2}$ , i.e. .an estimate that $\operatorname {E} ({\hat {\sigma }}^{2})=\sigma ^{2}$ is satisfied, given by the variant adjusted for the number of degrees of freedom:

${\hat {\sigma }}^{2}={\frac {1}{n-2}}\sum \limits _{i=1}^{n}(y_{i}-{\hat {\beta }}_{0}-{\hat {\beta }}_{1}x_{i})^{2}$ .

The positive square root of this expectation-stratified estimator is also referred to as the standard error of the regression.

Residuals as a function of the disturbance variables

In simple linear regression, the residuals as a function of the confounding variables ε $\varepsilon_i$ for each individual observation can be written as

${\hat {\varepsilon }}_{i}=\varepsilon _{i}-({\hat {\beta }}_{0}-\beta _{0})-({\hat {\beta }}_{1}-\beta _{1})x_{i}$ .

Sum of the residuals

The KQ regression equation is determined so that the residual sum of squares becomes a minimum. Equivalently, this means that positive and negative deviations from the regression line balance each other out. If the model of the linear single regression contains a - non-zero - intercept, then it must therefore hold that the sum of the residuals is zero

$\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}=0$

This graph shows the decomposition of the "variance to be explained" $\left(y_{i}-{\overline {y}}\right)$ into the "explained variance" $\left({\hat {y}}_{i}-{\overline {y}}\right)$ and the "residual" $\left(y_{i}-{\hat {y}}_{i}\right)$ .

Questions and Answers

Q: What is meant by statistical errors and residuals?

A: Statistical errors and residuals refer to the difference between the observed or measured value and the real value, which is unknown.

Q: How can one measure accuracy of a measurement?

A: One can measure the same thing again and again, and collect all the data together. This allows us to do statistics on the data in order to determine how accurate a measurement is.

Q: What is an example of a statistical error?

A: An example of a statistical error would be if there was an experiment to measure the height of 21-year-old men from a certain area with an expected mean of 1.75m, but one man chosen at random was 1.80m tall; then the "(statistical) error" would be 0.05m (5cm).

Q: What is an example of a residual?

A: An example of a residual would be if there was an experiment to measure the height of 21-year-old men from a certain area with an expected mean of 1.75m, but one man chosen at random was 1.70m tall; then the residual (or fitting error) would be -0.05m (-5cm).

Q: Are residuals independent variables?

A: No, The sum of the residuals within a random sample must be zero so they are not independent variables.

Q: Are statistical errors independent variables?

A: Yes, The sum of the statistical errors within a random sample need not be zero; therefore they are independent random variables if individuals are chosen from population independently.

Q: Is it possible to do exact measurements?

A:No, it is not possible to do exact measurements because measurement is never exact