Epigraph (mathematics)

In mathematics, the epigraph of a real-valued function $f\colon X\to \mathbb {R}$ the set of all points lying on or over its graph.

$\operatorname {epi} f:=\left\{(x,\mu )\in X\times \mathbb {R} \,:\,f(x)\leq \mu \right\}\subseteq X\times \mathbb {R}$

If the image space of the function of $\mathbb {R} ^{n}$ provided with a generalized inequality $\preccurlyeq _{K}$ , the epigraph is defined as

Properties

Let be a normalized $\mathbb {R}$ -vector space. For functions $f\colon X\rightarrow {\mathbb {R}}$ holds:

is convex if and only if the epigraph of forms a convex set.
is semi-continuous from below if and only if the epigraph of forms a closed set.
is weakly inferior if and only if the epigraph of is a weakly sequence-terminated set.
If an affine-linear function, then its epigraph defines a half-space in .

If the image space of the function of is $\mathbb {R} ^{n}$ , then it is K-convex if and only if the epigraph is convex.

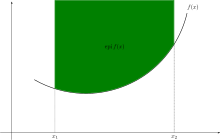
The epigraph of a convex function is a convex set