Enthalpy

The enthalpy (ancient Greek ἐν en 'in' and θάλπειν thálpein 'to heat'), formerly also heat content, of a thermodynamic system is the sum of the internal energy the system and the product of pressure and volume } of the system:

H=U+pV .

It has the dimension of energy and is measured in the unit joule.

Enthalpy is an extensive quantity: The enthalpy of a total system is the sum of the enthalpies of the subsystems.

The molar enthalpy (unit: J/mol) is the enthalpy related to the amount of substance

$H_{\mathrm {m} }={\frac {H}{n}}$ .

The specific enthalpy (unit: J/kg) is the enthalpy related to the mass

$h={\frac {H}{m}}$ .

The molar and specific enthalpies are intensive quantities: If two identical subsystems have the same molar or specific enthalpy, then the total system formed from them also has this molar or specific enthalpy.

The enthalpy is, like , and a state variable; it is uniquely determined by the current state of the system and is independent of the previous history of the system.

The practical usefulness of the enthalpy calculation parameter is based on the fact that the change in the enthalpy of a system caused by a process is

$\mathrm {d} H=\mathrm {d} (U+p\ V)=\mathrm {d} U+p\ \mathrm {d} V+V\ \mathrm {d} p$

by the simpler expression

$\mathrm {d} H=\mathrm {d} U+p\ \mathrm {d} V$

if the process takes place at constant pressure (isobaric, $\mathrm {d} p=0$ ). However, this expression can be interpreted as the "gross energy" that must be supplied to the system if its internal energy is to be increased by the amount $\mathrm {d} U$ and the system $p\,\mathrm {d} V$ consumes part of the supplied energy for the volume change work performed during the process. In the case of an isobaric process, one can therefore $\mathrm{d}H$ identify the "gross energy" to be expended $\mathrm {d} U+p\ \mathrm {d} V$ with the enthalpy and use the advantages offered by calculating with state variables. If the system does not perform any other form of work besides the volume change work, the enthalpy conversion of the process is equal to the heat conversion.

Numerous physical and chemical processes take place at constant pressure. This is often the case, for example, with phase transitions or chemical reactions, especially (but not only) when they take place under atmospheric pressure. The enthalpy is then a suitable quantity for describing the heat conversion of these processes.

In theoretical thermodynamics, enthalpy is a fundamental function from which the entire thermodynamic information about the system can be derived. However, the prerequisite is that it is a function of the variables entropy , pressure and mole numbers $N_{i}$ the chemical components contained in the system. These are the "natural variables" of enthalpy. It can also be set as a function of other variables, but then no longer contains the complete thermodynamic information.

The enthalpy is a Legendre transform of the internal energy. The internal energy is also a fundamental function if it is expressed as a function of its natural variables , , $N_{i}$ is given. The transition to other sets of variables requires the application of a Legendre transformation if it is to be done without loss of information. The transformation that creates a fundamental function from the internal energy with the natural variables , , $N_{i}$ yields the expression $U+p\ V$ , i.e. the enthalpy. The additive term following from the Legendre transformation $p\ V$ compensates for the loss of information that would otherwise be associated with the change of variable.

To be distinguished from enthalpy is free enthalpy or Gibbs energy, the Legendre transformation of enthalpy after entropy.

The enthalpy of reaction of the combustion of alcohol in air is negative. It is therefore an exothermic reaction in which heat is released into the environment.

The melting enthalpy is the amount of energy required to melt the ice at constant pressure. It is extracted from the environment and cools the drink in the process.

Enthalpy in isobaric physical and chemical processes

Numerous processes from physics (e.g. phase transitions) or from chemistry (e.g. chemical reactions) take place under constant pressure. In these cases, the enthalpy allows a simple description and calculation of the heat conversion.

Standard enthalpy of formation

As already mentioned, any process that connects the two states can be used to calculate the enthalpy difference between two states. For example, in a chemical reaction, one can mentally break down the starting materials into their elements and reassemble them into the product materials. The enthalpy to be expended or dissipated in each case is the so-called enthalpy of formation of the substance in question. The enthalpies of formation depend on temperature and pressure. The enthalpies of formation that are converted under standard conditions are the standard enthalpies of formation.

The molar standard enthalpy of formation (usually abbreviated to standard enthalpy of formation) is the enthalpy that is released (negative sign) or required (positive sign) for the formation of one mole of a substance from the allotropically most stable form of the pure elements under standard conditions (100 kPa and 25 °C). It is usually expressed in kilojoules per mole. The quantity is formulated Δ $\Delta H_{f}^{0}$ ( from English formation stands for formation; the superscript zero for standard conditions; the delta for the difference). An alternative notation is Δ $\Delta H_{B}^{0}$ ( from German Bildung), the German spelling.

If it is negative, it is an exothermic reaction and energy is released during the formation of the substance from the elements (heat of formation). If, on the other hand, it is positive, it is an endothermic reaction and energy must be expended to form the substance from its initial elements. Strongly negative values of the standard enthalpy of formation are a characteristic of chemically particularly stable compounds (i.e. a lot of energy is released during their formation and a lot of energy must be expended to destroy the bonds). The standard enthalpy of formation of the chemical elements in their most stable state (H2, He, Li, ...) is set to 0 kJ/mol by definition.

If the standard enthalpies of formation of the substances involved in a chemical reaction are known, the enthalpy of reaction of this reaction under standard conditions can be easily calculated. It is the difference between the standard enthalpies of formation of the reaction products on the one hand and the starting materials (reactants; "reactants") on the other (Hess theorem):

$\Delta H_{\mathrm {Reaktion} }^{0}=\sum \Delta H_{f,\mathrm {Produkte} }^{0}-\sum \Delta H_{f,\mathrm {Edukte} }^{0}$

All values refer to thermodynamic equilibrium, otherwise the temperature would not be defined.

Conversely, the standard enthalpy of formation can be determined with the help of Hess' theorem from enthalpies of reactions in which the respective substance participates as a reactant or product. If no experimental data are available, an estimation of the standard enthalpies of formation can also be estimated using group contribution methods. The increment method according to Benson is particularly suitable for this.

Inorganic substances

Chemical formula	Fabric	$\Delta H_{f}^{0}$ (kJ/mol)	Source
H2O (g)	Water (gaseous)	−241,83
H2O (l)	Water (liquid)	−285,83
_CO2 (g)	Carbon dioxide	−393,50
NH3 (g)	Ammonia	−45,94

Organic substances

Sum formula	Fabric	$\Delta H_{f}^{0}$ (kJ/mol)	Source
CH4 (g)	Methane	−74,87
_C2H4 (g)	Ethylene	+52,47
_C2H6 (g)	Ethan	−83,8

Enthalpy in physics (thermodynamics)

In a narrower sense, thermodynamics describes only the intermolecular forces, i.e. the energetic relationships (phase states or their changes) between the individual molecules of a substance.

Enthalpy of evaporation / enthalpy of condensation

→ Main article: Heat of evaporation

The molar enthalpy of vapourisation Δ $\Delta _{V}H$ the enthalpy required to bring one mole of a substance isothermally and isobarically from the liquid to the gaseous state. The enthalpy of vapourisation depends on the substance as well as on temperature and pressure, although it is always positive and its sign is therefore not usually given.

The molar enthalpy of condensation Δ $\Delta _{K}H$ is the enthalpy that is released when one mole of a substance condenses, whereby it again changes isothermally and isobarically from the gaseous to the liquid state of aggregation. It always carries a negative sign.

The enthalpy of vapourisation decreases with increasing temperature and becomes zero when the critical point is reached, as it is no longer possible to distinguish between liquid and gas there. As a rule, in tabular works, enthalpy of vaporisation data are either related to 25 °C or tabulated for the various temperature-pressure combinations along the boiling point curve, it always applies Δ $\Delta _{V}H=-\Delta _{K}H$ .

For mixtures or solutions of substances, the enthalpies add up in the ratio of their mixture proportions.

If no enthalpy of vapourisation values are available for a substance, these can be calculated for any temperature with the help of the Clausius-Clapeyron equation if the temperature dependence of the vapour pressure curve is known at the temperature under consideration.

In rare cases, values for enthalpies of vaporisation were tabulated. The enthalpy of vaporisation can always be derived from the thermodynamic data by difference formation if standard enthalpy of formation values for the liquid and gaseous state of aggregation are known, e.g. for water, carbon disulphide, methanol, ethanol, formic acid, acetic acid, bromine in the table above.

Take table salt, for example:

Evaporation enthalpy ∆VH = +170 kJ/mol (at 1465 °C, table value)
For the practical calculation of the heat of evaporation, the following table values for the enthalpy of formation are used:

NaCl (melt)	$\longrightarrow$	NaCl (g)
-386 kJ/mol		-182 kJ/mol	Formation enthalpies (25 °C)
$\Rightarrow$ Evaporation enthalpy ∆VH = +204 kJ/mol

The difference between the two values 170 and 204 is within the usual range.

Enthalpy of sublimation

Sublimation describes the transition of a solid into the gas phase bypassing the liquid melt phase (technical application in freeze-drying). The enthalpy of sublimation is sometimes listed in tables. In principle, the enthalpy of fusion and the enthalpy of evaporation may also be combined at the same reference temperature:

Enthalpy of sublimation = enthalpy of fusion + enthalpy of evaporation.

The enthalpy of sublimation should not be confused with the heat of sublimation. This corresponds to the sum of the heat of fusion and the heat of evaporation.

The enthalpy of sublimation can always be derived from the thermodynamic data if standard enthalpy of formation values for the solid and gaseous states of aggregation are known.

Sublimation enthalpy of common salt: 211 kJ/mol (25 °C, table value)
Calculation:

NaCl (s)	$\longrightarrow$	NaCl (g)
-411 kJ/mol		-182 kJ/mol	Formation enthalpies (25 °C)
$\Rightarrow$ sublimation enthalpy +229 kJ/mol

Note: The example shows that in principle one can also calculate processes that are hardly feasible in practice. The "sublimation enthalpy of elemental carbon" was "determined" in this way.

Sublimation enthalpies of some substances
Fabric sign	Fabrics	Enthalpy of sublimation (kJ/mol)	Standard enthalpy of formation (solid) (KJ/mol)	Standard enthalpy of formation (gas) (KJ/mol)
Na	Sodium	108,7	0,0	108,7
K	Potassium	90,0	0,0	90,0
Br2	Bromine	30,71	0,0	30,71
Li	Lithium	155,10	0,0	155,10
I2	Iodine	62,4
C10H8	Naphthalene	72,6
_CO2	Carbon dioxide	26,1

Enthalpy of fusion / enthalpy of crystallisation

After heating a solid substance to its melting point temperature, heat of fusion is absorbed at this temperature without the temperature rising any further. This form of heat is called latent heat because it does not cause a change in temperature. In the case of ionic solids, the phase transformation solid/liquid results in salt melts with easily movable ions (technical application in fused-salt electrolysis). Table salt melts at 800 °C.

Melting halpies are rarely recorded in tables.

The enthalpy of fusion can always be derived from the thermodynamic data if standard enthalpy of formation values for the solid and liquid states of aggregation are known.

Melting enthalpy of common salt: 28; 30.2 kJ/mol (800 °C, table values)
For practical calculation of the heat of fusion, the following table values are used:

NaCl (s)	$\longrightarrow$	NaCl (melt)
-411 kJ/mol		-386 kJ/mol			Formation enthalpies (25 °C)
NaCl (s)	$\longrightarrow$	Na+ (melt)	+	Cl- (melt)
-411 kJ/mol		approx. -215 kJ/mol		approx. -170 kJ/mol	Formation enthalpies (25 °C)
$\Rightarrow$ Melting enthalpy +25 kJ/mol (NaCl, 25 °C)

In the reversal of this process, crystallisation from the melt, the ions of a salt can combine directly to form their solid crystal lattice. During the precipitation of common salt crystals from the melt, -25.2 kJ/mol enthalpy of crystallisation (or 29±1 kJ/mol at 800 °C) is released.

Experience shows that "supercooled molten salts" can release considerable amounts of heat due to spontaneous crystallisation. (Application: heating pad).

Lattice enthalpy

According to a common definition, the lattice energy is the energy that must be expended in a vacuum (i.e. at external pressure p=0 ) to convert a crystalline ionic solid into the gas phase (i.e. sublimation energy), i.e. to separate it into the gaseous ions. The lattice energy and the lattice enthalpy differ qualitatively. The lattice energy is an internal energy, while the lattice enthalpy is an enthalpy. The lattice enthalpy therefore additionally takes into account the volume work $p\Delta V$ be performed against a constant external pressure. If one has determined a molar lattice enthalpy Δ $\Delta _{G}H$ for the separation of the components of the solid, then the molar lattice energy Δ $\Delta _{G}U=\Delta _{G}H-p\Delta V_{\mathrm {m} }$ . Here Δ $\Delta V_{{\mathrm {m}}}$ the volume change related to the amount of substance.

The lattice enthalpy of NaCl is composed as follows:

NaCl (solid)	$\longrightarrow$	Na+ (g)	+	Cl- (g)
-411 kJ/mol		611 kJ/mol		-244 kJ/mol	Formation enthalpies (25 Â°C)
$\Rightarrow$ Lattice enthalpy +778 kJ/mol

Comparison: This is approximately twice the necessary energy that would be released in the strongly exothermic reaction of sodium metal and chlorine gas. The formation of gaseous ions is therefore extremely endothermic.

The lattice enthalpy ΔH0L depends on the size and charge of the ions involved and is always positive in this type of definition, otherwise the lattice would not be stable. Aluminium oxide Al2O3 (Al3+ and O2-) has a very high lattice enthalpy of 15157 kJ/mol. The high lattice enthalpy is exploited in aluminothermic processes; these include aluminothermic welding and the preparation of elements from their oxides and aluminium by means of aluminothermy. In the latter case, the high lattice enthalpy of the aluminium oxide is a main driving force for the reaction, as it is directly reflected in the Gibbs energy.

The lattice energy is often also defined as the enthalpy of reaction in the formation of the solid salt lattice starting from ions in the gas phase. If the lattice energy is defined in this way, the process is exothermic and the associated enthalpy change must be given as negative. The lattice enthalpy of aluminium oxide would then be -15157 kJ/mol, for example.

The lattice enthalpy depends on the size of the ions involved: The larger the ions, the smaller the lattice energy released, since the attractive forces decrease with increasing distance of the positive nuclei from the negative electron shell of the bonding partner.

Examples: Molar lattice enthalpy of alkali fluorides at 25 °C in kJ/mol:

Name	Formula	Ion radius of the monovalent alkali metal cations X+ in pm	Lattice enthalpy in kJ per mol
Lithium fluoride	LiF	74	1039
Sodium fluoride	NaF	102	920
Potassium fluoride	KF	138	816
Rubidium fluoride	RbF	149	780
Caesium fluoride	CsF	170	749

On the other hand, the lattice energy depends on the electrical charge of the ions involved: The greater the charges, the greater the attractive forces and the greater the lattice energy.

Examples: molar lattice enthalpy at 25 °C in kJ per mol (in the examples, the ion radius changes only slightly):

Name	Formula	Cations	Anions	Lattice enthalpy in kJ per mol
Sodium chloride	NaCl	Na+	Cl-	780
Sodium sulphide	Na2S	Na+	^S2−	2207
Magnesium chloride	MgCl2	Mg2+	Cl-	2502
Magnesium sulphide	MgS	Mg2+	^S2−	3360

For a similar effect with graphite under neutron irradiation, see Wigner energy.

Solvation enthalpy, hydration enthalpy

It indicates the energy released when gaseous ions attach to solvents, i.e. form solvated ions. For the most frequent case of solvent = water, one speaks of enthalpy of hydration.

Na+ (g)	$\longrightarrow$	Na+ (hydrated)
611 kJ/mol		-240 kJ/mol	Formation enthalpies (25 Â°C)
$\Rightarrow$ Hydration enthalpy Na+ -851 kJ/mol (i.e. extremely exothermic)

Cl- (g)	$\longrightarrow$	Cl- (hydrated)
-244 kJ/mol		-167 kJ/mol	Formation enthalpies (25 Â°C)
$\Rightarrow$ Hydration enthalpy Cl- +77 kJ/mol (i.e. weakly endothermic)

The hydration enthalpy of the gaseous ions of common salt is strongly exothermic with -774 kJ/mol overall.

Enthalpy of solution / enthalpy of crystallisation

The enthalpy of solution of salts involves 1) the separation of the ion lattice into single ions and 2) the solvation of the single ions. Sub-step 1) is very strongly endothermic, sub-step 2) very strongly exothermic.

Solution enthalpy = lattice enthalpy + solvation enthalpy.

Solution enthalpy NaCl in water = (+778 kJ/mol) + (-851+77 kJ/mol) = +4 kJ/mol (25 °C).

This value is in good agreement with table works +3.89 kJ/mol for the saline heat of dissolution. Thus, a very slight cooling of the solution occurs during dissolution.

Of course, for practical calculations of the heat of solution one does not take the diversions via the lattice energy, but one calculates directly and with only a few table values (occasionally one finds the value (NaCl)hydrat. = -407 kJ/mol instead of the individual ions):

NaCl (s)	$\longrightarrow$	NaCl (hydrated)
-411 kJ/mol		-407 kJ/mol			Formation enthalpies (25 Â°C)
NaCl (s)	$\longrightarrow$	Na+ (hydrated)	+	Cl- (hydrated)
-411 kJ/mol		-240 kJ/mol		-167 kJ/mol	Formation enthalpies (25 Â°C)
$\Rightarrow$ Solution enthalpy +4 kJ/mol (water, 25 °C)

The enthalpy of solvation can always be derived from the thermodynamic data if one finds standard enthalpy of formation values for the solid and dissolved state of aggregation, e.g. formic acid and carbon dioxide in the table above. It applies to "infinite dilution".

When this process is reversed, crystallisation from solution, the dissolved ions of a salt 1) release their solvate shell and 2) join together in a solid crystal lattice. During the precipitation of common salt crystals from water, -3.89 kJ/mol enthalpy of crystallisation is released.

Intermolecular enthalpy contributions

Differently strong interactions between the molecules are the reason why groups of substances have similar or very different enthalpies of sublimation.

Weak contributions are provided by London forces, dipole-dipole interactions and ion-dipole interactions with 1-15 kJ/mol binding. They are summarised as Van der Waals interactions. See the melting and evaporation enthalpies of hydrogen, carbon monoxide and methane as examples.
Stronger contributions are provided by hydrogen bonds with 20-40 kJ/mol bond (depending on polarisation). See as examples the enthalpies of melting and evaporation of water, methanol and formic acid and also enthalpies of hydration. Hydrogen bonds are also responsible for the fact that the boiling point of water is 100 °C, while that of hydrogen sulphide is only -83 °C (see boiling point anomaly).
Very strong contributions are made by ion-ion interactions in crystals. In the crystal, sodium chloride does not consist of discrete NaCl molecules, but of an equal number of sodium cations and chloride anions arranged exactly in the crystal lattice according to Coulomb forces.

Enthalpy in chemistry (thermochemistry)

In a narrower sense, thermochemistry describes only the intramolecular forces, i.e. the energetic relationships between the individual atoms of a molecule. Covalent bonds contain approx. 150-1000 kJ/mol of binding energy, ionic bonds approx. five times this amount.

If the standard enthalpies of formation of reactants and products are known, a possible chemical reaction can be roughly balanced energetically. The most important question is often whether a process is endothermic or exothermic and to what extent.

$\Delta H_{\mathrm {Reaktion} }^{0}=\sum \Delta H_{f,\mathrm {Produkte} }^{0}-\sum \Delta H_{f,\mathrm {Edukte} }^{0}$

Details such as evaporation, melting, solvation or crystallisation enthalpies can be used to specify partial steps within the chemical reaction in terms of energy. The energy content of the reaction can be specified.

Reaction enthalpy

→ Main article: Enthalpy of reaction

The enthalpy of reaction is the energy released or required when new chemical bonds are formed between the molecules of two substances. It depends on the reaction partners (reactants) and the type of chemical bond in the product. To calculate it, one compares the sum of the enthalpies of formation of the products with that of the reactants. The difference is the enthalpy of reaction, which can then be standardised by reference to the amount of substance in the product of interest:

2 Na (s)	+	Cl2 (g)	$\longrightarrow$	2 NaCl (s)
2 × 0 kJ/mol		0 kJ/mol		2 × -411 kJ/mol	Formation enthalpies (25 Â°C)
$\Rightarrow$ Reaction enthalpy = 2 mol × (-411) kJ/mol - 2 mol × 0 kJ/mol - 1 mol × 0 kJ/mol = -822 kJ.

The reaction is therefore exothermic. Dividing by the amount of substance obtained, in this case 2 mol sodium chloride, yields its molar enthalpy of formation of -411 kJ/mol NaCl (25 °C) (in this example, however, already assumed at the beginning).

Standard enthalpy of combustion

Combustion is also a chemical reaction. The enthalpy of reaction of the combustion reaction or the standard enthalpy of combustion of a substance is the enthalpy change that occurs when a substance burns completely under excess O2 (O2 overpressure) and standard conditions (101.325 kPa and 25 °C). By definition, this heat of combustion refers to the formation of gaseous carbon dioxide and liquid water (or N2) as end products; no gaseous water can form under excess oxygen pressure. It is designated ΔVH0 or ΔcH0 (c for combustion) and its absolute amount is identical to the calorific value Hs.

The following reaction is carried out in an autoclave tube with excess oxygen pressure:

_C3H8 (g)	+	5 O2 (g)	$\longrightarrow$	3 _CO2 (g)	+	4 H2O (l)
-103.2 kJ/mol		5 × 0 kJ/mol		3 × -393.5 kJ/mol		4 × -285.8 kJ/mol

$\Rightarrow$ reaction enthalpy = 3 mol × (-393.5) kJ/mol + 4 mol × (-285.8) kJ/mol - 1 mol × (-103.2) kJ/mol - 5 mol × (0) kJ/mol = -2.22 MJ.

Division by the amount of substance used, in this case 1 mol propane, gives its molar enthalpy of combustion of -2.22 MJ/mol propane (25 °C)

The same reaction in an open burner flame; only gaseous combustion products are formed:

_C3H8 (g)	+	5 O2 (g)	$\longrightarrow$	3 _CO2 (g)	+	4 H2O (g)
-103.2 kJ/mol		5 × 0 kJ/mol		3 × -393.5 kJ/mol		4 × -241.8 kJ/mol

$\Rightarrow$ reaction enthalpy = 3 mol × (-393.5) kJ/mol + 4 mol × (-241.8) kJ/mol - 1 mol × (-103.2) kJ/mol - 5 mol × (0) kJ/mol = -2.04 MJ.

Division by the amount of substance used, in this case 1 mol propane, gives its molar enthalpy of combustion of -2.04 MJ/mol propane (25 °C)

Advanced application

It is tedious to look up the standard enthalpies of formation of the reactants and products for each reaction, and in the correct state of aggregation. Moreover, with larger molecules one quickly encounters a "data vacuum". The following simplified considerations have proven themselves in practice:

It is irrelevant whether one brominates a long-chain alkyl-substituted ethylene or ethylene itself, the heat of reaction per (C=C) double bond is largely the same.
It is irrelevant whether one calculates a reaction completely in the liquid phase or completely in the gas phase, the heat of reaction hardly influences this.
It is insignificant (some deviations) to calculate reactions carried out at 150 °C for 25 °C standard conditions. (The enthalpy of reaction can be calculated for any temperature if the temperature dependence of the molar heats of all reactants is known).

Therefore, one can calculate normal organic chemical conversions such as halogen additions, cycloadditions, esterifications with acids or anhydrides, hydrolyses etc. with the help of numerous tabulated increments for gaseous molecules according to Benson.

In the following example, the reaction energy of the bromine addition to ethylene is calculated with Benson increments and estimated for comparison from binding energies of involved bonds. (Note: Bonding energies are averaged dissociation energies, not standard enthalpies of formation!)

Bromine addition to an alkene, reaction enthalpy calculated with standard enthalpies of formation:

H2C=CH2	+	Br2	$\longrightarrow$	H2BrC-CBrH2
52 kJ/mol		0 kJ/mol		-39 kJ/mol

$\Rightarrow$ Reaction enthalpy (25 °C, all values for gaseous state) = (-39 - 52) kJ/mol = -91 kJ/mol Double bond

Bromine addition to an alkene, reaction enthalpy calculated with increments according to Benson:

H2C=CH2	+	Br2	$\longrightarrow$	H2BrC-CBrH2
2 Cd-(H)₂: 2× +28.1 kJ/mol				2 C-(H)₂(Br)(C): 2× -22.6 kJ/mol

$\Rightarrow$ Reaction enthalpy (calculated according to Benson) = ( -45.2 - (+56.2)) kJ/mol = -101 kJ/mol Double bond

Bromine addition to an alkene, reaction enthalpy estimated with binding energies:

H2C=CH2	+	Br2	H2BrC-CBrH2
4 C-H: 4×>455 kJ/mol			4 C-H: 4× 380±50 kJ/mol
1 C=C: 1× 614 kJ/mol			1 C-C: 1× 348 kJ/mol
1 Br-Br: 193 kJ/mol			2 C-Br: 2× 260±30 kJ/mol

$\Rightarrow$ Reaction enthalpy (estimated from bond energies) = ( 2388±200 - 2627) kJ/mol = -239±200 kJ/mol Double bond

The best estimation for reaction enthalpies is achieved with standard enthalpies of formation or increments according to Benson; when using "binding energies", the uncertainty of ±200 kJ/mol is much too high.

Technical applicability

The reaction enthalpies of organic reactions are in the range -160 to +100 kJ per mole of "reactive centres". All addition reactions with epoxides, anhydrides and halogens prove to be very strongly exothermic. These thermochemical observations make no statement about how quickly these reaction heats are released. They only make the statement that this heat is released by the end of the reaction. Each reaction increases its speed by a factor of two to three with a temperature increase of 10 K. Conversely, a twofold dilution of the reactants often means a halving of the reaction rate or heat output of the reaction. Calculated reaction enthalpies are used to calculate the temperature curve in a system of reactants and solvents via their heat capacities. Large-scale plants only have limited cooling capacities (-heat/time), this is often not taken into account in laboratory experiments.

Binding energy / dissociation energy

→ Main article: Binding energy (chemistry)

The binding energy or binding strength indicates the "stability" of the covalent bond. The determination is only possible directly for diatomically symmetrical molecules such as hydrogen or halogens. In these cases, the dissociation energy to form two identical radicals can be easily measured/calculated. For "element radicals", the standard enthalpy of formation of radicals is also called atomisation enthalpies.

In all other cases, values for the "binding energy" are only possible indirectly by comparing several dissociation energy measurements on homologous molecules. The values vary depending on the substitution pattern at the radical centres.

The standard enthalpy of formation of gaseous

Bromine radicals includes the enthalpy of vaporisation (31 kJ/mol) necessary to convert liquid bromine into gaseous bromine.
Iodine radicals includes the sublimation enthalpy (62 kJ/mol) necessary to convert crystalline iodine into gaseous iodine.
carbon radicals is identical to the standard enthalpy of formation of gaseous carbon vapour.

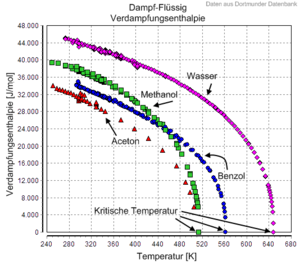
Temperature dependence of the enthalpy of vaporisation of water, methanol, benzene and acetone.

Thermodynamic properties of enthalpy

Enthalpy as a fundamental function

Consider a system whose properties are defined by the state variables entropy , volume and mole numbers $N_{1}...N_{r}$ the chemical components, then the internal energy the system is expressed as a function of the mentioned state variables (namely all extensive variables of the system),

$U=U(S,V,N_{1},...,N_{r})$

a fundamental function of the system. It describes the system completely; all thermodynamic properties of the system can be derived from it.

Often, however, these variables are inconvenient for practical work and one would prefer to have, for example, the temperature or the pressure in the variable list. In contrast to the usual procedure, a change of variable in the present case must not be done by a simple substitution, as otherwise information is lost. If, for example, the volume is to be replaced by the pressure could be $p(S,V,N_{i})$ eliminated from the functions $U(S,V,N_{i})$ and obtain a function of the form $U(S,p,N_{i})$ However, since the pressure is thermodynamically defined as the partial derivative of the internal energy with respect to the volume

$p=-\left({\frac {\partial U}{\partial V}}\right)_{S,N_{1},...,N_{r}}$

this formulation would be equivalent to a partial differential equation for which would define only up to indefinite functions. This would still be a description of the system under consideration, but it would not be a complete description and thus no longer a fundamental function.

To change variables while preserving the complete information, a Legendre transformation must be performed. For example, if the variable list $(S,p,N_{1},...,N_{r})$ the transformation is as follows:

$H(S,p,N_{1},...,N_{r}):=U(S,V,N_{1},...,N_{r})-\left({\frac {\partial U}{\partial V}}\right)_{S,N_{1},...,N_{r}}\cdot V=U+p\ V$ .

The Legendre transform $H=U+p\ V$ is called enthalpy. It is again a fundamental function if it is given as a function of the variables $(S,p,N_{1},...,N_{r})$ - these are the natural variables of enthalpy. It can also be expressed as a function of other variables, but then it is no longer a fundamental function.

The origin of the enthalpy from a Legendre transformation explains the additive term $p\,V$ It compensates for the loss of information that would otherwise be associated with the change of variable.

Fundamental functions that have the dimension energy are also called thermodynamic potentials. Enthalpy is therefore a thermodynamic potential.

Derivatives of enthalpy

If one starts from the internal energy as a function of its natural variables and forms its total differential, one obtains:

$\mathrm {d} U(S,V,N_{1},...,N_{r})=\left({\frac {\partial U}{\partial S}}\right)_{V,N_{1},...,N_{r}}\mathrm {d} S+\left({\frac {\partial U}{\partial V}}\right)_{S,N_{1},...,N_{r}}\mathrm {d} V\,+\,\sum _{i=1}^{r}\left({\frac {\partial U}{\partial N_{i}}}\right)_{S,V,N_{j\neq i}}\mathrm {d} N_{i}$ .

The partial derivatives occurring here are interpreted in thermodynamics as the definitions of temperature , pressure and chemical potential of the ith substance μ $\mu _{i}$ :

${\begin{aligned}T&:=\left({\frac {\partial U(S,V,N_{1},...,N_{r})}{\partial S}}\right)_{V,N_{1},...,N_{r}},\\p&:=-\left({\frac {\partial U(S,V,N_{1},...,N_{r})}{\partial V}}\right)_{S,N_{1},...,N_{r}},\\\mu _{i}&:=\left({\frac {\partial U(S,V,N_{1},...,N_{r})}{\partial N_{i}}}\right)_{S,V,N_{j\neq i}},\end{aligned}}$

so that the differential can also be written as

$\mathrm {d} U(S,V,N_{1},...,N_{r})=T\,\mathrm {d} S-p\,\mathrm {d} V\,+\,\sum _{i=1}^{r}\mu _{i}\,\mathrm {d} N_{i}$ .

The total differential of enthalpy as a function of its natural variables is on the one hand formally

$\mathrm {d} H(S,p,N_{1},...,N_{r})=\left({\frac {\partial H}{\partial S}}\right)_{p,N_{1},...,N_{r}}\mathrm {d} S+\left({\frac {\partial H}{\partial p}}\right)_{S,N_{1},...,N_{r}}\mathrm {d} p\,+\,\sum _{i=1}^{r}\left({\frac {\partial H}{\partial N_{i}}}\right)_{S,p,N_{j\neq i}}\mathrm {d} N_{i}\quad (*)$ .

and on the other hand, using their definition

${\begin{aligned}\mathrm {d} H&=\mathrm {d} (U+pV)\\&=\mathrm {d} U+\mathrm {d} (pV)\\&=T\,\mathrm {d} S-p\,\mathrm {d} V+\,\sum \mu _{i}\,\mathrm {d} N_{i}\,+\mathrm {d} (pV)\\&=T\,\mathrm {d} S-p\,\mathrm {d} V+\,\sum \mu _{i}\,\mathrm {d} N_{i}\,+p\,\mathrm {d} V+V\mathrm {d} p\\&=T\,\mathrm {d} S+V\mathrm {d} p\,+\,\sum \mu _{i}\,\mathrm {d} N_{i}\quad (*)\end{aligned}}$

so that from the comparison of the coefficients in the marked equations follows

$\left({\frac {\partial H}{\partial S}}\right)_{p,N_{1},...,N_{r}}=T$ ,

and

$\left({\frac {\partial H}{\partial p}}\right)_{S,N_{1},...,N_{r}..}=V$

and

$\left({\frac {\partial H}{\partial N_{i}}}\right)_{S,p,N_{j\neq i}}=\mu _{i}$ .

The derivation simultaneously shows how the addition of the term $p\,V$ list of independent variables from $(S,V,...)$ to $(S,p,...)$ removing the term dependent on $\mathrm {d} V$ the total differential and adding a ${\mathrm {d}}p$ term dependent on

The second of the marked equations is a "differential fundamental function", namely the differential enthalpy as a function of its natural variables:

$\mathrm {d} H(S,p,N_{1},...,N_{r})=T\,\mathrm {d} S+V\mathrm {d} p\,+\,\sum _{i=1}^{r}\mu _{i}\,\mathrm {d} N_{i}$ .

Minimum enthalpy principle

According to the Second Law of Thermodynamics, a closed system takes as its equilibrium state among the attainable states the one that has the highest entropy at the given internal energy. From this maximum principle of entropy, a minimum principle of internal energy can be derived: If entropy is kept constant, a system adopts as its equilibrium state that state which has the lowest internal energy.

A similar minimum principle exists for enthalpy: A system that is kept at constant pressure assumes as its equilibrium state, of all the states that can be reached with this pressure, the one in which the enthalpy has the smallest possible value.

To prove this, consider a system whose pressure is kept at a constant value. Pressure control can be achieved, for example, by the system under consideration being in contact, via a movable adiabatic wall, with a second system that invariably has the desired pressure (in thermodynamic terms: a pressure reservoir). By moving the contact wall, the system under consideration can, if necessary, "exchange volume" with the pressure reservoir until it has brought its pressure back into line with that of the reservoir. The total system formed by the system under consideration and the pressure reservoir assumes the lowest possible internal energy $U_{\mathrm {Ges} }$ , and at the energy minimum applies:

$\mathrm {d} U_{\mathrm {Ges} }=\mathrm {d} U+\mathrm {d} U_{\mathrm {Res} }=0$ .

Since only volume is exchanged with the reservoir according to its definition, the internal energy of the reservoir can only be changed by performing volume change work on it: $\mathrm {d} U_{\mathrm {Res} }=-p_{\mathrm {Res} }\,\mathrm {d} V_{\mathrm {Res} }$ , and thus

$\mathrm {d} U-p_{\mathrm {Res} }\,\mathrm {d} V_{\mathrm {Res} }=0$ .

When the partition is displaced, $\mathrm {d} V_{\mathrm {Res} }=-\mathrm {d} V$ such that

$\mathrm {d} U+p_{\mathrm {Res} }\,\mathrm {d} V=0$ .

Since the pressure of the reservoir, $p_{\mathrm {Res} }$ , is constant according to the prerequisite, it can be written

$\mathrm {d} (U+p_{\mathrm {Res} }\,V)=0$ .

The extremal properties of the function $U+p_{\mathrm {Res} }\,V$ investigated in more detail. However, since one expects pressure equilibrium between the system under consideration (pressure ) and the pressure reservoir (pressure $p_{\mathrm {Res} }$ ), it is obvious to limit the further investigation to the states with the property $p=p_{\mathrm {Res} }$ . However, on the subset of these states $U+p_{\mathrm {Res} }\,V$ identical to $U+p\,V$ . It therefore holds

$\mathrm {d} H=\mathrm {d} (U+p\,V)=0$ , provided that $p=p_{\mathrm {Res} }$ .

As can be shown, the second derivative of is positive in this condition, so that the extremum of enthalpy found is indeed a minimum.

The minimum principle for the internal energy of the total system at constant entropy thus leads to the enthalpy of the system under consideration assuming a minimum on the subset of states with constant pressure $p=p_{\mathrm {Res} }$ assumes a minimum. If the system is not yet in equilibrium, it moves voluntarily (under isobaric conditions) to states of lower enthalpy. Equilibrium is reached with the state in which the enthalpy has the smallest possible value under the given conditions.

If one wants to determine the state of equilibrium with the help of the (generally and always valid) entropy criterion, the maximum of the total entropy must be determined, i.e. the sum of the entropies of the system under investigation and its environment. Therefore, not only the change of the system entropy during a change of state must be considered, but also the entropy change that the system produces there through reaction on the environment. The enthalpy criterion is a reformulation of the entropy criterion, in which only properties of the system under consideration are taken into account and which automatically takes into account the retroactive effect on the environment (under isobaric conditions). When using the enthalpy criterion, the determination of the (isobaric) state of equilibrium can thus be limited to the observation of the system, which noticeably facilitates the investigations.

If the enthalpy is $(S,p,N_{i})$ expressed as a function of its natural variables , the constant pressure condition reduces the list of variables by and the enthalpy depends only on the variables $(S,N_{i})$ This simplification demonstrates one of the possible advantages of using enthalpy in appropriate cases. The equilibrium state could also be determined by finding the minimum of the internal energy of the system under consideration, $U(S,V,N_{i})$ but the condition of constant pressure would in this case not lead to a simplification of the function but to complicated dependencies between the variables $(S,V,N_{i})$ . Additional problems would arise if the equation of state $p=p(S,V,N_{i})$ is not explicitly known.

For a real physical or chemical process, the atmosphere can often serve as a pressure reservoir. Because of its large volume, its pressure does not change appreciably when a system performs volume change work on it. The conditions for the applicability of the minimum enthalpy principle are thus fulfilled if a system is adiabatically isolated from the environment (to prevent heat exchange with the environment and thus keep entropy constant) and coupled to the ambient atmospheric pressure via a movable piston or similar device (to keep the system pressure constant).

In laboratory practice, however, such adiabatic systems rarely occur. Chemical reactions usually do not take place in adiabatically insulated vessels, so that heat can be exchanged with the environment. The atmosphere then serves not only as a pressure reservoir but also as a heat reservoir: it keeps pressure and temperature constant. The thermodynamic potential that assumes a minimum under these conditions is the Gibbs energy $G=U+p\,V-T\,S$ .

Enthalpy and heat capacity

→ Main article: Specific heat capacity

If one adds the specific (i.e. related to the mass) amount of heat $\mathrm {d} q$ a system and thereby causes a temperature change $\mathrm {d} T$ then the specific heat capacity the system is defined by the equation

$\mathrm {d} q=c\cdot \mathrm {d} T$

$c={\frac {\mathrm {d} q}{\mathrm {d} T}}$ .

The specific heat capacity depends not only on the material but also on the process control. If the heat supply is isochoric (i.e. at constant volume), then the total amount of heat supplied contributes to the increase of the specific internal energy $\mathrm {d} u$

$\mathrm {d} q=\mathrm {d} u$

and the process is described by the specific heat capacity at constant volume, $c_{v}$

$c_{v}=\left({\frac {\partial u}{\partial T}}\right)_{v}$ ,

which is therefore the derivative of the specific internal energy according to the temperature at constant volume.

If the heat input is isobaric, then the specific heat input is equal to the increase in specific enthalpy ${\mathrm {d}}h$ :

$\mathrm {d} q=\mathrm {d} h$

and the process is described by the specific heat capacity at constant pressure, $c_{p}$

$c_{p}=\left({\frac {\partial h}{\partial T}}\right)_{p}$ ,

which is therefore the derivative of the specific enthalpy according to the temperature at constant pressure.

Since to achieve a desired temperature increase in the isobaric case, the volume change work to be performed by the system must be additionally supplied, it is to be expected that the isobaric specific heat capacity of a substance will be greater than the isochoric one. A closer look must take into account that the expansion of the system usually also changes its internal energy. However, it can be shown that generally applies:

$c_{p}-c_{v}\,=\,\left({\frac {\alpha ^{2}}{\kappa }}\right)Tv$ .

On the right side, the temperature , the specific volume , the square of the isobaric thermal expansion coefficient α $\alpha$ and (for thermodynamic stability reasons) the isothermal compressibility κ $\kappa$ become negative, so that always

$c_{p}\geq c_{v}$

is. In some cases, $c_{p}$ may be 30% greater than $c_{v}$ .

Temperature and pressure dependence of enthalpy

Tabulations of enthalpy usually refer to a specific temperature and pressure for reasons of space. If the enthalpy is to be determined for other conditions, formulas are desirable that allow the transition from the reference state to other temperatures and pressures. It is advantageous if only the knowledge of directly measurable quantities is required for the conversion.

For a closed system that is in equilibrium and in which no chemical reactions take place ( $\mathrm {d} N_{i}=0$ ), an infinitesimal change in enthalpy is given, as explained above, by

$\mathrm {d} H=T\ \mathrm {d} S+V\ \mathrm {d} P$ .

The differential $\mathrm{d}S$ can be developed - understood as a function of the variables of interest here and - as follows:

${\begin{aligned}\mathrm {d} H&=T\left\{\left({\frac {\partial S}{\partial T}}\right)_{p}\mathrm {d} T+\left({\frac {\partial S}{\partial p}}\right)_{T}\mathrm {d} p\right\}+V\mathrm {d} p\\&=T\left({\frac {\partial S}{\partial T}}\right)_{p}\mathrm {d} T+\left\{V+T\left({\frac {\partial S}{\partial p}}\right)_{T}\right\}\mathrm {d} p\end{aligned}}$

With the help of the identities

$T\left({\frac {\partial S}{\partial T}}\right)_{p}=\left({\frac {\partial Q}{\partial T}}\right)_{p}=\left({\frac {\partial H}{\partial T}}\right)_{p}$ (because according to the $\mathrm {d} Q=T\ \mathrm {d} S$ Second Law).

and

$\left({\frac {\partial S}{\partial p}}\right)_{T}=-\left({\frac {\partial V}{\partial T}}\right)_{p}$ (one of the Maxwell relations)

follows

$\mathrm {d} H=\left({\frac {\partial H}{\partial T}}\right)_{p}\mathrm {d} T+\left\{V-T\left({\frac {\partial V}{\partial T}}\right)_{p}\right\}\mathrm {d} p$ ,

which can be calculated using the isobaric heat capacity $C_{p}=\left({\frac {\partial H}{\partial T}}\right)_{p}$ and the isobaric thermal expansion coefficient α $\alpha ={\frac {1}{V}}\left({\frac {\partial V}{\partial T}}\right)_{p}$ exclusively by the measurable quantities , $C_{p}$ and α \alpha $\alpha$

$\mathrm {d} H=C_{p}\ \mathrm {d} T+V(1-\alpha \ T)\ \mathrm {d} p$ .

For a finitely large change of state from the state $(T_{1},p_{1})$ to the state $(T_{2},p_{2})$ integrate over this infinitesimal change of state:

$H_{2}-H_{1}=\int _{T_{1}}^{T_{2}}C_{p}\ \mathrm {d} T+\int _{p_{1}}^{p_{2}}V(1-\alpha \ T)\ \mathrm {d} p$ .

If the change of state is associated with a phase transition, the relevant latent heat must also be taken into account.

The quantities , $C_{p}$ and α $\alpha$ are usually themselves dependent on temperature and pressure. These dependencies must be known so that the integrals can be carried out.

Since enthalpy is a state variable, the integrals do not depend on the choice of path along which to integrate. A convenient choice of path is to first perform the temperature integral on a constant pressure path $(T_{2},p_{1})$ connecting the initial state $(T_{1},p_{1})$ with an intermediate state For this, $C_{p}$ in the temperature range from $T_{1}$ to $T_{2}$ at the fixed pressure must be $p_{1}$ known. Then the pressure integral is performed on the constant temperature path $(T_{2},p_{2})$ connecting $(T_{2},p_{1})$ to For this, must be $T_{2}$ known in $V\alpha$ the pressure range from $p_{1}$ to $p_{2}$ at the fixed temperature

Alternatively, the integration can first be carried out on a constant temperature path from $(T_{1},p_{1})$ to $(T_{1},p_{2})$ which $V\alpha$ in the pressure range from $p_{1}$ to $p_{2}$ at the fixed temperature $T_{1}$ must be known. Subsequently, the path at constant pressure leads from $(T_{1},p_{2})$ to for $(T_{2},p_{2})$ which $C_{p}$ in the temperature range from $T_{1}$ to $T_{2}$ at the fixed pressure must be known. $p_{2}$

If the process is isobaric, $p_{1}=p_{2}$ the pressure integral is omitted and only the knowledge of the temperature-dependent heat capacity $C_{p}$ at the fixed pressure in question is necessary:

$H_{2}-H_{1}=\int _{T_{1}}^{T_{2}}C_{p}\ \mathrm {d} T\quad \mathrm {(isobar)}$ .

Questions and Answers

Q: What is enthalpy?

A: Enthalpy is a concept used in science and engineering to calculate heat and work in a substance.

Q: Where does the name "enthalpy" come from?

A: The name "enthalpy" comes from the Greek word "enthalpos" (ενθαλπος), which means "to put heat into".

Q: Who made up the idea and word "enthalpy"?

A: The Dutch scientist Heike Kamerlingh Onnes made up the idea and word "enthalpy" in 1909.

Q: How does enthalpy relate to energy?

A: Enthalpy accounts for the energy used or released when a substance grows or shrinks, but it is not the same as energy.

Q: Why do scientists often calculate the change in enthalpy rather than the change in energy?

A: Scientists often calculate the change in enthalpy because it takes into account the energy used or released when a substance changes size.

Q: What happens when heat energy enters a system containing a fixed amount of gas?

A: When heat energy enters a system containing a fixed amount of gas, it can either increase the internal energy of the gas or lead to some work being done to expand the system.

Q: How does enthalpy take into account the factors of pressure and volume?

A: Enthalpy takes into account the factors of pressure and volume by considering the work done, which is the product of pressures and volume.