Elliptic curve

This article deals with elliptical curves. For the ellipse as a geometric figure see Ellipse.

In mathematics, elliptic curves are special algebraic curves on which an addition is geometrically defined. This addition is used in cryptography to construct secure encryption methods. However, elliptic curves also play an important role in pure mathematics. Historically, they arose through the parametrisation of elliptic integrals as their inverse functions (elliptic functions).

An elliptic curve is a smooth algebraic curve of order 3 in the projective plane. Elliptic curves are usually represented as curves in the affine plane, but they also have an additional point at infinity.

Elliptic curves over the body of real numbers can be regarded as the set of all (affine) points $(x,y)\in {\mathbb {R}}^{2}$ which satisfy the equation

$y^{2}=x^{3}+ax+b$

together with a so-called point at infinity (written as $\infty$ or ${\mathcal O}$ ). The (real) coefficients and must satisfy the condition that for the discriminant of the cubic polynomial in on the right-hand side $4a^{3}+27b^{2}\neq 0$ holds, to exclude singularities (the roots of the polynomial are then different in pairs, the curve has no colons or other singularities).

In general, however, one will not limit oneself to the case of real coefficients and solutions when considering the given equation, but rather consider the case where coefficients and solutions originate from the body of complex numbers. Elliptic curves over the body of rational numbers, over finite bodies and over p-adic bodies were also studied in detail. The theory of elliptic curves therefore connects very different subfields of mathematics. The investigation of elliptic curves over the rational numbers or finite bodies is the subject of number theory and a special case of the abelian varieties also considered in higher dimensions. Their investigation over the complex numbers is a classical field of function theory.

Every elliptic curve over the complex numbers can be represented as a complex torus with the help of a lattice in the complex number plane, which already results from the double periodicity of elliptic functions (see Weierstrass elliptic function). Their Riemann surface is topologically a torus and, via the associated division of the complex plane by a lattice, an abelian group. This group structure also carries over to elliptic curves over the rational numbers and to a special kind of addition for points on elliptic curves (see below). In 1994, the mathematician Andrew Wiles proved the modularity theorem, which states that all elliptic curves over the rational numbers are parameterised by modular forms. With the help of this theorem, it was possible to prove Fermat's Great Theorem, a well-known number-theoretical statement that is easy to formulate but difficult to prove.

Practical applications of elliptic curves are found in modern encryption methods (elliptic curve cryptosystem), which use the above-mentioned special addition of points on elliptic curves for the definition of one-way functions. Further applications can be found in the factorisation of natural numbers.

If instead of cubic polynomials those of higher than fourth degree are considered, one obtains hyperelliptic curves (which have higher topological gender).

Elliptic curve $5y^{2}=x^{3}-3x+5$ over the body of real numbers

Solutions of the equation $y^{2}=x^{3}+ax+b$ for different values of (a,b) . In the case $(a,b)=(0,0)$ the curve is singular and therefore not an elliptic curve.

History

The theory of elliptic curves first developed in the context of function theory. Elliptic integrals occur in various geometric or physical problems - for example, in determining the arc length of ellipses. Inverse functions could be determined for these integral functions. These meromorphic functions were called elliptic functions because of this context (for their history see there). As will be shown below, by means of elliptic functions one can uniquely assign a torus to any elliptic curve over the body of complex numbers $\mathbb {C}$ assigned to a torus. In this way the elliptic curves can then be classified and because of this connection they have received their name.

Since the end of the 19th century, arithmetic and number-theoretic questions have been at the centre of theory. It could be shown that elliptic curves can be meaningfully defined on general bodies and it was shown - as described before - that an elliptic curve can be interpreted as a commutative group (which goes back to Henri Poincaré).

In the 1990s, Andrew Wiles, following preliminary work by Gerhard Frey and others, was able to prove Fermat's 17th century conjecture by means of the theory of elliptic curves.

Affine and projective plane

The two-dimensional space of the -rational projective points is defined as

$\mathbb {P} ^{2}(K)=\{(X,Y,Z)|X,Y,Z\in K{\text{ nicht alle gleich 0}}\}/\!{\sim }$

with the equivalence relation

$(X_{1},Y_{1},Z_{1})\sim (X_{2},Y_{2},Z_{2})\Leftrightarrow \exists \lambda \in K^{\ast }:(X_{1},Y_{1},Z_{1})=(\lambda X_{2},\lambda Y_{2},\lambda Z_{2})$ .

Points from $\mathbb{P}^2(K)$ are usually (X:Y:Z) notated as distinguish them from points in three-dimensional affine space.

The projective plane $\mathbb{P}^2(K)$ can be represented as the union of the set

$\{(X:Y:1)|X,Y\in K\}$

with the hyperplane of Z=0 generated by ${\mathbb P}^{2}(K)$ :

$H=\{(X:Y:0)|X,Y\in K{\text{ nicht beide gleich 0}}\}$

To represent projective cubes in the affine plane, one then identifies for $Z\neq 0$ the projective point $(X:Y:Z)=\left({\frac {X}{Z}}:{\frac {Y}{Z}}:1\right)=(x:y:1)$ with the affine point (x,y) .

In the case of an elliptic curve, the (projective) polynomial equation has exactly one solution with Z=0 namely the point at infinity ${\mathcal O}=(0:1:0)$ .

Definition

is called an elliptic curve over the body if one of the following (pairwise equivalent) conditions is fulfilled:

is a smooth projective curve over of gender 1 with a point ${\mathcal O}$ whose coordinates lie in
is a smooth projective cubic over with a point ${\mathcal O}$ whose coordinates lie in
is a smooth equation given by a Weierstrass equation

$Y^{2}Z+a_{1}XYZ+a_{3}YZ^{2}=X^{3}+a_{2}X^{2}Z+a_{4}XZ^{2}+a_{6}Z^{3}$

given projective curve with coefficients $a_i \in K$ . If one writes

$F(X,Y,Z)=Y^{2}Z+a_{1}XYZ+a_{3}YZ^{2}-X^{3}-a_{2}X^{2}Z-a_{4}XZ^{2}-a_{6}Z^{3},$

then is just the zero set of the homogeneous polynomial $F\in K[X,Y,Z]$ . (Note: The point $(0:1:0)={\mathcal {O}}$ satisfies the polynomial equation in any case, so lies on .)

If one takes as an affine curve, one obtains an affine Weierstrass equation

$y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}$

(in long Weierstrass form / Weierstrass normal form) resp. an affine polynomial $f(x,y)=y^{2}+a_{1}xy+a_{3}y-x^{3}-a_{2}x^{2}-a_{4}x-a_{6}\in K[x,y]$ . In this case, is just the set of (affine) points satisfying the equation, together with the so-called "infinitely distant point" ${\mathcal O}$ , also $\infty$ written as

Isomorphic elliptic curves

Definition

Every elliptic curve is $f(x,y)\in K[x,y]$ described by a projective polynomial $F(X,Y,Z)\in K[X,Y,Z]$ or by an affine polynomial Two elliptic curves $E_{1}$ and are called $E_{2}$ isomorphic if the Weierstrass equation of is $E_{2}$ derived from that of $E_{1}$ by a coordinate change of the form

$x\mapsto u^{2}x+r$

$y\mapsto u^{3}y+su^{2}x+t$

with $u,r,s,t\in {\bar {K}},u\neq 0$ arises. The most important properties of elliptic curves do not change when such a change of coordinates is carried out.

Short Weierstrass equation

If an elliptic curve over a body with characteristic $\operatorname {char}(K)\not \in \{2,3\}$ is given by the Weierstrass equation

$y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}$

then there exists a change of coordinates which transforms this Weierstrass equation into the equation

$y^{2}=x^{3}+ax+b$

transformed. This is called a short Weierstrass equation. The elliptic curve defined by this short Weierstrass equation is isomorphic to the original curve. It is therefore often assumed without qualification that an elliptic curve is given from the outset by a short Weierstrass equation.

A further result of the theory of Weierstrass equations is that an equation of the (short Weierstrass) form

$y^{2}=x^{3}+ax+b$

describes a smooth curve exactly when the discriminant Δ $\Delta _{E}$ of the polynomial $x^{3}+ax+b$ ,

$\Delta _{E}=-4a^{3}-27b^{2},$

does not disappear. The discriminant is proportional to the product ${(\lambda _{1}-\lambda _{2})}^{2}\cdot {(\lambda _{1}-\lambda _{3})}^{2}\cdot {(\lambda _{2}-\lambda _{3})}^{2}$ with the roots λ $\lambda _{i}$ of the cubic polynomial and does not vanish, if the roots are pairwise different.

Examples

$E_{1}\colon y^{2}=x^{3}-x+1$ and $E_{2}\colon y^{2}=x^{3}+2x-{\sqrt {3}}$ are elliptic curves over $\mathbb {R}$ , since Δ $\Delta _{E_{1}}=4-27=-23\neq 0$ and Δ $\Delta _{E_{2}}=-32-81=-113\neq 0$ .
$E\colon y^{2}=x^{3}-x$ is an elliptic curve over both $\mathbb {Q}$ and over $\mathbb {R}$ since the discriminant Δ $\Delta _{E}=4\neq 0$ . Over a body with characteristic on the other hand, Δ $\Delta _{E}=0$ and singular, i.e. not an elliptic curve.
$E\colon y^{2}=x^{3}+1$ is an elliptic curve over any body with characteristic not equal to since Δ $\Delta _{E}=-27=-3^{3}\neq 0$

Above the real numbers, the discriminant gives information about the shape of the curve in the affine plane. For Δ $\Delta _{E}>0$ the graph of the elliptic curve {\displaystyle two components (left figure), for Δ E < $\Delta _{E}<0$ one component (right figure).

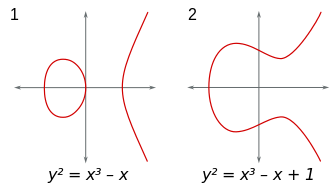
Diagram of exemplary curves

Group operation

Elliptic curves have the special feature that they are commutative groups with regard to the point-wise addition described in this section. In the first subsection, this addition is illustrated geometrically before it is further formalised in the following sections.

Geometric interpretation

Geometrically, the addition of two points of an elliptic curve can be described as follows: The point at infinity is the neutral element $\infty$ . The reflection of a rational point on the -axis yields again a rational point of the curve, the inverse of . The straight line through the rational points P,Q intersects the curve at a third point, mirroring this point on the -axis yields the rational point P+Q .

In the case of a tangent to the point (i.e. the limiting case $Q\to P$ on the curve) this construction (intersection of the tangent with the curve, then mirroring) yields the point P+P . If no corresponding intersection points can be found, the point at infinity is used, and in the case of the tangent without a second intersection point, for example, we have: $P+P=\infty$ . Often the neutral point is also called ${\mathcal O}$ The point P+P denoted by , correspondingly one defines $kP=P+\dotsb +P$ as -fold addition of the point .

One can show that this "addition" is both commutative and associative, so that it actually satisfies the laws of an abelian group. The Cayley-Bacharach theorem can be used to prove the associative law.

Let be a rational point of the elliptic curve. If not the point ${\mathcal O}$ then every rational point of the curve can be reached in this way (i.e., for every point on the curve there exists a natural number with $Q=kP$ ), if one knows the correct generators of the group.

The task of finding P,Q this value from given points called the elliptic curve discrete logarithm problem (ECDLP for short). It is assumed that the ECDLP (with a suitable choice of curves) is difficult, i.e. cannot be solved efficiently. This makes elliptic curves suitable for realising asymmetric cryptosystems on them (such as a Diffie-Hellman key exchange or an Elgamal cryptosystem).

Addition of two different points

$P=(x_{P},y_{P})$ and be $Q=(x_{Q},y_{Q})$ the components of the points and . $R:=P+Q:=(x_{R},y_{R})$ denotes the result of the addition This point thus has the components $(x_{R},y_{R})$ . Furthermore set

$s:={\frac {y_{P}-y_{Q}}{x_{P}-x_{Q}}}$ .

Then the addition is given by $P+Q=(x_{R},y_{R})$

$x_{R}:=s^{2}-x_{P}-x_{Q}$ and
$y_{R}:=-y_{P}+s(x_{P}-x_{R})$

defined.

The two points and must not have the same coordinate, otherwise it is not possible to calculate the slope since then either P=Q or P=-Q applies. Adding $P+(-P)$ gives $s={\tfrac {2y_{P}}{0}}$ , which defines the result as $\infty$ (neutral element). This also results in and inverses of each other with respect to the point addition. If P=Q then it is a point doubling.

Doubling a point

For the point duplication (addition of a point to itself) of a point $P=(x_{P},y_{P})$ one distinguishes two cases.

Case 1: $y_{P}\neq 0$

$P+P=R=(x_{R},y_{R})$
$s=(3x_{P}^{2}+a)/(2y_{P})$ . Here taken from the curve equation ( $y^{2}=x^{3}+ax+b$ ).
$x_{R}=s^{2}-2x_{P}$
$y_{R}=-y_{P}+s(x_{P}-x_{R})$

The only difference to the addition of two different points is the calculation of the slope.

Case 2: $y_{P}=0$

$P+P=\infty$

Because of $y_{P}=0\Rightarrow P=(-P)$ is clear that is inverse to itself.

Calculation rules for the "addition" of points of the curve

Analytical description via the coordinates:

two different points,
$P=(x_{P},y_{P}),$
$Q=(x_{Q},y_{Q}),$
$x_{P}\neq x_{Q},$
the addition of two points and
$\infty$ the neutral element (also called infinity point).

The following rules apply:

$P+Q=Q+P$
$P+(-P)=\infty$
$P+\infty =P$
$-P=(x_{P},-y_{P})$
$(P+Q)+R=P+(Q+R)$

Scalar multiplication of a point

The scalar multiplication $n\cdot P$ simply the repeated addition of this point.

$n\cdot P=P+\dotsb +P$

This multiplication can be solved efficiently with the help of an adapted square & multiply method.

For an elliptic curve over the finite body $\mathrm {GF} (q)$ the point addition runs computationally in an analogous way to the calculation over but the $\mathbb {R}$ coordinates are calculated via $\mathrm {GF} (q)$ .

Addition on the elliptic curve y^2 = x^3 + 1

Elliptic curves over the complex numbers

If, as usual, the complex numbers are interpreted as elements of the Gaussian number plane, elliptic curves over the complex numbers represent a two-dimensional surface embedded in the four-dimensional ${\mathbb {C}}^{2}$ . Although such surfaces elude visualisation, statements can nevertheless be made about their shape, such as the gender of the surface, in this case (torus) of gender 1.

Complex Tori

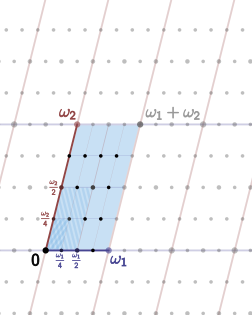
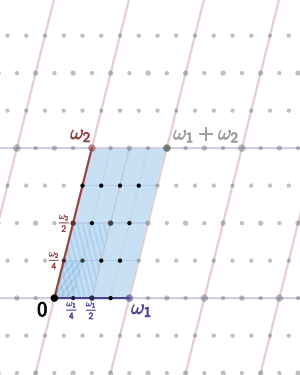
Let Γ be $\Gamma$ a (complete) grid in the complex number plane $\mathbb {C}$ . The factor group ${\mathbb C}/\Gamma$ a one-dimensional abelian compact complex Lie group which is isomorphic as a real Lie group to the torus $S^{1}\times S^{1}$ . For an illustration, one can $\Gamma$ choose producers v,w of Γ ; the quotient ${\mathbb C}/\Gamma$ then obtained from the basic mesh

$\{\lambda v+\mu w\mid 0\leq \lambda ,\ \mu \leq 1\}$ ,

by gluing opposite sides together.

Reference to plane cubes

The functions that parameterise elliptic curves form a large family and have special properties. Since they are defined on a plane and not just on a number line, they can even be required to have periodicity in two directions simultaneously. These functions are also called p-functions. One uses for them the designation $\wp (z)$ where for the complex parameter the designation is more usual than

If Γ is $\Gamma$ a lattice in the complex number plane, the associated Weierstrass ℘-function and its derivative define an embedding

${\mathbb C}/\Gamma \to {\mathbb P}^{2}({\mathbb C}),\quad z\mapsto (1:\wp (z):\wp '(z))$ ,

whose image is the non-singular cubic

$y^{2}=4x^{3}-g_{2}(\Gamma )x-g_{3}(\Gamma )$

is. Every non-singular plane cubic is isomorphic to a cubic created in this way.

In contrast to the sine or cosine, functions are even double-periodic, as can be seen in this picture

It is only decisive for each -function which values it takes on a period mesh. In all directions the outputs will repeat. Therefore, such a mesh forms the parameter set for an elliptic curve.

The mesh can be deformed into a donut as follows. Because of periodicity, opposite sides can be glued together since the parameters there provide the same points on the curve. It can be argued that there is a perfect 1:1 relationship between points on the periodic mesh and the elliptic curve, making it legitimate to think of an elliptic curve as a perfect donut surface.

Also analogous to sine and cosine, one finds that the coordinate $x=\wp (z)$ associated with is the derivative of $\wp (z)$ i.e. $y=\wp '(z)$ . This is again a double-periodic function and it holds $\wp '(z)^{2}=4\wp (z)^{3}+a\wp (z)+b$ (here there is still a 4 in front of the , but this can be eliminated by transformations). This equation resembles $\sin(z)^{2}+\cos(z)^{2}=1$ and can be justified by the approach $\wp '(z)^{2}-4\wp (z)^{3}-a\wp (z)-b=0$ can be shown that the left function is bounded on the periodic mesh and has a zero, and it then already follows from a theorem of function theory by means of double periodicity that it constantly takes the value 0.

In this procedure, care must be taken that the choice of the p-function (and thus the choice of the appropriate period mesh) depends crucially on the numbers and in the equation $y^{2}=4x^{3}+ax+b$

The elliptic function is defined by its Weierstrass form in a lattice Γ $\Gamma$ the complex plane, since the function is doubly periodic (periods ω $\omega _{1}$ , ω $\omega_2$ , both complex numbers, $r\cdot \omega _{1}\neq \omega _{2}$ for a real ). The edges of the lattice are identified, which geometrically results in a torus. By the above mapping, the lattice is mapped into the complex projective plane and the addition of points in the quotient space (torus) $\mathbb {C} /\Gamma$ transfers as a group homomorphism to the elliptic curve in the projective plane, giving the "addition law" of points on the curve explained above.

Points of finite order in the grid are called torsion points. A torsion point of -th order corresponds to the points

${\frac {k}{n}}\omega _{1}+{\frac {l}{n}}\omega _{2}$

with $k,l=0,\dotsc ,n-1$ . In the figure the case n=4 shown. With respect to the addition law defined above for points on elliptic curves, for an -torsion point the equation $n\cdot P=\infty$ .

Classification

Two one-dimensional complex tori ${\mathbb C}/\Gamma _{1}$ and ${\mathbb C}/\Gamma _{2}$ for lattices Γ $\Gamma _{1},\Gamma _{2}$ are isomorphic (as complex Lie groups) if and only if the two lattices are similar, i.e. emerge from each other by a rotational stretch. i.e. emerge from each other by a rotational stretching. Each lattice is similar to a lattice of the form ⟨ $\langle 1,\tau \rangle _{{{\mathbb Z}}}$ similar, where τ $\tau$ is an element of the upper half-plane $\mathbb {H} =\{z\in \mathbb {C} \mid \operatorname {Im} z>0\}$ ; if v , are v,w producers, then τ can be w/v chosen $\tau$ v / or w v/w / The different choices for producers correspond to the operation of the group ${\mathrm {SL}}_{2}({\mathbb Z})$ on the upper half-plane given by

${\begin{pmatrix}a&b\\c&d\end{pmatrix}}\tau ={\frac {a\tau +b}{c\tau +d}}$

is given (moduli group). Two elements τ $\tau _{1},\tau _{2}$ the upper half-plane define isomorphic elliptic curves ${\mathbb C}/\langle 1,\tau _{1}\rangle$ and ${\mathbb C}/\langle 1,\tau _{2}\rangle$ , if τ $\tau _{1}$ and τ $\tau _{2}$ in the same ${\mathrm {SL}}_{2}({\mathbb Z})$ orbit; the set of isomorphism classes of elliptic curves thus corresponds to the orbit space

$\mathrm {SL} _{2}(\mathbb {Z} )\backslash \mathbb {H} ;$

this space is bijectively mapped by the a moduli function, onto $\mathbb {C}$ ; the value of the -function is equal to the -invariants of the cubic given above.

An elliptic curve is defined in the complex plane by an elliptic function over its values in a grid Γ which $\Gamma$ $\omega_2$ is spanned by the complex periods ω $\omega _{1}$ and ω Also drawn are the fourth-order torsion points corresponding to $1/4\ \Gamma$ a grid

Elliptic curves over the rational numbers

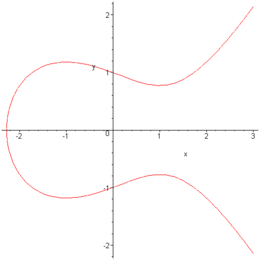
The addition of points of elliptic curves makes it possible to calculate further solutions from simple (guessed) solutions of a cubic equation, which usually have much larger numerators and denominators $(n^{2},n^{3})$ than the initial solutions (and would therefore hardly be found by systematic trial and error).

For example, for the elliptic curve defined over $\mathbb {Q}$ defined elliptic curve

$y^{2}=x^{3}-63$

one finds by guessing the solution $P=(x,y)=(4,1)$ and from this by addition on the elliptic curve the solution 2P=(568,-13537) as well as by further addition on the elliptic curve then still considerably "larger" solutions. This results from

h(2P)=4h(P)+O(1)

for points with integer coordinates on elliptic curves over $\mathbb {Q}$ using the coordinate form of the addition law (see above). Here the $h(x,y)=\log(\mid x\mid )$ height defined for integer points by

The group of rational points on including ${\mathcal O}$ is the Mordell-Weil group $E(\mathbb {Q} )$ . By Mordell-Weil's theorem, is $E(\mathbb {Q} )$ finitely generated and it holds that $E(\mathbb {Q} )=\mathbb {T} \times \mathbb {Z} ^{r}$ where $\mathbb {T} =E(\mathbb {Q} )_{tors}$ are the torsion subgroups and denotes the (algebraic) rank of the elliptic curve. Thus, any point $P=n_{1}P_{1}+...+n_{r}P_{r}+Q$ with fixed $P_{1},\ldots ,P_{r}$ as well as be written from a finite solution set. More generally for a body the group denotes $E(K)[N]$ all K-rational points whose order is a divisor of $N \in \mathbb N$ .

According to the theorem of Lutz and Nagell (Élisabeth Lutz, Trygve Nagell, mid 1930s), for the torsion points, i.e. the points P = (x,y) finite order (i.e. the elements of the torsion subgroups), it holds that $x,y\in \mathbb {Z}$ and either y=0 (then is of order 2) or $y^{2}\mid D$ that is, $y^{2}$ divides (where is the discriminant). This allows the torsion subgroups ${\mathbb T}$ calculated.

The possible torsion subgroups for elliptic curves over the rational numbers were classified by Barry Mazur in a difficult proof (Mazur's theorem (Elliptic Curves)). According to this, for a point of order the number can take one of the values 1 to 10 or 12.

With the theorem of Lutz and Nagell and that of Mazur one has an algorithm for determining the elements P=(x,y) the torsion group ${\mathbb T}$ of an elliptic curve $y^{2}=f(x)$ over the rational numbers $\mathbb {Q}$ :

Find $y^{2}\mid D$ with discriminant D of the curve.
Determine the associated from the equation of the curve and thus have the coordinates of .
Calculate $nP$ with $n=1,\dotsc ,10,12$ (according to Mazur's theorem), if $nP={\mathcal {O}}$ (using here the notation ${\mathcal O}$ for the neutral element), one has a torsion point. If, on the other hand, $nP$ has no integer coordinates, it does not belong to the torsion points.

Elliptic curves, according to Mordell's conjecture (Faltings' theorem, they correspond there to the case of the gender g=1 ) they occupy a special position, they can have infinitely many (rank not equal to zero) or finitely many rational solutions (torsion subgroups). Curves with g>1 , on the other hand, only finitely many solutions. In the case g = 0 there are no or infinitely many solutions (for example, in the case of the circle, infinitely many Pythagorean triples).

The theory of elliptic curves over the body of rational numbers is an active field of research in number theory (arithmetic algebraic geometry) with some famous open conjectures such as the conjecture of Birch and Swinnerton-Dyer which makes a statement about the analytic behaviour of the Hasse-Weil L(E,s) an elliptic curve whose definition involves the number of points of the curve over finite bodies. According to the conjecture in its simplest form, the rank of the elliptic curve is equal to the order of the zero of L(E,s) at s=1 .

Elliptic curves over finite bodies

Instead of over the rational numbers, one can also consider elliptic curves over finite bodies. In this case, the plane, or more precisely the projective plane, in which the elliptic curve lies, consists only of finitely many points. Therefore, the elliptic curve itself can also contain only finitely many elements, which can simplify many considerations. For the number of points of an elliptic curve over a body with elements Helmut Hasse (1936) showed the estimation (Riemann conjecture)

$|N - (q+1)| \le 2 \sqrt{q}$

thus proving an assumption made in Emil Artin's dissertation (1924).

More generally, from the Weil conjectures (a series of conjectures on the Hasse-Weil zeta function, proved in the 1960s and 1970s) for the number $N_{m}$ of points of over a body extension with $q^{m}$ elements follows the equation

$N_m = q^m + 1 - \alpha^m - \beta^m$ ,

where α $\alpha$ and β $\beta$ the two zeros of the characteristic polynomial of the Frobenius homorphism ϕ $\phi_q$ on the elliptic curve over $\mathbf{F}_{q^m}$ are. René Schoof (1985) developed the first efficient algorithm for computing $N_{m}$ . This was followed by improvements by A. O. L. Atkin (1992) and Noam Elkies (1990).

Elliptic curves over finite bodies are used, for example, in cryptography (elliptic curve cryptosystem).

The (as yet unproven) conjecture of Birch and Swinnerton-Dyer attempts to obtain statements about certain properties of elliptic curves over the rational numbers by investigating corresponding properties of elliptic curves over finite bodies (so-called "reduced elliptic curves").

Affine points of the elliptic curve $y^{2}=x^{3}-x$ over $\mathbf {F} _{61}$

Hasse-Weil zeta function and L-function for elliptic curves

the elliptic curve over $\mathbb {Q}$ is given by the equation

$y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}$

with integer coefficients $a_{i}$ given. The reduction of the coefficients modulo a prime defines an elliptic curve over the finite body $\mathbb{F}_p$ (except for a finite set of primes for which the reduced curve has singularities and is therefore not elliptic; in this case said to have bad reduction at ).

The zeta function of an elliptic curve over a finite body is the formal power series

$Z(E({\mathbb {F}}_{p}))=\exp \left(\sum {\mathrm {card}}\left[E({{\mathbb F}}_{{p^{n}}})\right]{\frac {T^{n}}{n}}\right).$

It is a rational function of the form

$Z(E({\mathbb {F}}_{p}))={\frac {1-a_{p}T+pT^{2}}{(1-T)(1-pT)}}.$

(This equation defines the coefficient $a_{p}$ if has good reduction at , the definition in the case of bad reduction is different).

The function of over $\mathbb {Q}$ stores this information for all prime numbers . It is defined by

$L(E(\mathbb {Q} ),s)=\prod _{p}\left(1-a_{p}p^{-s}+\varepsilon (p)p^{1-2s}\right)^{-1}$

with ε $\varepsilon (p)=1$ if has good reduction at , and ε $\varepsilon (p)=0$ otherwise.

The product converges for Hasse conjectured (Riemann conjecture for elliptic curves) that the -function has an analytic continuation on the entire complex plane and L(E,2-s) satisfies a functional equation with a relation between L(E,s) and Hasse's conjecture was proved in 1999 as a consequence of the proof of the modularity theorem. This states that every elliptic curve over $\mathbb {Q}$ is a modular curve (i.e. can be parameterised by modular functions), and for the -functions of modular curves the analytic continuability is known.

Application in cryptography

→ Main article: Elliptic Curve Cryptography

The US foreign intelligence agency NSA recommended in January 2009 that encryption on the internet be switched from RSA to ECC (Elliptic Curve Cryptography) by 2020.

ECC is a public-key cryptosystem (or asymmetric cryptosystem) in which, unlike a symmetric cryptosystem, the communicating parties do not need to know a common secret key. Asymmetric cryptosystems in general work with trapdoor functions, i.e. functions that are easy to calculate but virtually impossible to invert without a secret (the "trapdoor").

Elliptic curve encryption works in principle by assigning the elements of the message to be encrypted (i.e. the individual bits) in some way to the points a (fixed) elliptic curve and then n>1 the encryption function $P\mapsto nP$ with a (fixed) natural number . For this procedure to be secure, the decryption function must be $(nP,P)\mapsto n$ difficult to compute.

Since the problem of the discrete logarithm in elliptic curves (ECDLP) is significantly more difficult than the calculation of the discrete logarithm in finite bodies or the factorisation of integers, cryptosystems based on elliptic curves - with comparable security - manage with considerably shorter keys than the conventional asymmetric crypto methods, such as the RSA cryptosystem. The currently fastest algorithms are the Babystep-Giantstep algorithm and the Pollard-Rho method, whose runtime is $O\left(2^{n/2}\right)$ where the bit length of the size of the underlying body.

Elliptic curve

History

Affine and projective plane

Definition

Isomorphic elliptic curves

Definition

Short Weierstrass equation

Examples

Group operation

Geometric interpretation

Addition of two different points

Doubling a point

Calculation rules for the "addition" of points of the curve

Scalar multiplication of a point

Elliptic curves over the complex numbers

Complex Tori

Reference to plane cubes

Classification

Elliptic curves over the rational numbers

Elliptic curves over finite bodies

Hasse-Weil zeta function and L-function for elliptic curves

Application in cryptography

Search by letter