Ellipsoid

An ellipsoid is the 3-dimensional equivalent of an ellipse. Just as an ellipse can be conceived as an affine image of the unit circle, applies:

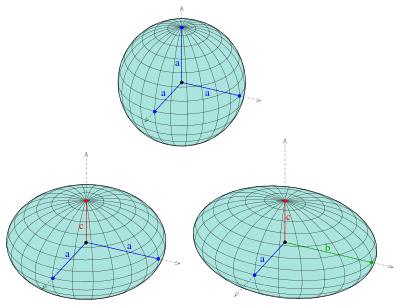
An ellipsoid (as a surface) is an affine image of the unit sphere $x^{2}+y^{2}+z^{2}=1.$

The simplest affine mappings are the scalings of Cartesian coordinates. They provide ellipsoids with equations

$E_{abc}\colon \quad {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1,\quad a,b,c>0.$

Such an ellipsoid is point-symmetric with respect to the point (0,0,0) , the center of the ellipsoid. The numbers a,b,c are, analogously to an ellipsesemi-axes of the ellipsoid and the points $(\pm a,0,0),(0,\pm b,0),(0,0,\pm c)$ its 6 vertices.

If , the ellipsoid is a sphere.
If exactly two semi-axes coincide, the ellipsoid is a rotational ellipsoid.
If the 3 semi-axes are all different, the ellipsoid is called triaxial or triaxial.

All ellipsoids $E_{abc}$ are symmetric with respect to each of the three coordinate planes. In the case of a rotational ellipsoid, rotational symmetry with respect to the axis of rotation is added. A sphere is symmetric to each plane through the center.

Approximate examples of rotational ellipsoids are the rugby ball and oblate rotating celestial bodies, such as the Earth or other planets (Jupiter), suns, or galaxies. Elliptical galaxies and dwarf planets (e.g. (136108) Haumea) can also be triaxial.

In linear optimization, ellipsoids are used in the ellipsoid method.

Jupiter's diameter from pole to pole is much smaller than at the equator (red circle for comparison)

Sphere (top, a=4 ),
rotational
ellipsoid
(bottom left, $a=b=5,\ c=3$ ),
triaxial ellipsoid (bottom right, $a=4{,}5,\ b=6,\ c=3$ )

Parameter representation

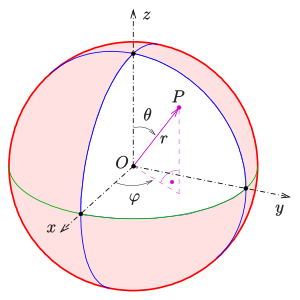
The points on the unit sphere can be parameterized as follows (see Sphere coordinates):

${\begin{array}{cll}x&=&\sin \theta \cdot \cos \varphi \\y&=&\sin \theta \cdot \sin \varphi \\z&=&\cos \theta \end{array}}$

For the angle θ $\theta$ (measured from the z-axis) $0\leq \theta \leq \pi$ . For the angle φ $\varphi$ (measured from the x-axis) holds

Scaling the individual coordinates with the factors a,b,c , we get a parameter representation of the ellipsoid $E_{abc}$ :

${\begin{array}{cll}x&=&a\cdot \sin \theta \cdot \cos \varphi \\y&=&b\cdot \sin \theta \cdot \sin \varphi \\z&=&c\cdot \cos \theta \end{array}}$

where $0\leq \theta \leq \pi$ and $0\leq \varphi <2\pi .$

Spherical coordinates $r,\theta ,\varphi$ of a point and Cartesian coordinate system.

Volume

The volume of the ellipsoid $E_{abc}$ is

$V={\frac {4}{3}}\pi abc.$

A sphere with radius has volume $V={\tfrac {4}{3}}\pi r^{3}.$

Derivation

The intersection of the ellipsoid $E_{abc}$ with a plane of height is the ellipse ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1-{\frac {z^{2}}{c^{2}}}$ with the semi-axes

$a'=a{\sqrt {1-{\frac {z^{2}}{c^{2}}}}},\ b'=b{\sqrt {1-{\frac {z^{2}}{c^{2}}}}}$ .

The area of this ellipse is $A(z)=\pi a'b'=\pi ab(1-{\frac {z^{2}}{c^{2}}})$ . The volume is then given by

$\int _{-c}^{c}A(z)\ \mathrm {d} z=\pi ab\int _{-c}^{c}(1-{\frac {z^{2}}{c^{2}}})\ \mathrm {d} z={\frac {4}{3}}\pi abc.$

Surface

Surface of an ellipsoid of revolution

→ Main article: Rotational ellipsoid

The surface of an oblate ellipsoid of revolution $E_{aac}$ with

$A=2\pi a\left(a+{\frac {c^{2}}{\sqrt {a^{2}-c^{2}}}}\,\operatorname {arsinh} \left({\frac {\sqrt {a^{2}-c^{2}}}{c}}\right)\right),$

that of the extended ellipsoid (

$A=2\pi a\left(a+{\frac {c^{2}}{\sqrt {c^{2}-a^{2}}}}\,\operatorname {arcsin} \left({\frac {\sqrt {c^{2}-a^{2}}}{c}}\right)\right).$

A sphere with radius has surface $A=4\pi r^{2}$ .

Surface of a triaxial ellipsoid

The surface area of a triaxial ellipsoid cannot be expressed using functions which are considered elementary, such as $\operatorname {arsinh}$ or $\arcsin$ above for the rotational ellipsoid. Adrien-Marie Legendre succeeded in calculating the area using elliptic integrals. Let If one writes

$k={\frac {a}{b}}{\frac {\sqrt {b^{2}-c^{2}}}{\sqrt {a^{2}-c^{2}}}}$ and φ $\varphi =\arcsin {\frac {\sqrt {a^{2}-c^{2}}}{a}},$

the integrals are

$E(k,\varphi )=\int _{0}^{\sin \varphi }{\sqrt {\frac {1-k^{2}x^{2}}{1-x^{2}}}}\ \mathrm {d} x$ and $F(k,\varphi )=\int _{0}^{\sin \varphi }{\frac {1}{{\sqrt {1-x^{2}}}{\sqrt {1-k^{2}x^{2}}}}}\ \mathrm {d} x.$

The surface has with and according to Legendre the value

$A=2\pi c^{2}+{\frac {2\pi b}{\sqrt {a^{2}-c^{2}}}}\left(c^{2}F(k,\varphi )+(a^{2}-c^{2})E(k,\varphi )\right).$

If the expressions for and φ $\varphi$ as well as the substitutions

and $u:={\frac {\sqrt {a^{2}-c^{2}}}{a}}$ $v:={\frac {\sqrt {b^{2}-c^{2}}}{b}}$

into the equation for , we get the notation

$A=2\pi c^{2}+2\pi ab\int _{0}^{1}{\frac {1-u^{2}v^{2}x^{2}}{{\sqrt {1-u^{2}x^{2}}}{\sqrt {1-v^{2}x^{2}}}}}\ \mathrm {d} x.$

From Knud Thomsen comes the integral-free approximation formula

$A\approx 4\pi \left({\frac {(ab)^{\frac {8}{5}}+(ac)^{\frac {8}{5}}+(bc)^{\frac {8}{5}}}{3}}\right)^{\frac {5}{8}}.$

The maximum deviation from the exact result is less than 1.2%.

In the limiting case of a completely flattened ellipsoid $\left(c\to 0\right)$ all three given formulas for tend to $2\pi ab,$ twice the value of the area of an ellipse with semiaxes and .

Application example to the formulas

The planet Jupiter is much flatter at the poles than at the equator because of the centrifugal forces acting due to the fast rotation and have approximately the shape of a rotational ellipsoid.

Jupiter has the equatorial diameter 142984 km and the pole diameter 133708 km. So for the semi-axes $a=b=71492\ \mathrm {km}$ and $c=66854\ \mathrm {km}$ . The mass of Jupiter is about 1.899 - 1027 kg. From this, using the above formulas for volume, mean density, and surface area:

Volume: $V={\frac {4}{3}}\cdot \pi \cdot a\cdot b\cdot c\approx 1{,}4313\cdot 10^{15}\ \mathrm {km^{3}}$

This is about 1321 times the volume of the Earth.

Mean density: $\rho ={\frac {m}{V}}={\frac {1{,}899\cdot 10^{27}\ \mathrm {kg} }{1{,}4313\cdot 10^{15}\ \mathrm {km^{3}} }}={\frac {1{,}899\cdot 10^{27}\ \mathrm {kg} }{1{,}4313\cdot 10^{24}\ \mathrm {m^{3}} }}\approx 1327\ \mathrm {kg} /\mathrm {m^{3}}$

Jupiter thus has a slightly higher density overall than water under standard conditions.

Surface: $A\approx 4\cdot \pi \cdot \left({\frac {(a\cdot b)^{\frac {8}{5}}+(a\cdot c)^{\frac {8}{5}}+(b\cdot c)^{\frac {8}{5}}}{3}}\right)^{\frac {5}{8}}\approx 6{,}15\cdot 10^{10}\ \mathrm {km^{2}}$

This is about 121 times the surface area of the Earth.

Plane cuts

Features

The intersection of an ellipsoid with a plane is

an ellipse if it contains at least two points,
a point if the plane is a tangent plane,
otherwise empty.

The first case follows from the fact that a plane intersects a sphere in a circle and a circle turns into an ellipse in an affine mapping. That some of the intersecting ellipses are circles is obvious in the case of a rotational ellipsoid: all plane intersections which contain at least 2 points and whose planes are perpendicular to the axis of rotation are circles. But that also every 3-axis ellipsoid contains many circles is not obvious and is explained in Circle Section Plane.

The true outline of any ellipsoid is a plane section, i.e. an ellipse, for both parallel projection and central projection (see pictures).

Determination of a cutting ellipse

Given: Ellipsoid $\ {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1\$ and a plane with equation $\ n_{x}x+n_{y}y+n_{z}z=d\ ,$ which intersects the ellipsoid in an ellipse.
Wanted: Three vectors ${\vec {f}}_{0}$ (center point) and ${\vec {f}}_{1},\;{\vec {f}}_{2}$ (conjugate vectors) such that the intersection ellipse through the parameter representation is

${\vec {x}}={\vec {f}}_{0}+{\vec {f}}_{1}\cos t+{\vec {f}}_{2}\sin t\quad$

can be described (see ellipse).

Solution: Scaling $\ u={\frac {x}{a}}\ ,\ v={\frac {y}{b}}\,\ w={\frac {z}{c}}\$ transforms the ellipsoid into the unit sphere $u^{2}+v^{2}+w^{2}=1\$ and the given plane into the plane with equation $\ n_{x}au+n_{y}bv+n_{z}cw=d\$ Let the Hessian normal form of the new plane be $\ m_{u}u+m_{v}v+m_{w}w=\delta \$ with normal unit vector $\;{\vec {m}}=(m_{u},m_{v},m_{w})^{T}\;.$ Then the
center of the intersection circle is ${\vec {e}}_{0}=\delta \;{\vec {m}}\;$ and its radius is ρ $\;\rho ={\sqrt {1-\delta ^{2}}}\;.$
If $\ m_{w}=\pm 1\$ , let $\quad {\vec {e}}_{1}=(\rho ,0,0)^{T}\;,\ {\vec {e}}_{2}=(0,\rho ,0)^{T}\;.$ (The plane is horizontal!)
If $\ m_{w}\neq \pm 1$ , let $\quad {\vec {e}}_{1}=\rho \,{\frac {(m_{v},-m_{u},0)^{T}}{\sqrt {m_{u}^{2}+m_{v}^{2}}}}\;,\ {\vec {e}}_{2}={\vec {m}}\times {\vec {e}}_{1}\ .$
The vectors ${\vec {e}}_{1},{\vec {e}}_{2}$ are in each case two orthogonal vectors lying in the intersection plane of length ρ $\rho$ (circle radius), i.e., the intersection circle is $\;{\vec {u}}={\vec {e}}_{0}+{\vec {e}}_{1}\cos t+{\vec {e}}_{2}\sin t\;$ described by the parameter representation

If we now undo the above scaling (affine mapping), the unit sphere becomes the given ellipsoid again and we obtain from the vectors ${\vec {e}}_{0},{\vec {e}}_{1},{\vec {e}}_{2}$ the sought vectors ${\vec {f}}_{0},{\vec {f}}_{1},{\vec {f}}_{2}$ , which can be used to describe the cutting ellipse. How to determine the vertices of the ellipse and thus its semi-axes is explained under Ellipse.

Example: The images belong to the example with $\;a=4,\;b=5,\;c=3\;$ and the intersection plane $\;x+y+z=5\;.$ The image of the ellipsoid section is a perpendicular parallel projection onto a plane parallel to the section plane, i.e., the ellipse appears in true form except for a uniform scaling. Note that not perpendicular to the section plane ${\vec {f}}_{0}$ here, unlike ${\vec {e}}_{0}$ The vectors ${\vec {f}}_{1},\;{\vec {f}}_{2}$ are not orthogonal here unlike ${\vec {e}}_{1},\;{\vec {e}}_{2}\;$

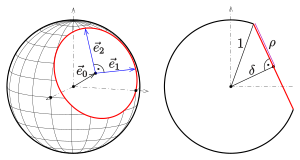
Plane section of the unit sphere

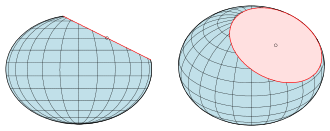
Plane section of an ellipsoid

Thread construction

The thread construction of an ellipsoid is a transfer of the idea of the gardener construction of an ellipse (see figure). A thread construction of a rotational ellipsoid results from the construction of the meridian ellipses with the help of a thread.

Constructing points of a 3-axis ellipsoid using a taut thread is somewhat more complicated. Wolfgang Boehm, in the article Die Fadenkonstruktion der Flächen zweiter Ordnung, attributes the basic idea of the thread construction of an ellipsoid to the Scottish physicist James Clerk Maxwell (1868). Otto Staude then generalized the thread construction to quadrics in papers in 1882, 1886, 1898. The thread construction for ellipsoids and hyperboloids is also described in the book Anschauliche Geometrie by David Hilbert and Stefan Cohn-Vossen. Sebastian Finsterwalder also dealt with this topic in 1886.

Design steps

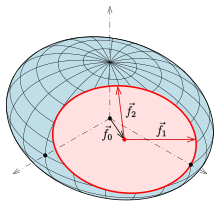
(1) Choose an ellipse and a hyperbola forming a pair of focal conic sections:

Ellipse: $\quad E(\varphi )=(a\cos \varphi ,b\sin \varphi ,0)\$ and

Hyperbola: $\ H(\psi )=(c\cosh \psi ,0,b\sinh \psi )\quad ,\ c^{2}=a^{2}-b^{2}\$

with the vertices and foci of the ellipse

$S_{1}=(a,0,0),\ F_{1}=(c,0,0),\ F_{2}=(-c,0,0),\ S_{2}=(-a,0,0)\;.$

and a thread (red in the figure) of length .

(2) Fix one end of the thread at the vertex $S_{1}$ and the other end at the focal point $F_{2}$ . The thread is held taut at a point such that the thread can slide on the hyperbola from the back and on the ellipse from the front (see figure). The thread passes over that hyperbola point with which the distance from to $S_{1}$ over a hyperbola point becomes minimal. Analogous applies to the thread part from to $F_{2}$ over an ellipse point.

(3) If the point chosen to have positive y and z coordinates, then a point of the ellipsoid with the equation

${\frac {x^{2}}{r_{x}^{2}}}+{\frac {y^{2}}{r_{y}^{2}}}+{\frac {z^{2}}{r_{z}^{2}}}=1\quad$ and

$r_{x}={\frac {1}{2}}(l-a+c)\ ,\quad r_{y}={\sqrt {r_{x}^{2}-c^{2}}}\ ,\quad r_{z}={\sqrt {r_{x}^{2}-a^{2}}}\ .$

(4) the remaining points of the ellipsoid are obtained by suitably looping the thread around the focal cone intersections.

The equations for the semi-axes of the generated ellipsoid are obtained by $Y=(0,r_{y},0),\ Z=(0,0,r_{z})$ dropping the point into the two vertices

From the drawing below you can see that F_1,F_2 are also the foci of the equatorial ellipse. I.e.: The equatorial ellipse is confocal to the given focal ellipse. So $l=2r_{x}+(a-c)$ , which $r_{x}={\frac {1}{2}}(l-a+c)$ gives Furthermore, we see that $r_{y}^{2}=r_{x}^{2}-c^{2}$ .
From the upper drawing it follows that S_1,S_2 are the foci of the ellipse in the x-z plane and it holds that $r_{z}^{2}=r_{x}^{2}-a^{2}$ .

Inversion:
If one wishes to $r_{x},r_{y},r_{z}$ construct
a 3-axis ellipsoid ${\mathcal E}$ given by its equation with the semi-axes parameters necessary for the thread construction can be $a,b,l$ calculated from the equations in step (3). For the following considerations the equations are important

(5) $:\ r_{x}^{2}-r_{y}^{2}=c^{2},\quad r_{x}^{2}-r_{z}^{2}=a^{2},\quad r_{y}^{2}-r_{z}^{2}=a^{2}-c^{2}=b^{2}\ .$

Confocal ellipsoids:
If ${\mathcal {\overline {E}}}$
is an ellipsoid confocal to ${\mathcal E}$ with the squares of the semiaxes

(6) $:\ {\overline {r}}_{x}^{2}=r_{x}^{2}-\lambda ,\quad {\overline {r}}_{y}^{2}=r_{y}^{2}-\lambda ,\quad {\overline {r}}_{z}^{2}=r_{z}^{2}-\lambda \;,$

so one recognizes from the previous equations that the focal cone sections belonging to ${\mathcal {\overline {E}}}$ have the same semiaxes a,b,c as those of ${\mathcal E}$ for the thread generation. Therefore, analogous to the role of the foci in the filament generation of an ellipse, the focal conic sections of a 3-axis ellipsoid are taken to be its infinitely many foci and are called focal curves of the ellipsoid.

converse is also true: If we choose a second thread of length $\overline l$ and set λ $\lambda =r_{x}^{2}-{\overline {r}}_{x}^{2}$ , then ${\overline {r}}_{y}^{2}=r_{y}^{2}-\lambda ,\ {\overline {r}}_{z}^{2}=r_{z}^{2}-\lambda \;.$ I.e.: The two ellipsoids are confocal.

Boundary case rotational ellipsoid:
In the case a=c $\ S_{1}=F_{1},\;S_{2}=F_{2}\;$ , i.e., the focal ellipse degenerates into a line and the hyperbola into two rays on the x-axis. The ellipsoid is then a rotational ellipsoid with the x-axis as the axis of rotation. It is $\ r_{x}={\tfrac {l}{2}},\;r_{y}=r_{z}={\sqrt {r_{x}^{2}-c^{2}}}\$ .

Properties of the focal hyperbola:If
one observes an ellipsoid from an outside point on the associated focal hyperbola, the outline of the ellipsoid appears as a circle. Or, put another way, the tangents of the ellipsoid through form a perpendicular circular cone whose axis of rotation is tangent in to the hyperbola. Letting the eye point run to infinity, the view of a perpendicular parallel projection with an asymptote of the focal hyperbola as projection direction is created. The true outline curve on the ellipsoid is generally not a circle.
In the figure, a parallel projection of a 3-axis ellipsoid (semi-axes: 60,40,30) in the direction of an asymptote is shown in the lower left, and a central projection with center on the focal hyperbola and principal point on the tangent to the hyperbola in shown in the lower right. In both projections the apparent outlines are circles. On the left, the image of the coordinate origin the center of the outline circle; on the right, the principal point is the center.

The focal hyperbola of an ellipsoid intersects the ellipsoid at its four umbilical points.

Property of the focal ellipse:
The focal ellipse with its interior can be considered as
the interface of
the set of confocal ellipsoids determined
by a,b
$\;r_{z}\to 0\;$ as an infinitely thin ellipsoid. It is then
$\;r_{x}=a,\;r_{y}=b,\;l=3a-c\;.$

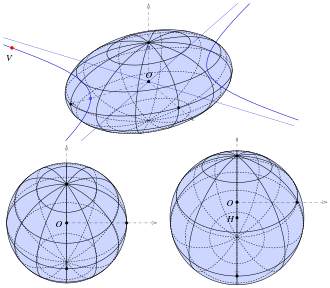
Below: Parallel projection and central projection of a 3-axis ellipsoid where the apparent outline is a circle.

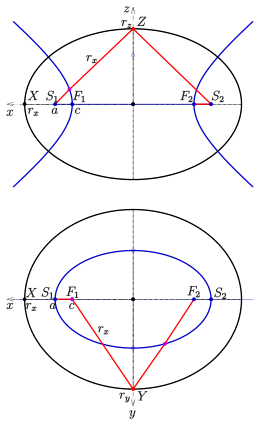
Thread construction: Determination of the semi-axes

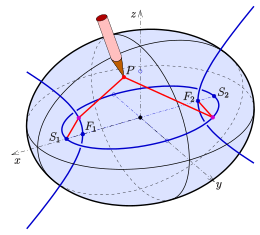
Thread construction of an ellipsoid

Fade construction of an ellipse
$|S_{1}S_{2}|=$ length of the fade (red)

Ellipsoid in any position

Parameter representation

An affine mapping can be described by a parallel shift around ${\vec {f}}_{0}$ and a regular 3×3 matrix

${\vec {x}}\mapsto {\vec {f}}_{0}+A{\vec {x}}={\vec {f}}_{0}+x{\vec {f}}_{1}+y{\vec {f}}_{2}+z{\vec {f}}_{3}$ ,

where ${\vec {f}}_{1},{\vec {f}}_{2},{\vec {f}}_{3}$ are the column vectors of the matrix

The parameter representation of any ellipsoid results from the above parameter representation of the unit sphere and the description of an affine mapping:

${\vec {x}}(\theta ,\varphi )={\vec {f}}_{0}+{\vec {f}}_{1}\cos \theta \cos \varphi +{\vec {f}}_{2}\cos \theta \sin \varphi +{\vec {f}}_{3}\sin \theta ,\quad -\pi /2\leq \theta \leq \pi /2,\ 0\leq \varphi <2\pi$

Conversely, if one chooses a vector ${\vec {f}}_{0}$ arbitrarily and the vectors ${\vec {f}}_{1},{\vec {f}}_{2},{\vec {f}}_{3}$ arbitrarily but linearly independent, the above parameter representation describes an ellipsoid in every case. If the vectors form ${\vec {f}}_{1},{\vec {f}}_{2},{\vec {f}}_{3}$ an orthogonal system, then the points ${\vec {f}}_{0}\pm {\vec {f}}_{i},\ i=1,2,3$ the vertices of the ellipsoid and $|{\vec {f}}_{1}|,|{\vec {f}}_{2}|,|{\vec {f}}_{3}|$ the associated semiaxes.

A normal vector at the point ${\vec {x}}(\theta ,\varphi )$ is

${\vec {n}}(\theta ,\varphi )={\vec {f}}_{2}\times {\vec {f}}_{3}\cos \theta \cos \varphi +{\vec {f}}_{3}\times {\vec {f}}_{1}\cos \theta \sin \varphi +{\vec {f}}_{1}\times {\vec {f}}_{2}\sin \theta .$

For a parameter representation of any ellipsoid an implicit description also be F(x,y,z)=0 given. For an ellipsoid with center at the coordinate origin, i.e., ${\vec {f}}_{0}=(0,0,0)^{T}$ , is

$F(x,y,z)=\operatorname {det} ({\vec {x}},{\vec {f}}_{2},{\vec {f}}_{3})^{2}\;+\;\operatorname {det} ({\vec {f}}_{1},{\vec {x}},{\vec {f}}_{3})^{2}\;+\;\operatorname {det} ({\vec {f}}_{1},{\vec {f}}_{2},{\vec {x}})^{2}\;-\;\operatorname {det} ({\vec {f}}_{1},{\vec {f}}_{2},{\vec {f}}_{3})^{2}=0$

an implicit representation.

Remark: The ellipsoid described by the above parameter representation is in the possibly skewed coordinate system ${\vec {f}}_{0}$ (coordinate origin), ${\vec {f}}_{1},{\vec {f}}_{2},{\vec {f}}_{3}$ (basis vectors) the unit sphere.

Ellipsoid as quadric

→ Main article: Quadric

Any ellipsoid with center ${\vec {f}}_{0}$ can be written as the solution set of an equation

$({\vec {x}}-{\vec {f}}_{0})^{\top }A\,({\vec {x}}-{\vec {f}}_{0})=1$

where a positive definite matrix.

The eigenvectors of the matrix determine the major axis directions of the ellipsoid and the eigenvalues of are the reciprocals of the squares of the semi-axes: $a^{-2}$ , $b^{-2}$ and $c^{{-2}}$ .

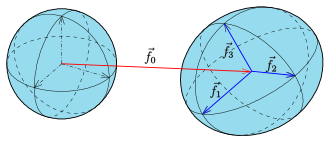
Ellipsoid as affine image of the unit sphere

Ellipsoid in projective geometry

If one closes the 3-dimensional affine space and the individual quadrics projectively by a far plane or far points, the following quadrics are projectively equivalent, i.e., there is in each case a projective collineation which transforms one quadric into the other:

Ellipsoid, elliptical paraboloid, and 2-shell hyperboloid.

Ellipsoid

Parameter representation

Volume

Surface

Surface of an ellipsoid of revolution

Surface of a triaxial ellipsoid

Application example to the formulas

Plane cuts

Features

Determination of a cutting ellipse

Thread construction

Ellipsoid in any position

Parameter representation

Ellipsoid as quadric

Ellipsoid in projective geometry

See also

Search by letter