Ellipse
![]()
This article is about the geometric figure of the ellipse, for other meanings see Ellipse (disambiguation). For the algebraic curve, see Elliptic curve.
Ellipses are special closed oval curves in geometry. They belong to the conic sections along with the parabolas and the hyperbolas. An illustrative definition uses the property that the sum of the distances of an ellipse point from two given points, the foci, is the same for all points. If the foci are identical, you get a circle.
Every ellipse can be 



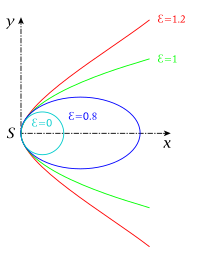
The ellipse (from Greek ἔλλειψις élleipsis 'defect') was introduced and named by Apollonios of Perge (c. 262-190 BC), the name referring to the eccentricity ε
Ellipses do not only occur as plane sections of a cone. There are also ellipses on cylinders, ellipsoids, hyperboloids and elliptic paraboloids.
In nature, ellipses occur in the form of undisturbed Keplerian planetary orbits around the sun. Ellipses are also often needed when drawing oblique images, since a circle is generally mapped onto an ellipse by a parallel projection (see Ellipse (Descriptive Geometry)).
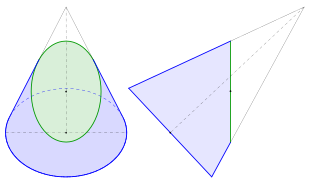
Ellipse as a conic section. The central axis of the cone is inclined so far that the ellipse appears in true size in the side view from the right.

Saturn's rings appear elliptical.
Definition of an ellipse as a geometric place
There are different ways to define ellipses. Besides the usual definition by certain distances of points, it is also possible to define an ellipse as an intersection curve between a corresponding inclined plane and a cone (see 1st picture) or as an affine image of the unit circle.
An ellipse is the geometric locus of all points 





To exclude a distance, assume that 



The center 









The equation 








With the help of Dandelin spheres one proves that holds:
Any intersection of a cone with a plane that does not contain the apex of the cone and whose slope is less than that of the cone's generatrices is an ellipse.
Due to the guide circle property, an ellipse is the equidistance curve to each of its foci and the guide circle with the other focal point as the center.
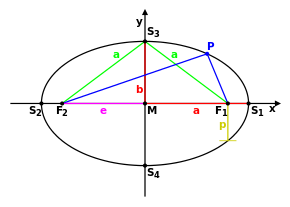
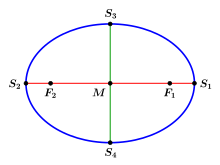
This graphic shows the designations used in the following text
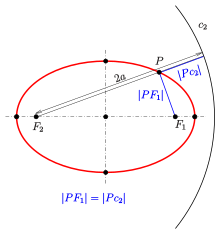
Ellipse: definition with guide circle
Ellipse in Cartesian coordinates
Equation
A. Introduce Cartesian coordinates such that the center of the ellipse is at the origin, the 
the foci are the points 
the main vertices 
so for any point 




After removing the roots by suitable squaring and using the relation 





From this still result the relations
If 

If 

B. The ellipse in A. can also be written using a bilinear form as the solution set of the equation 






C. An ellipse with the center at the origin and the foci on the 



Due to the definition of an ellipse holds:
An ellipse is symmetrical about its axes and therefore also about its center.
(The symmetry property can also be easily seen in the equation of an ellipse derived here).
Half parameter
Half the length 


is valid. The half parameter has the additional meaning (see below): The radius of curvature in the main vertices is 
Tangent
A. For the major vertex 





and thus the point-slope form of the tangent line at the point 
Considering 

This form also includes the tangents through the main vertices. The latter also applies to the vector form

B. The tangent equation 





this gives the direction vector of the vector shape given in A. and also the slope of the point slope shape given there.
A graphical determination of elliptic tangents can be found in the article Ellipse (Descriptive Geometry).
Equation of a displaced ellipse
If we move the above ellipse so that the center 
Parameter representations
Standard display
The usual parameter representation of an ellipse uses the sine and cosine function. Because of 
the ellipse
Different ways of interpreting the parameter 
Rational parameter representation
With the substitution 
and thus the rational parameter representation of an ellipse:
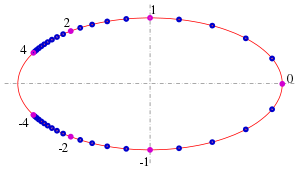
The rational parameter representation has the following properties (see figure):
- For
the main positive vertex is shown:
; for
the minor positive vertex:
.
- Transition to the opposite number of the parameter reflects the represented point on the
axis:
;
- Transition to the inverse of the parameter reflects the represented point on the
axis:
.
- The negative principal vertex cannot be
represented with any real parameter The coordinates of the same are the limits of the parameter representation for infinite positive or negative
:
.
Rational parameter representations of conic sections (ellipse, hyperbola, parabola) play an important role in CAD for quadratic rational Bezier curves.
Tangent slope as parameter
A parameter representation using the tangent slope 

With the help of trigonometric formulas we get
Replacing 

Here 



The equation of the tangent at the point 




This main form of the tangent equation is an essential tool in determining the orthoptic curve of an ellipse.
Remark. The main form of the tangent equation and the coordinates of 
Displaced ellipse
A displaced ellipse with center 
described.
A parameter representation of an arbitrary ellipse is given in the section Ellipse as an affine image of the unit circle.
Properties
Focal Point Property
→ Main article: Focal point (geometry)
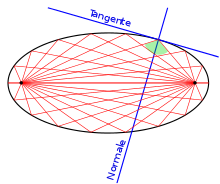
The connecting line between a focal point and a point of the ellipse is called focal line, guide ray or focal ray. Focal points and focal rays got their name because of the following property:
The angle between the two focal rays at one point of the ellipse is bisected by the normal at that point.
Applications
- The angle of incidence formed by one focal ray with the tangent is equal to the angle of reflection formed by the tangent with the other focal ray. A light beam that originates from one focal point is thus reflected at the elliptical tangent in such a way that it hits the other focal point. In the case of an elliptical mirror, all light rays emanating from one focal point therefore meet at the other focal point.
- Since all paths from one focal point to the other (along associated focal rays) are of equal length, sound, for example, is "amplified" by constructive interference.
- The tangent at the ellipse point is the bisector of the exterior angle. Since angle bisectors are easy to construct, the focal point property provides a simple method to construct the tangent at an ellipse point (Another tangent construction is described in Ellipse (Descriptive Geometry)).
Two ellipses with the same foci 

Proof of the focal point property
Since the tangent is perpendicular to the normal, the above assertion is proven if the analogous statement holds for the tangent:
The exterior angle of the focal rays 

Let be 








holds. This means that But if 
Remark: A proof by means of analytic geometry is in the proof archive.
Natural occurrence and application in technology:
The ceilings of some caves resemble an ellipse half. If you are - with your ears - in one focal point of this ellipse, you hear any sound whose origin lies in the second focal point amplified ("whispering vault"). This type of sound transmission even works from platform to platform in some stations of the Paris Métro. The same principle of sound focusing is used today to break up kidney stones with shock waves. A reflector in the shape of an ellipse is also used in the lamp-pumped Nd:YAG laser. The pump source - either a flash lamp or an arc lamp - is positioned in one focal point, and the doped crystal is placed in the other focal point.
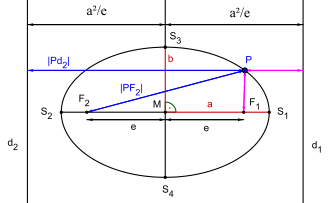
Directrix
For a true ellipse, i.e. 




Proof:
With 


The inverse of this statement is also true and can be used to further define an ellipse (similar to a parabola):
For a point 







The choice ε 
Proof:







The substitution 
This is the equation of an ellipse (

For ε 


which is the equation of an ellipse with center 


General case:
For the focal point 

The right side of the equation uses the Hessian normal form of a straight line to calculate the distance of a point from a straight line.
Guideline construction:
Because of 






Conjugate diameters
- If for any ellipse diameter (of an ellipse chord through the ellipse center) consider
all parallel chords, their centers also lie on an ellipse diameter
. One calls
the
diameter conjugate to
- If we form the conjugate diameter again to the conjugate diameter, we get the original one again. Thus, in the drawing, the diameter conjugate to
coincides with the original diameter
- The tangents in the endpoints of a diameter (say
) are parallel to the conjugate diameter (in the example
).
- Major and minor axes are the only pair of orthogonal conjugate diameters.
- If the ellipse is a circle, exactly the orthogonal diameters are (also) conjugate.
- If conjugate diameters are not orthogonal, the product of their slopes is
.
- Let
,
conjugate diameters. Then
. (Theorem of Apollonius)
Conjugate diameters (primarily of ellipses) are also treated on a separate Wikipedia page, as well as the theorem of Apollonius (including proof). A complete analytical proof of all statements listed here, which starts from the common bilinear form of two lines of origin, can be found in the proof archive. This proof needs neither trigonometric functions nor parameter representations nor an affine mapping.
One possible application in the field of technical drawing is the ability to find the highest point of an ellipse or elliptical arc of any position above a line - useful e.g. for correct 2D representations of non-orthogonal views of cylindrical bodies or rounded edges without using 3D programs. This is important for the clean connection of lines running tangentially away from the ellipse. For this purpose, two chords parallel to the desired tangent direction and the line of the corresponding conjugate diameter defined by the centers of the two chords must be drawn into the ellipse or the elliptical arc. The intersection of this line with the ellipse or the elliptical arc defines the connection point of the tangent (and normally the end point of the elliptical arc).
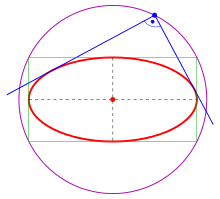
Orthogonal tangents
→ Main article: Orthoptic curve
For the ellipse 

This circle is called the orthoptic curve of the given ellipse, it is the circumcircle of the rectangle circumscribing the ellipse.
Pole-Polar Relationship
If one introduces Cartesian coordinates in such a way that the center of the ellipse lies in the origin, then an arbitrary ellipse can be described with the equation 








Such a relationship between points and lines mediated by a conic section is called a pole-polar relationship or simply polarity. Pole-polar relationships also exist for hyperbolas and parabolas, see also Pole and polar.
The following positional relationships apply to pole and polar:
- The focal point
and the directrix
are polar to each other. Since both are also polar with respect to the vertex circle
, the directrix can also be constructed with the help of compass and ruler (see also circle mirroring). (1)
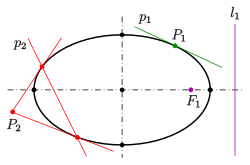
- Exactly when the pole is outside the ellipse, the polar has two points in common with the ellipse (see figure:
). (2)
- Exactly when the pole lies on the ellipse, the polar has exactly one point in common with the ellipse (= the polar is a tangent; see figure:
). (3)
- Exactly when the pole is inside the ellipse, the polar has no point in common with the ellipse (see figure:
). (4)
- Each common point of a polar and an ellipse is a tangent point from the corresponding pole
to the ellipse (see figure:
). (5)
- The intersection of two polars is the pole of the straight line through the poles. (6)
Derivation of the positional relationships of pole and polar; alternative derivation of a tangent and an ellipse equation.
A. If a polar is parallel to the 




Inserting the considered polar curve into the center form of an ellipse results in the condition for the ordinate any 



B. If a polar is not parallel to the 




Inserting the main form 



C. Overall, the term 

- For
the polar no point in common with the ellipse, and the pole lies inside the ellipse. From this follows (2).
- For
polar has exactly one point in common with the ellipse, and the pole lies on the ellipse. So the polar is a tangent to the ellipse, the pole is its point of contact (see figure:
). From this follows (3).
- For the polar
two points in common with the ellipse, and the pole lies outside the ellipse. From this follows (4).
D. If a tangent is not perpendicular, solving the equation 



Substituting 



this parameter representation does not capture the main vertices.
E. Starting from the bilinear form of the ellipse given in the section "Equation", B., the polar to the point 




If 
This coordinate-free computational representation of the polar is suitable for proofs. With the coordinate representations 



Proof of (5) ("Every common point of a polar and an ellipse is a tangent point from the associated pole 
Since the ellipse points 







Proof of (6) ("The intersection of two polars is the pole of the straight line through the poles."):
For an intersection 











the pointwise equality of the straight line 

Conical section coulter with a common apex and a common half parameter
Ellipse with orthoptic curve (purple)
Ellipse: Pole-Polar Relationship
Focal Point Property
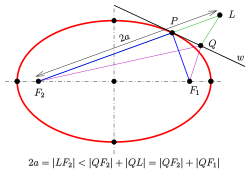
The tangent bisects the exterior angle of the focal rays
Ellipse with guidelines
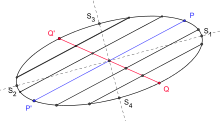
Ellipse with two conjugate diameters
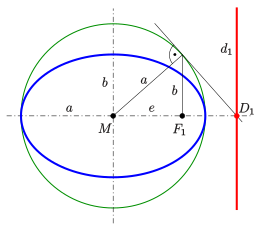
Guideline construction
Ellipse as affine image of the unit circle
Another definition of the ellipse uses a special geometric mapping, namely affinity. Here the ellipse is defined as an affine image of the unit circle.
Parameter representation
An affine mapping in the real plane is of the form 










Vertex, vertex shape
Since in a vertex the tangent is perpendicular to the associated ellipse diameter and the tangent direction in an ellipse point is 

and thus from 
(The formulas
were 
If 

The 4 vertices of the ellipse are
The vertex shape of the parameter representation of the ellipse is
Semi-axes
With the abbreviations 
If we solve for 
Area
From the second theorem of Apollonios follows:
The area of an ellipse 
For example 3,
Examples
provides the usual parameter representation of the ellipse with the equation
.
gives the parameter representation of the ellipse, which
arises from
by rotating it by angle φ
and then shifting it by The parameter representation is already in vertex form. That is,
and
are the vertices of the ellipse.
- The parameter representation
of an ellipse is not in vertex form.
The vertex parameter is given by 

The vertex form of the parameter representation is:
The vertices are: 
the semi-axes:
Implicit representation
Solving the parameter representation using Cramer's rule for 


For example 3 we get:
If we rotate the ellipse with the equation 

Conversely, if the equation of a rotated ellipse is present and one wants to take advantage of the parameter representation described here, one determines the position vectors of two conjugate points. If one chooses as first point 
Example: For the ellipse with the equation 
the position vectors of two conjugate points.
Ellipse in space
If the vectors are 

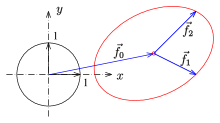
Ellipse as affine image of the unit circle
Transformation to vertex shape (example 3)
Sequence of ellipses: rotated and scaled so that two consecutive ellipses touch each other.
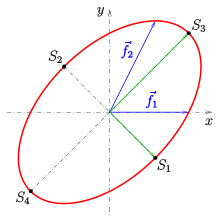
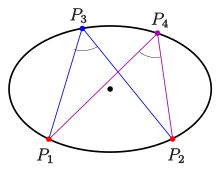
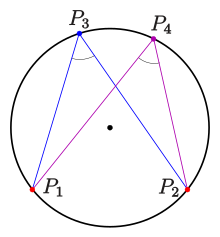
Peripheral angle theorem and 3-point form for ellipses
Circles
A circle with equation 


Four points 


Usually one measures an inscribed angle in degrees or radians. To determine the equation of a circle through 3 points, the following angle measure is more suitable:
To measure the angle between two straight lines with equations 
This quotient is the cotangent of the intersection angle of the two straight lines.
Peripheral angle theorem for circles:For four points 
The four points lie on a circle exactly when the angles at 

The angle measure is initially available only for secants that are not parallel to the 
A consequence of the Peripheral Angle Theorem in this form is:
3-point form of a circular equation:
The equation of the circle through the 3 points 
This formula can be written more clearly by using the position vectors, the scalar product and the determinant:
Example:
For 

Ellipses
In this section only ellipses are considered with equations
for which the quotient 


The axes of such ellipses are parallel to the coordinate axes and their eccentricity (see above) is fixed. The major axis is parallel to the 


As with the circle, such an ellipse is not uniquely determined by three points on a straight line.
For this more general case, one introduces the following angular measure:
To measure the angle between two straight lines with equations 
Peripheral Angle Theorem for Ellipses:
For four points 
The four points lie exactly on an ellipse with the equation 


The angle measure is initially available only for secants that are not parallel to the 
The proof results from simple recalculation. In the case "points on an ellipse ..." one can assume that the center of the ellipse is the origin.
A consequence of the Peripheral Angle Theorem in this form is:
3-Point Form of an Ellipse Equation:
The equation of the ellipse through the 3 points 
This formula can be represented more clearly (as with the circle) by
where ∗ 
Example:
For 



Ellipse: Peripheral Angle Theorem
Circle: Peripheral Angle Theorem
Examples
- If you look obliquely at a circle (for example, at the top surface of a circular cylinder), this circle appears as an ellipse; more precisely, a parallel projection generally maps circles onto ellipses.
- In astronomy, ellipses often occur as orbits of celestial bodies. According to Kepler's first law, every planet moves on an ellipse around the sun, with the sun resting in one of the two foci. The same is true for the orbits of recurrent (periodic) comets, planetary moons or double stars. In general, every two-body problem of gravitational force results in elliptical, parabolic or hyperbolic orbits, depending on the energy.
· 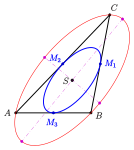
Steiner ellipse (blue) with Steiner ellipse (red)
· 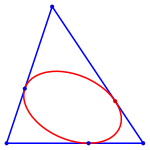
Example of an Inellipse
- For every two- or three-dimensional harmonic oscillator, the motion occurs on an elliptical path. For example, the pendulum bob of a thread pendulum oscillates approximately on an elliptical path, if the motion of the pendulum thread is not only in one plane.
- In triangle geometry there are Steiner ellipses, inellipses (Steiner ellipse, Mandart ellipse).
Collection of formulas (elliptic equations)
Ellipse equation (Cartesian coordinates)
center 
Resolved to 
The last form is convenient for representing an ellipse using the two orbital elements, numerical eccentricity and major semi-axis.
Center 

Ellipse equation (parameter form)
Center 

Center 

Center 

Here 






For non-rotated ellipses, i.e. α 

This relation allows an illustrative interpretation of the parameter 








Ellipse equation (polar coordinates with respect to the center)
Main axis horizontal, center as pole, polar axis along main axis to the right:
Expressed in Cartesian coordinates, parameterized by the angle of the polar coordinates, with the center of the ellipse at 

Derivation
From the ellipse equation in Cartesian coordinates 


Rearrange and square root gives the radius depending on the polar angle.
Ellipse equation (polar coordinates with respect to a focal point)
Main axis horizontal, right focal point as pole, polar axis along main axis to the right (half parameter 
Main axis horizontal, left focal point as pole, polar axis along main axis to the right:
The range of values of the radii extends from the periapsis distance 

Expressed in Cartesian coordinates, parameterized by the angle φ 



The angle φ 

Derivation
Consider a triangle formed by the two fixed points 


The distances between these points are: 




The derivation for the right pole is analogous. The distances are 






Alternative derivation
By equating the two representations of 
This corresponds on the one hand with 
and on the other hand with 

Formula collection (curve properties)
Tangent equation (Cartesian coordinates)
Center 


Center 


Tangent equation (parameter form)
An (unnormalized) tangent vector to the ellipse has the shape:
The tangent equation in vectorial representation with center at 


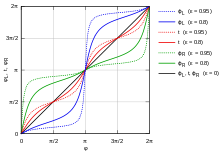
Relationship between polar angle and normal angle
There 


Derivation
The relation of the polar angle φ 

Solving the tangent equation to
gives the tangent slope 

With 


Normal equation (Cartesian coordinates)
Center 


or also
Normal equation (parameter form)
An (unnormalized) normal vector to the ellipse has the shape:
The normal equation in vectorial representation with center at 


Radii and centers of curvature
Radius of curvature at point 
Center of the circle of curvature, center of curvature 
Radius and center of curvature in one of the two principal vertices 
Radius and center of curvature in one of the two minor vertices 
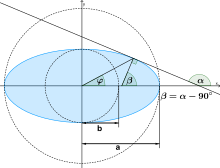
The angles of the elliptic tangent
Formula collection (area and perimeter)
Area
With semiaxes 

If the ellipse is given by an implicit equation
then its area is
Ellipse sector
For an ellipse with semiaxes 

![{\displaystyle \varphi \in \left]0,{\frac {\pi }{2}}\right[}](https://www.alegsaonline.com/image/88eaaad47eb1f3411844f2b0b60113462511a4c0.svg)
If one describes the ellipse sector instead of the polar angle by the parameter 

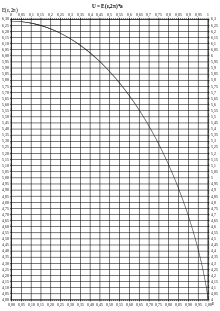
Scope
Formula
The circumference 



where 


Derivation
The circumference 
The formula for the arc length of a 


For the ellipse with parameter representation taking into account the symmetry for the perimeter U, we get {\displaystyle

Factoring out 


By substituting 

The integral 
The circumference 

The circumference 









Series development
For ε 
A series that converges faster is based on the Gauss-Kummer series. For an ellipse with semi-axes 



Approximations
Approximation using the arithmetic mean of the semi-axes
Accuracy of this formula
| Exc. ε | q = b / a | Error |
| = 0,000 | 1,000 | 0 (circle: exact) |
| < 0,051 | > 0,9987 | < 10−7 |
| < 0,090 | > 0,996 | < 10−6 |
| < 0,1582 | > 0,9874 | < 10−5 |
| < 0,277 | > 0,961 | < 0,01 % |
| < 0,46 | > 0,885 | < 0,1 % |
| < 0,75 | > 0,66 | < 1 % |
| < 0,83 | > 0,55 | < 2 % |
| < 0,927 | > 0,37 | < 5 % |
| < 0,978 | > 0,21 | < 10 % |
| < 0,999 | > 0,044 | < 18,3 % |
| < 1,000 | > 0,000 | < 21,46 % |
Approximation using the root mean square of the semi-axes
Accuracy of this formula
| Exc. ε | q = b / a | Error |
| = 0,000 | = 1,0000 | 0 (circle: exact) |
| < 0,016 | > 0,9999 | < 10−9 |
| < 0,026 | > 0,9997 | < 10−8 |
| < 0,047 | > 0,9989 | < 10−7 |
| < 0,084 | > 0,9965 | < 10−6 |
| < 0,149 | > 0,9888 | < 10−5 |
| < 0,262 | > 0,9651 | < 0,01 % |
| < 0,450 | > 0,8930 | < 0,1 % |
| < 0,720 | > 0,6937 | < 1 % |
| < 0,808 | > 0,5891 | < 2 % |
| < 0,914 | > 0,4037 | < 5 % |
| < 0,977 | > 0,2104 | < 10 % |
| < 1,000 | > 0,0000 | < 14,91 % |
Approximation formula according to Ramanujan
respectively


This approximation is very accurate in a wide ε 


The relative error is:
| Area | rel. Error |
| 0,0000 ≤ ε ≤ 0,8820 | < 10−9 |
| 0,8820 < ε ≤ 0,9242 | < 10−8 |
| 0,9242 < ε ≤ 0,9577 | < 10−7 |
| 0,9577 < ε ≤ 0,9812 | < 10−6 |
| 0,9812 < ε ≤ 0,9944 | < 10−5 |
| 0,9944 < ε ≤ 0,9995 | < 10−4 |
| 0,9995 < ε ≤ 1,0000 | < 0,000403 |
For ε 

See also: Meridian Arc
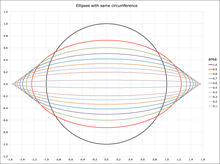
Ellipses with equal perimeter
Character
![]()
Unicode contains four ellipsis symbols in the Miscellaneous Symbols and Arrows block, which can be used as graphic characters or decorative characters in any text (including continuous text):
| Unicode | Characters | Name | LaTeX |
| U+2B2C | ⬬ | black horizontal ellipse (Full horizontal ellipse) |
|
| U+2B2D | ⬭ | white horizontal ellipse (Hollow horizontal ellipse) |
|
| U+2B2E | ⬮ | black vertical ellipse (Full vertical ellipse) | Note |
| U+2B2F | ⬯ | white vertical ellipse (Hollow vertical ellipse) | Note |
Note By rotating the horizontal variant using the package rotating, which is preinstalled with the usual LaTeX distributions.
LaTeX also knows a hollow horizontal ellipse with shadow on the right: \EllipseShadow.
See also
- Steiner ellipse
- Confocal conic sections
- Gabriel Lamé generalized the ellipse to the Lamé curve (superellipse).
- Ellipsoid
- The body of revolution with an elliptical cross-section is an ellipsoid of revolution.
- Homeoid
- Focaloid
- Feynman's lost lecture: The motion of the planets around the sun
- Medium movement
Questions and Answers
Q: What is an ellipse?
A: An ellipse is a shape that looks like an oval or a flattened circle. In geometry, it is a plane curve which results from the intersection of a cone by a plane in a way that produces a closed curve.
Q: How does one create an ellipse?
A: An ellipse can be made by putting two pins into cardboard and then looping string around those two pins and putting a pencil in the loop and pulling as far as possible without breaking the string in all directions.
Q: What are circles special cases of?
A: Circles are special cases of ellipses, created when the cutting plane is perpendicular to the cone's axis.
Q: How many foci does an ellipse have?
A: An ellipse has two foci.
Q: What equation describes an ellipse?
A: The equation for an ellipse is (x - h)²/a² + (y - k)²/b² = 1 where h and k represent the center of the ellipse and 2a represents the length from each end of the longer skinnier side, while 2b represents the length between each end of its shorter side. C represents the length between its foci and center, such that A²-B²=C².
Q: Where do we see examples of elliptical orbits?
A: Elliptical orbits can be seen in planets, with their sun at one focus point.
Search within the encyclopedia









































































![{\displaystyle r(\varphi )={\frac {ab}{\sqrt {a^{2}\sin ^{2}\varphi +b^{2}\cos ^{2}\varphi }}}={\frac {b}{\sqrt {1-\varepsilon ^{2}\cos ^{2}\varphi }}}\in [b,a]\quad {\text{mit}}\quad 0\leq \varphi <2\pi }](https://www.alegsaonline.com/image/c8dc6a96d5f39639f62b3e38193d29508b588b9e.svg)


![r_{\mathrm {R} }(\varphi _{\mathrm {R} })={\frac {a^{2}-e^{2}}{a+e\cos \varphi _{\mathrm {R} }}}={\frac {p}{1+\varepsilon \cos \varphi _{\mathrm {R} }}}\in [r_{\mathrm {peri} },r_{\mathrm {apo} }]\quad {\text{mit}}\quad 0\leq \varphi _{\mathrm {R} }<2\pi](https://www.alegsaonline.com/image/bfa9c4f788d7c2b53d3f7a8d8b5d7ca0bbb85f10.svg)
![r_{\mathrm {L} }(\varphi _{\mathrm {L} })={\frac {a^{2}-e^{2}}{a-e\cos \varphi _{\mathrm {L} }}}={\frac {p}{1-\varepsilon \cos \varphi _{\mathrm {L} }}}\in [r_{\mathrm {peri} },r_{\mathrm {apo} }]\quad {\text{mit}}\quad 0\leq \varphi _{\mathrm {L} }<2\pi](https://www.alegsaonline.com/image/1270348737b4303ae3564fde78beba3463dc019d.svg)





![\left.{\begin{array}{l}r_{\mathrm {L} }^{2}-r_{\mathrm {R} }^{2}=\left[y^{2}+(x+e)^{2}\right]-\left[y^{2}+(x-e)^{2}\right]=4ex=4a\varepsilon x\\r_{\mathrm {L} }^{2}-r_{\mathrm {R} }^{2}=(r_{\mathrm {L} }+r_{\mathrm {R} })(r_{\mathrm {L} }-r_{\mathrm {R} })=2a(r_{\mathrm {L} }-r_{\mathrm {R} })\end{array}}\right\}\implies r_{\mathrm {L} }-r_{\mathrm {R} }=2\varepsilon x](https://www.alegsaonline.com/image/8448d8fb13596dfb513a2aef5aeff3b53e09969f.svg)




























![{\begin{aligned}U&=2a\pi \left(1-\sum _{i=1}^{\infty }\left(\prod _{j=1}^{i}{\frac {2j-1}{2j}}\right)^{2}{\frac {\varepsilon ^{2i}}{2i-1}}\right)\\&=2a\pi \left[1-\left({\frac {1}{2}}\right)^{2}\varepsilon ^{2}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {\varepsilon ^{4}}{3}}-\ldots -\left({\frac {1\cdot 3\cdot 5\dotsm (2n-1)}{2\cdot 4\cdot 6\dotsm 2n}}\right)^{2}{\frac {\varepsilon ^{2n}}{2n-1}}-\ldots \right]\end{aligned}}](https://www.alegsaonline.com/image/d72543ea500e05b263cce5a6a6aa62832841990b.svg)